Workgroup 4: Deriving Selection Rules with Symmetry
- Page ID
- 56051
Name: ______________________________
Section: _____________________________
Student ID#:__________________________
In chemistry and physics, selection rules define the transition probability from one eigenstate to another eigenstate. In this Workgroup activity, we are going to discuss the transition moment, which is the key to understanding the intrinsic transition probabilities. Selection rules have been divided into the electronic spectroscopy, vibrational spectroscopy, and rotational spectroscopy.
Transition Moment Integrals Couple Eigenstates
In an atom or molecule, an electromagnetic wave (for example, visible light) can induce an oscillating electric or magnetic moment. The amplitude of this (electric or magnetic) moment is called the transition moment and the probability of promoting (or demoting) a molecule from one eigenstate \(|Ψ_1 \rangle \) to a different eigenstate \(|Ψ_2 \rangle \) is given by |\(\vec{M}_{21}|^2\), and \(\vec{M}_{21}\) is called the transition dipole moment, or transition moment, from \(|Ψ_1 \rangle \) to \(|Ψ_ 2 \rangle \):
\[\vec{M}_{21}= \langle \Psi_2 | \vec{\mu} | \Psi_1 \rangle \tag{transition moment integral}\]
where \(\vec{M}_{21}\) is the electric dipole moment operator. If we have a system with \(n\) particles with charge \(q_n\), and the electric dipole moment operator:
\[ \vec{\mu}=\sum_{n}q_n\vec{x}_n \tag{electric dipole moment operator}\]
the \(\vec{x}_{n}\) is the position vector operator.
- If \(| \vec{M}_{21} |\) is big, then the transition has a high probability of occurring (i.e., observing in a spectrum)
- If \(| \vec{M}_{21} |\) is small, then the transition has a weak probability of occurring (i.e., observing in a spectrum)
- If \(| \vec{M}_{21} |\) is zero, then the transition has a zero probability of occurring (i.e., observing in a spectrum)
Symmetry to the Rescue
To evaluate \(| \vec{M}_{21} |\), we need to know the functional forms of \(|Ψ_1 \rangle \), \(|Ψ_ 2 \rangle \), and \(\vec{\mu} \), which results in a difficult integral to numerically or analytically solve. However, symmetry can be used to consider if \(| \vec{M}_{21} |\) may be zero.
Microwave Spectroscopy Selection Rules
The solutions to the rigid rotor Schrödinger equation are spherical harmonic functions (see Table M4).
\[ | \psi _{l, m_l } (\theta , \phi) \rangle = Y^{m_l}_l (\theta , \phi)\]
These depend upon the two variables \(\theta\), and \(\phi \) with two quantum numbers \(l\), and \(m_l\). These are the angular part of atomic orbitals that have been discussed before (see below).
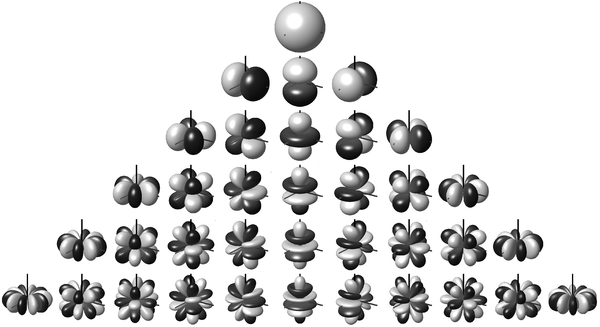
Q1
Evaluate this integral
\[ \langle Y^{m_l'}_{l'} (\theta , \phi) | Y^{m_l}_l (\theta , \phi) \rangle \]
- if \(m_l' \neq m_l\) or \(l' \neq l\)?
- if \(m_l' = m_l\) and \(l' = l\)?
Q2
Vibrational Spectroscopy Selection Rules
The harmonic oscillator wavefunctions are
\[ | \psi(r) \rangle = N_vH_v(\alpha^{1/2}r) e^{-\alpha r^2/2}\]
where Hv(a1/2q) is a Hermite polynomial and a = (km/á2)1/2.

