Workgroup 2: Symmetry and Assigning Point Groups
- Page ID
- 62456
Name: ______________________________
Section: _____________________________
Student ID#:__________________________
Separate into groups of five-eight students and answer the following questions. You will be graded primarily on effort, not accuracy (although if all questions are incorrect, then the effort is clearly missing). It is OK to use external resources such as textbooks and websites. It is not ok to copy word-for-word the solution. Each group must come up with their answers collectively and without plagiarism of existing resources.
The symmetry properties of objects (and molecules) may be described in terms of the presence of certain symmetry elements and their associated symmetry operations. Each molecule has a set of symmetry operations that describes the molecule's overall symmetry. This set of operations define the point group of the molecule. The process used to assign a molecule to a point group is straightforward with a few exceptions and follows three major steps:
- Identify the geometry of the typically with the standard VSEPR approach learned in General Chemistry
- Identify the symmetry elements of the molecule in that geometry
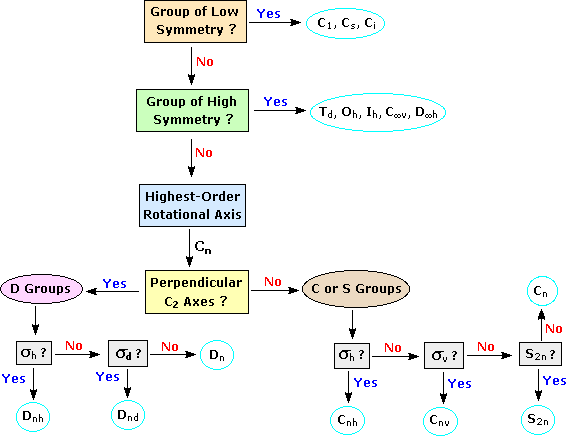
- Follow the flowchart below to determine flow chart (often step 2 can be done via step 3).
Here are set of steps to quickly guide you (with flowchart).
- Look at the molecule and see if it seems to be very symmetric or very unsymmetric. If so, it probably belongs to one of the special groups (low symmetry: \(C_1\), \(C_s\), \(C_i\) or linear \(C_{∞v}\), \(D_{∞h}\)) or high symmetry (\(T_d\), \(O_h\), \(I_h\)..).
- For all other molecules find the rotation axis with the highest n, the highest order \(C_n\) axis of the molecule.
- Does the molecule have any \(C_2\) axes perpendicular to the \(C_n\) axis? If it does, there will be n of such \(C_2\) axes, and the molecule is in one of D point groups. If not, it will be in one of \(C\) or \(S\) point groups.
- Does it have any mirror plane (\(σ_h\)) perpendicular to the \(C_n\) axis? If so, it is \(C_{nh}\) or \(D_{nh}\).
- Does it have any mirror plane (\(σ_d\), \(σ_v\))? If so, it is \(C_{nv}\) or \(D_{nd}\).
Below is the standard flow chart that graphical displays the above steps to assign point groups
Q1
Draw sketches to identify the following symmetry elements:
- a \(C_3\) axis and a \(σ_v\) plane in the \(NH_3\) molecule;
- a \(C_4\) axis and a \(σ_h\) plane in the square planar \([PtCl_4]^{2–}\) ion
Q2
For each of the following molecules and ions, identify if it has a center of inversion (i) and/or a \(S_4\) axis and indicate either on a plot of the molecule:
- \(CO_2\)
- \(C_2H_2 \;(acetylene)\)
- \(BF_3\)
- \(SO_4^{2–}\)
Q3
If you have a computer available, go to Otterbein's symmetry website (symmetry.otterbein.edu/challenge/index.html) and click on ammonia (half way down the left "molecule" list. Proceed through the flowchart shown question by question on the right side to identify the point group. If computer is not available, then use the flowchart above.
Q4
What is the definition of a polar molecule? Use examples of polar molecules to identify if a polar molecule has one or more of the primary symmetry elements:
- a proper rotation axis
- a center of inversion
- an improper rotational axis
- a mirror plane
In terms of point groups, only molecules that are polar are those in the \(C_n\), \(C_{nv}\), and \(C_s\) point groups.
Q5
What is the definition of a chiral molecule? Use examples of chiral molecules to identify if a chiral molecule has one or more of the primary symmetry elements:
- a proper rotation axis
- a center of inversion
- an improper rotational axis
- a mirror plane
In terms of point groups, the only chiral point groups are \(C_n\) and \(D_n\). Can a molecule be both polar and chiral?
Q4
Determine the symmetry elements and assign the point group of the following molecules. Also indicate if the molecule is polar and if the molecule chiral.
| Molecule | Symmetry elements (just labels, not diagrams) | Point Group | Polar (Yes/no) | Chiral (yes/no) |
|---|---|---|---|---|
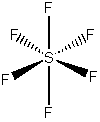
| \(SF_6\) | ||||
| \(CCl_4\) | ||||
| \(\ce{H_2C=CH_2}\) | ||||
| \(\ce{H_2C=CF_2}\) | ||||
 |
||||
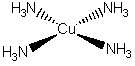 |
Q5
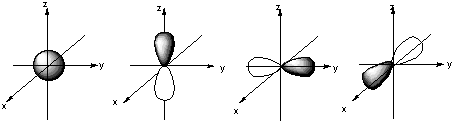
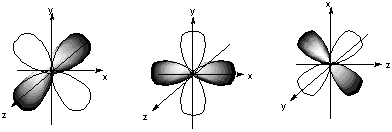
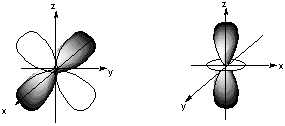
- Classify these nine atomic orbitals by their symmetry under inversion, that is, by their change in a center of symmetry. Which of these atomic orbitals are even (do not change sign) and which are odd (do change sign) under inversion?
- B. Consider a py atomic orbital on one nuclear center A and one of the five d atomic orbitals on another nuclear center B. Let the nuclear centers A and B be placed on the x axis with A on the left and B on the right. As A and B approach, molecular orbitals can be formed from the two atomic orbitals if these two atomic orbitals have the same symmetry with respect tot he internuclear axis. With which atomic d orbital on B is there a nonzero (noncancelling) overlap with the atomic py orbital on A?
- Draw pictures of the bonding and anitbonding molecular orbitals that result from this linear combination of atomic orbitals.
- Classify the resulting molecular orbital as to its symmetry with respect to the internuclear axis.

