18.7: The Vibrational Partition Function
- Page ID
- 51130
As with diatomic molecules, the energies of polyatomic molecules can be approximated by the sum of its individual degrees of freedom. Therefore, we can write the partition function as:
\[ Q(N,V,T) = \frac{[q(V,T)]^2}{N!} \]
We can write the polyatomic analog to diatomic molecules:
\[ Q(N,V,T) = \frac{(q_\text{trans}q_\text{rot}q_\text{vib}q_\text{elec})^N}{N!} \]
When derived for diatomic molecules, we assumed the rigid rotor model for rotations and the harmonic oscillator for vibrations. This allowed us to separate the rotational motion from the vibrational motion of the molecule. Polyatomic molecules are a bit more complicated, but we will still make use of these approximations.
The number of translational states available to any given molecule is far greater than the number of molecules in the system. \(q_\text{trans}\) is given by:
\[ q_\text{trans} = \left[\frac{2\pi MkT}{h^2}\right]^{3/2}V \]
where \(M\) is the mass of the particle. Moving to the electronic partition function:
\[ q_\text{elec} = \sum_i{g_{i}e^{-E_i/kT}} \]
where \(E_i\) is the energy of the electronic state \(i\) and {g_i} is its degeneracy. Electronic states are typically spaced far apart from each other. The probability of the system being in any state but the ground state is extremely small. We can therefore simplify the electronic partition function to include only the ground electronic state:
\[ q_\text{elec} = g_{e1}e^{D_e/kT} \]
where \(-D_e\) is the energy of the ground electronic state. To complete the polyatomic partition function, we still need \(q_\text{vib}\) and \(q_\text{rot}\). We will finish this section with \(q_\text{vib}\) and talk about \(q_\text{rot}\) in the next.
The vibrational motion of diatomic molecules can be expressed as a set of independent harmonic oscillators. For polyatomic molecules, the independent vibrational motions are referred to as normal modes of vibration. The vibrational energy is then the sum of the energies for each normal mode:
\[ E_\text{vib} = \sum_i^\alpha{\left(v_i + \frac{1}{2}\right)h\nu} \]
where \(\nu_i\) is the vibrational frequency for the \(i\)th normal mode and \(\alpha\) is the number of vibration degrees of freedom. A linear molecule has \(3n-5\) vibrational degrees of freedom and a nonlinear molecule has \(3n-6\) vibrational degrees of freedom. Because the normal modes are independent of each other, we can take out results from previous sections:
\[ q_\text{vib} = \prod_i^\alpha{\frac{e^{-\theta_{\text{vib},i}/2T}}{1-e^{-\theta_{\text{vib},i}/T}}} \]
\[ E_\text{vib} = Nk \sum_i^\alpha{\left( \frac{\theta_{\text{vib},i}}{2} + \theta_{\text{vib},i} \frac{e^{-\theta_{\text{vib},i}/T}}{1-e^{-\theta_{\text{vib},i}/T}} \right)} \]
\[ C_{V,\text{vib}} = Nk \sum_i^\alpha{\left( \left(\frac{\theta_{\text{vib},i}}{2}\right)^2 + \frac{e^{-\theta_{\text{vib},i}/T}}{(1-e^{-\theta_{\text{vib},i}/T})^2} \right)} \]
where \(\theta_{\text{vib},i}\) is the characteristic vibrational temperature defined by:
\[ \theta_{\text{vib},i} =\frac{h\nu_i}{k} \]
Vibrational Entropy
There is a great deal of utility for thermodynamic functions calculated from the vibrational normal modes of a molecule. The vibrational energy and entropy depend on the shape a multidimensional potential energy surface. If one performs a conformational search of macromolecule it is one obtains energies and structures but little direct information concerning the shape of the potential energy surface for each conformation. The vibrational entropy gives a means determining whether there are significant entropic differences in the structures and therefore whether certain conformations will be favored based on the entropy.
However, it is possible to take appropriate linear combinations of the coordinates so that the cross terms are eliminated and the classical Hamiltonian as well as the operator corresponding to it contains no cross terms and in terms of the new coordinates, the Hamiltonian can be written as,
\[ H = \sum_{i=1}^{f} \dfrac{h^2}{2 \mu_i} \dfrac{\partial}{\partial q_i^2}+ \sum_{i=1}^{f} \dfrac{k_i}{2} q_i^2 \label{3.81} \]
Here, the degrees of freedom \(f\) is \(3N - 5\) for a linear molecule and \(3N - 6\) for a nonlinear molecule. Here, \(k_i\) is the force constant and \(μ_i\) is the reduced mass for that particular vibrational mode which is referred to as a normal mode.
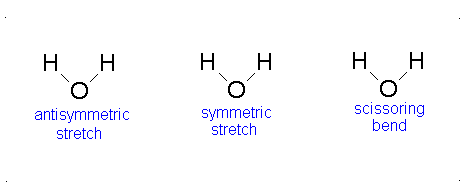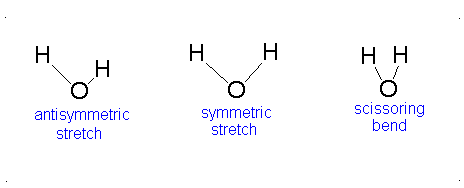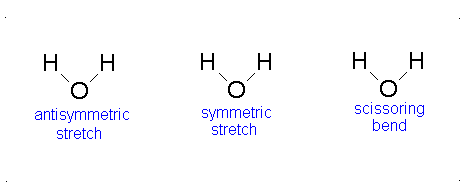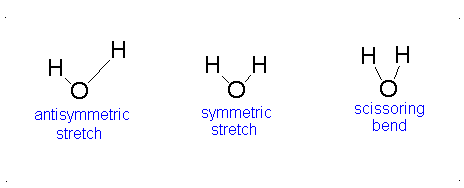
The Equation \(\ref{3.81}\) represents \(f\) linearly independent harmonic oscillators and the total energy for such a system is
\[ \epsilon_{vib} = \sum_{i=1}^{f} \left( v_i + \dfrac{1}{2} \right) h \nu_i \nonumber \]
The vibrational frequencies are given by
\[ \nu_i = \dfrac{1}{2 \pi} \sqrt{\dfrac{k_i}{\mu_i}} \nonumber \]
The vibrational partition function is given by the product of \(f\) vibrational functions for each frequency.
\[ q_{vib} = \prod_{i=1}^f \dfrac{ e^{-\Theta_{vib,i}/2T} }{1- e^{-\Theta_{vib,i}/T}} \label{Qvib1} \]
with
\[ \Theta_{vib,i} = \dfrac{h\nu_i}{k_B} \nonumber \]
As with the previous discussion regarding simple diatomics, \(\Theta_{vib,i}\) is called the characteristic vibrational temperature. The molar energies and the heat capacities are given by
\[ \langle E_{vib} \rangle = Nk \sum_{i=1}^f \left[ \dfrac{ \Theta_{vib,i} }{2} + \dfrac{ \Theta_{vib,i} e^{-\Theta_{vib,i}/T} }{1- e^{-\Theta_{vib,i}/T}} \right] \nonumber \]
and
\[ \bar{C}_V = Nk_B \sum_{i=1}^f \left( \dfrac{ \Theta_{vib,i} }{T} \right)^2 \dfrac{ e^{-\Theta_{vib,i}/T} }{\left(1- e^{-\Theta_{vib,i}/T}\right)^2} \nonumber \]
The three characteristic vibrational temperatures for \(\ce{NO2}\) are 1900 K, 1980 K and 2330 K. Calculate the vibrational partition function at 300 K.
Solution
The vibrational partition is (Equation \(\ref{Qvib1}\))
\[ q_{vib} = \prod_{i=1}^f \dfrac{ e^{-\Theta_{vib,i}/2T} }{1- e^{-\Theta_{vib,i}/T}} \nonumber \]
If we calculate \(q_{vib}\) by taking the zero point energies as the reference points with respect to which the other energies are measured
\[\begin{align*} q_{vib} &= \prod_{i=1}^f \dfrac{ 1 }{1- e^{-\Theta_{vib,i}/T}} = \left( \dfrac{ 1 }{1- e^{-1900/300}} \right) \left( \dfrac{ 1 }{1- e^{-1980/300}} \right) \left( \dfrac{ 1 }{1- e^{-2330/300}} \right) \\[4pt] & =(1.0018) ( 1.0014)(1.0004) = 1.0035 \end{align*} \nonumber \]
The implication is that very few vibrational states of \(\ce{NO2}\) (other than the ground vibrational state) are accessible at 300 K. This is standard of the vibrations of most molecules.
Contributors and Attributions
- www.chem.iitb.ac.in/~bltembe/pdfs/ch_3.pdf

