18.4: Most Molecules Are in the Ground Vibrational State at Room Temperature
- Page ID
- 51127
The vibrational energy levels of a diatomic are given by:
\[E_v = (v +1/2) h \nu \]
where is \(\nu\) the vibrational frequency and \(v\) is the vibrational quantum number. In this case, it is easy to sum the geometric series shown below:
\[\begin{align*} q_\text{vib} &= \sum_{v=0}^{\infty} e^{-( v + 1/2) h\nu / k T} \\[4pt] &= e^{-h \nu/ 2kT} \left( 1 + e^{-h \nu/ 2kT} + e^{-2 h \nu/ 2kT} + ... \right) \end{align*} \nonumber \]
or rewritten as:
\[ q_\text{vib} = e^{-h \nu / 2kT} \left( 1 +x + x^2 +x^3 + ... \right) \label{eq0} \]
where \(x = e^{-h \nu/kT} \). Given the following power series expansion:
\[ \dfrac{1}{1 - x} = 1 + x + x^2 + x^3 + x^4 + .... \nonumber \]
Equation \(\ref{eq0}\) can be rewritten as:
\[ q_\text{vib} = e^{-h \nu / 2kT} \left( \dfrac{1}{1-x} \right) \nonumber \]
or:
\[q_\text{vib} = \dfrac{e^{-h \nu / 2 k T}} {1 - e^{-h \nu/ k T}} \label{eq1} \]
If the zero of energy scale is at \(h \nu /2kT\), then Equation \(\ref{eq1}\) can be rewritten as:
\[q_\text{vib} \approx \dfrac{1} {1 - e^{-h \nu / kT}} \label{VIBQ} \]
A vibrational temperature \(Θ_\text{vib}\) may be defined as:
\[ Θ_\text{vib}= \dfrac{ hc \tilde{\nu}}{k} \nonumber \]
where \(\tilde{\nu}\) is the vibrational frequency in cm-1. \(Θ_\text{vib}\) is a good way to express the stiffness of the vibrating bond in units of the Boltzmann constant. Because the stiffness obviously depends on what bond your are talking about, this is a good way to do the same thing we did for the critical temperature of the non-ideal gases.
| Molecule | g | Bond Length (pm) | \(ω\) (cm-1) | \(Θ_\text{vib}\) (K) | \(\tilde{B}\) (cm-1) | \(Θ_\text{rot}\) (K) | Force constant \(k\) (dynes/cm) | \(D_0\) (kcal/ mol) |
|---|---|---|---|---|---|---|---|---|
| \(H_2\) | 1 | 0.7474 | 4400 | 6332 | 60.9 | 87.6 | 5.749 | 103.2 |
| \(D_2\) | 1 | 0.7415 | 3118 | 4487 | 30.45 | 43.8 | 5.77 | 104.6 |
| \(N_2\) | 1 | 1.097 | 2358 | 3393 | 2.001 | 2.99 | 22.94 | 225.1 |
| \(O_2\) | 3 | 1.207 | 1580 | 2274 | 1.446 | 2.08 | 11.76 | 118.0 |
| \(Cl_2\) | 1 | 1.987 | 560 | 805 | 0.244 | 0.351 | 3.2 | 57.0 |
| \(CO\) | 1 | 1.128 | 2170 | 3122 | 1.931 | 2.78 | 19.03 | 255.8 |
| \(NO\) | 2 | 1.15 | 190 | 2719 | 1.695 | 2.45 | 15.7 | 150.0 |
| \(HCl\) | 1 | 1.275 | 2938 | 4227 | 10.44 | 15.02 | 4.9 | 102.2 |
| \(HI\) | 1 | 1.609 | 2270 | 3266 | 6.46 | 9.06 | 3.0 | 70.5 |
| \(Na_2\) | 1 | 3.096 | 159 | 229 | 0.154 | 0.221 | 0.17 | 17.3 |
| \(K_2\) | 1 | 3.979 | 92.3 | 133 | 0.0561 | 0.081 | 0.10 | 11.8 |
The vibrational frequency of of \(I_2\) is \(214.57\; cm^{-1}\). Calculate the vibrational partition function of \(I_2\) at 300 K.
Solution:
\[\dfrac{h\nu}{kT} = \dfrac{ 214.57}{209.7} = 1.0232 \nonumber \]
so
\[e^{-h\nu/kT} = 0.3595 \nonumber \]
and
\[q_\text{vib} = \dfrac{1}{1-0.3595} = 1.561 \nonumber \nonumber \]
This implies, as before, that very few vibrational states are accessible and much less than rotation states and many orders less than translation states.
Vibrational Heat Capacity
The vibrational energy is given by the above expression and the molar heat capacity at constant volume, \(\bar{C}_V\) is given by:
\[ \bar{C}_V= \left(\dfrac{\partial E}{\partial T} \right)_V \nonumber \]
We have:
\[ \begin{align} \dfrac{\partial }{\partial T} &= \dfrac{\partial \beta}{\partial T} \dfrac{∂}{\partial \beta} \\[4pt] &= \dfrac{-1}{kT^2} \dfrac{\partial }{\partial \beta} \\[4pt] &= \left(-k \beta^2 \right) \left(\dfrac{\partial }{\partial \beta}\right) \label{3.54} \end{align} \]
Therefore:
\[\bar{C}_V = (-k \beta^2 ) \left(\dfrac{\partial ε_\text{vib}}{\partial \beta}\right) \nonumber \]
and when the vibrational partition function (Equation \(\ref{VIBQ}\)) is introduced:
\[\begin{align} q_\text{vib} &= -k \beta^2 \dfrac{ \left[ (1 - e^{-hc \nu / k T}) (-hc \tilde{\nu}) - e^{-hc \nu / k T} (+ hc\tilde{\nu}) \right] e^{-hc \nu / k T} }{ (1 - e^{-hc \nu / k T})^2 } hv \tilde{\nu} \\[4pt] &= k \left( \dfrac{ Θ_\text{vib} }{T} \right)^2 \dfrac{ e^{- Θ_\text{vib} /T} }{ \left( 1- e^{- Θ_\text{vib}/T} \right)^2 } \label{FinalQ} \end{align} \]
For large \(T\), the \(\bar{C}_V\) becomes:
\[N_A k = R \nonumber \]
and for small T, \(\bar{C}_V\) goes to zero as demonstrated in Figure 18.4.1 .
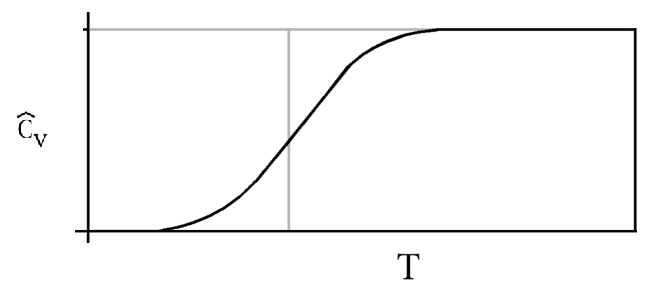
The vibrational heat capacity is shown as function of the reduced temperature \(T/Θ\) to get a general picture valid for all diatomic gases. Compare the parameters on Table 18.4.1 to see on what different absolute scales we have to think for different gases. Clearly the vibrational contribution to the heat capacity depends on temperature. For many molecules (especially light ones), the vibrational contribution only kicks in at quite high temperatures.
The value of \(Θ_\text{vib}\) is determined mostly by
- the strength of a bond (the stronger the higher \(Θ_\text{vib}\) )
- the (effective) mass of the molecule (the lighter the higher \(Θ_\text{vib}\) )
Molecules with low \(Θ_\text{vib}\) often dissociate at lower temperatures, although the harmonic oscillator model is not sufficient to describe that phenomenon.
Vibrational Populations
We can calculate the fraction of molecules in each vibrational state. The fraction of molecules in the \(v\)th vibrational state is given by:
\[ f_v = \frac{e^{-h\nu(v+\frac{1}{2})/kT}}{q_\text{vib}} \]
Substituting in Equation \(\ref{eq1}\), we get:
\[\begin{split} f_v &= \left(1-e^{-h\nu/kT}\right)e^{-h\nu v/kT} \\ &= \left(1-e^{-\Theta_\text{vib}/T}\right)e^{-\Theta_\text{vib} v/T} \end{split} \label{vib1} \]
We can plot the fraction molecules in each vibrational state.
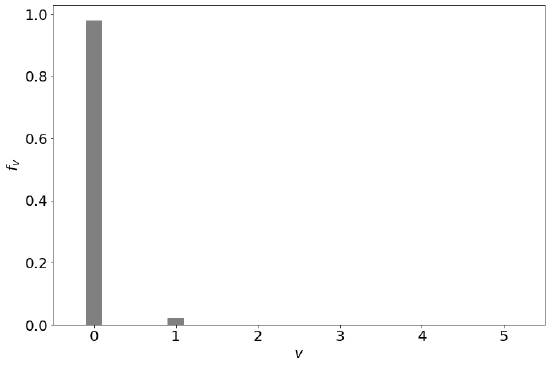
From the figure, we can see that most of the Cl2 molecules are in the ground vibrational state at room temperature (300 K). This is true for most molecules. Only molecules with very weak bonds and low vibrational temperatures will populate a significant fraction of molecules in excited vibrational states.
Contributors and Attributions
- www.chem.iitb.ac.in/~bltembe/pdfs/ch_3.pdf

