13.E: Molecular Spectroscopy (Exercises)
- Page ID
- 51094
These are homework exercises to accompany Chapter 13 of McQuarrie and Simon's "Physical Chemistry: A Molecular Approach" Textmap.
Q13.1
- Calculate the energy difference for radiation wavenumber of, \(\nu=1.00cm^{-1} \) including the type of molecular process that absorbs of this radiation corresponding to.
- Given the wavelength of 3.4 x 10-4, which molecular process does it fall into?
- What are other advantages of knowing the spectroscopy of molecules?
- Do you think the spectroscopy and molecular processes of the molecules have relationship to temperature? Explain.
- What is other form that you can express in above equation?
Q13.20
The vibrational term of a diatomic molecule is
\[ G(v) = (v + \dfrac{1}{2}) \nu_e - (v + \dfrac{1}{2})^2 \chi_e \nu_e \]
Show that the spacing between adjacent levels is given by
\( \Delta G = G(v + 1) - G(v) = \nu_e - 2 \chi_e \nu_e (v+1) \)
Show that the maximum vibrational quantum number, \( v_{max} \) is given by
\[ v_{max} = \dfrac{1}{2\chi_e} - 1 \]
Use this result to show that the dissociation energy of the diatomic molecule can be written as
\[ D_e = \dfrac{\nu_e - \nu_e \chi_e^2}{4\chi_e} \approx \dfrac{\nu_e}{4\chi_e} \]
Explain how the constants \( \nu_e \) and \( \chi_e \) can be evaluated from a plot of \( \Delta G \) versus \( v+1 \), called a Birge-Sponer plot. After finding these constants, determine the dissociation energy of the molecule. Use the following experimental data of \( H_2 \) to determine the dissociation energy of the molecule.
| v | G(v) / cm-1 |
|---|---|
| 0 | 4161.12 |
| 1 | 8087.11 |
| 2 | 11782.35 |
| 3 | 15250.36 |
| 4 | 18497.92 |
| 5 | 21505.65 |
| 6 | 24287.83 |
| 7 | 26830.97 |
| 8 | 29123.93 |
| 9 | 31150.19 |
| 10 | 32886.65 |
| 11 | 34301.83 |
| 12 | 35351.01 |
| 13 | 35972.97 |
Explain why your plot is not linear for high values of \( v \). How does this dissocation energy differ with the experimental value of \( 38269.48 cm^{-1} \).
S13.20
\( \Delta G = G(v + 1) - G(v) = \left(v + \dfrac{3}{2}\right) \nu_e - \left(v + \dfrac{3}{2}\right)^2 \chi_e \nu_e - \left(v + \dfrac{1}{2}\right) \nu_e + \left(v + \dfrac{1}{2}\right)^2 \chi_e \nu_e = \nu_e - \chi_e \nu_e (2v+2) = \nu_e - 2 \chi_e \nu_e (v+1) \)
In the limit that \( \Delta G \rightarrow 0 , v \rightarrow v_{max} \), solving for \( v_{max} \) gives
\[ 0 = \nu_e - 2 \chi_e \nu_e (v_{max}+1) \]
\[ 2\chi_e( v_{max} +1) = 1 \]
\[ v_{max} = \dfrac{1}{2\chi_e} -1 \]
The molecule dissociates in the limit \( \Delta G \rightarrow 0 \), so the dissociation energy is given by
\[ D_e = G(v_{max}) = (\dfrac{1}{2\chi_e} - \dfrac{1}{2}) \nu_e - (\dfrac{1}{2\chi_e} - \dfrac{1}{2})^2 \chi_e \nu_e = \dfrac{\nu_e}{2\chi_e}(1-\chi_e) - \dfrac{\nu_e}{4\chi_e}(1-\chi_e)^2 = \dfrac{\nu_e}{4\chi_e}(2 - 2\chi_e - 1 + 2\chi_e - \chi_e^2) = \dfrac{\nu_e}{4\chi_e}(1 - \chi_e^2) \approx \dfrac{\nu_e}{4\chi_e} \]
The final step can be made if we assume \(\chi_e\) to be very small.
Looking at the equation for \(\Delta G\), we conclude that a plot of \(\Delta G\) versus \( v+1\) will have an intercept of \(\nu_e\) and a slope of \(-2\chi_e\nu_e\). The experimental data points for \(H_2\) can be plotted as such:
If we use a best linear fit, we determine that the intercept is \(\nu_e = 4164.4 cm^{-1} \) and the slope is \( -2\chi_e \nu_e = -232.01 cm^{-1} \). Thus, \( \chi_e = 0.0279 \). Then, the dissociation energy is
\[ D_e = \dfrac{\nu_e}{4\chi_e} = 37400 cm^{-1} \]
The plot is not linear for large values of \(v\) because the potential curve is not well described by the anharmonic potential energy function.
Q13.21
An analysis of the vibrational spectrum of the ground-state homonuclear diatomic molecule \(Na_{2}\) gives \(\tilde{\nu}_{e} = 159.125 \hspace{.1cm}cm^{-1}\) and \(\tilde{\nu}_{e}\tilde{x}_{e} = 0.7255 \hspace{.1cm}cm^{-1}\). Suggest an experimental method that can be used to determine there spectroscopic parameters. Use \(\nu_{max} = \dfrac{1}{2\tilde{x}_{e}}-1\) to determine the number of bound vibrational levels for ground state of \(Na_{2}\).
S13.21
First solve for \(\tilde{x}\):
\[\tilde{x}=\dfrac{0.7255 \hspace{.1cm}cm^{−1}}{159.125\hspace{.1cm}cm^{−1}} = 4.5593 \times 10^{-3} \hspace{.1cm}cm^{−1} \]
Then plug it in to the equation:
\[\nu_{max} = \dfrac{1}{2 \times 4.5593 \times 10^{-3} \hspace{.1cm}cm^{−1}}-1 = 109.67\hspace{.1cm}cm^{−1}\]
There are \(109\) bound vibrational levels for the ground state of \(Ne_{2}\).
Q13.22
A Morse potential is a decent representation of internuclear potential and is modeled by
\[U(q)=D_e(1-e^{-/betaq})^2\]
where \(q=R-R_e\). Prove the force constant for the Morse Potential is evaluated
\[k = 2D_e\beta^2\]
If \(D_e= 6.23\times 10^{-19} J\cdot Molecule^{-1}\) and \(\beta=1.37 \times 10^{10} m^{-1}\) for a given compound, calculate the force constant for that compound.
S13.22
Using a Maclaurin series expansion of the Morse potential, the formula can be rewritten
\[U(q)=D_e(1-e^{-\beta q})^2 = D_e(1-(1-\beta q+\dfrac{\beta^2q^2}{2}O(q)^3))^2 = D_e(\beta^2q^2+O(q)^3)\]
We know that
\[U(q)=\dfrac{kq^2}{2}\]
assuming that \(O(q)^3\) approaches zero, we get
\[\frac{kq^2}{2}= D_e(\beta^2q^2+O(q)^3) \implies k=2D_e\beta^2\]
Plugging in our given values, we get
\[l=2(6.23\times 10^{-19} J\cdot Molecule^{-1})(1.37 \times 10^{10})^2 = 234 N\cdot m^{-1}\]
Q13.23
Given that \(D_{e} = 7.33\times10^{-19} J\cdot molecule^{-1}, \tilde{v}_{e} = 1580.0cm^{-1}, and R_{e} = 121 pm\), find \(k\) and \(\beta\) for \( ^{16}O_{2}\) .
S13.23
Assuming a a harmonic oscillator model, we can use the equation:
\[ \tilde{v}_{e} = \dfrac{1}{2\pi c}\Big(\dfrac{k}{\mu}\Big)^{1/2} \]
We can find \(k\) from the parameters given in the problem. Solving for \(k\) gives
\[ k = (2\pi c\tilde{v}_{e})^{2}\mu\]
\[= [2\pi(3\times10^{10} cm\cdot s^{-1})(1580.0 cm^{-1})]^{2} (7.9975 amu)(1.661x10^{-27} kg\cdot amu^{-1})\]
\[= 1176.3 N\cdot m^{-1}\]
Using the equation:
\[ \beta = \Big(\dfrac{k}{2D_{e}}\Big)^{1/2} \]
We can solve for \(\beta\) using the information above
\[\beta = \Bigg[\dfrac{1176.3N\cdot m^{-1}}{2(7.33\times10^{-19}J)}\Bigg]^{1/2} \]
\[ = 2.84\times10^{10}m^{-1} \]
Q13.24
The fundamental line in the IR spectrum of \(^{12}C^{16}O\) \(cm^{-1}\), and the first overtone occurs at 4260.0 \(cm^{-1}\). Find \(\tilde{v}_{e}\) and \(\tilde{x}_{e}\tilde{v}_{e}\) for \(^{12}C^{16}O\).
S13.24
The equations for the fundamental frequency and the overtone are
\[\tilde{v} = \tilde{v}_{e} - 2\tilde{x}_{e}\tilde{v}_{e}\]
and
\[\tilde{v} = 2\tilde{v}_{e} - 6\tilde{x}_{e}\tilde{v}_{e},\]
respectively.
We can set the fundamental frequency equal to \(2143.0\) \(cm^{-1}\) and the first overtone equal to \(4260.0\) \(cm^{-1}\) which is given from the problem statement. Then, we want to solve for \(\tilde{x}_{e}\tilde{v}_{e}\).
Multiply the fundamental frequency by 3 and subtract the overtone.
\[\tilde{v}_{e} = [3(2143.0) - 4260.0]cm^{-1} = 2169.0 cm^{-1}\]
Then multiply the fundamental frequency by 2 and subtract from the overtone.
\[\tilde{x}_{e}\tilde{v}_{e} = 13.0cm^{-1}\]
Q13.24
Which of the following molecules exhibit a microwave rotational absorption spectrum: BF2,SO2,C2F2,NO3-
S13.24
SO2
notes: microwave rotational absorption correlates to the rotation of polyatomic molecules. Would \(BF_{2}\) and \(NO_{3}^{-}\) also fall in this range?
Q13-25 Slightly Incorrect
Calculate the fundamental and the first two overtones of $$H^{35}Cl$$ given
$$\tilde{v_{e}} = 2990.946 cm^{-1}$$
$$\tilde{x_{e}}\tilde{v_{e}} = 52.819 cm^{-1}$$
S13-25
Use equation, $$\tilde{v_{obs}} = \tilde{v_{e}}\nu -\tilde{x_{e}}\tilde{v_{e}}\nu(\nu+1)$$ with v =1,2...
The fundamental frequency is given by v=1 and the first two overtones are given by v=2 and v=3.
Fundamental: $$\tilde{v_{obs}} = \tilde{v_{e}} -2\tilde{x_{e}}\tilde{v_{e}} = 2990.946cm^{-1} - 2(52.819cm^{-1}) = 2885.308cm^{-1}$$
First overtone:
$$\tilde{v_{obs}} = 2\tilde{v_{e}} -6\tilde{x_{e}}\tilde{v_{e}} = 2990.946cm^{-1} - 6(52.819cm^{-1}) = 5664.978cm^{-1}$$
Second overtone:
$$\tilde{v_{obs}} = 3\tilde{v_{e}} -12\tilde{x_{e}}\tilde{v_{e}} = 3(2990.946cm^{-1}) - 12(52.819cm^{-1}) = 8339.01cm^{-1}$$
Q13.26
Plot the $$\frac{\nu_{obs}}{\nu}$$ versus $$(\nu +1)$$ for the anharmonic oscillator approximation and use it to determine the values of $$\nu_{e}$$ and $$x_{e}\nu_{e}$$ for $$H^35Cl$$. Use the information in Table13.4.
S13.26
$${\nu}_{obs} = \nu_{obs}\nu - x_{e}\nu_{e}\nu(\nu+1)$$
$$\frac{\nu_{obs}}{\nu} = \nu_{e} - {x}_{e}\nu_{e}(\nu+1)$$
The slope is $$ -x_{e}\nu_{e}$$ and the intercept is $$\nu_{e}$$
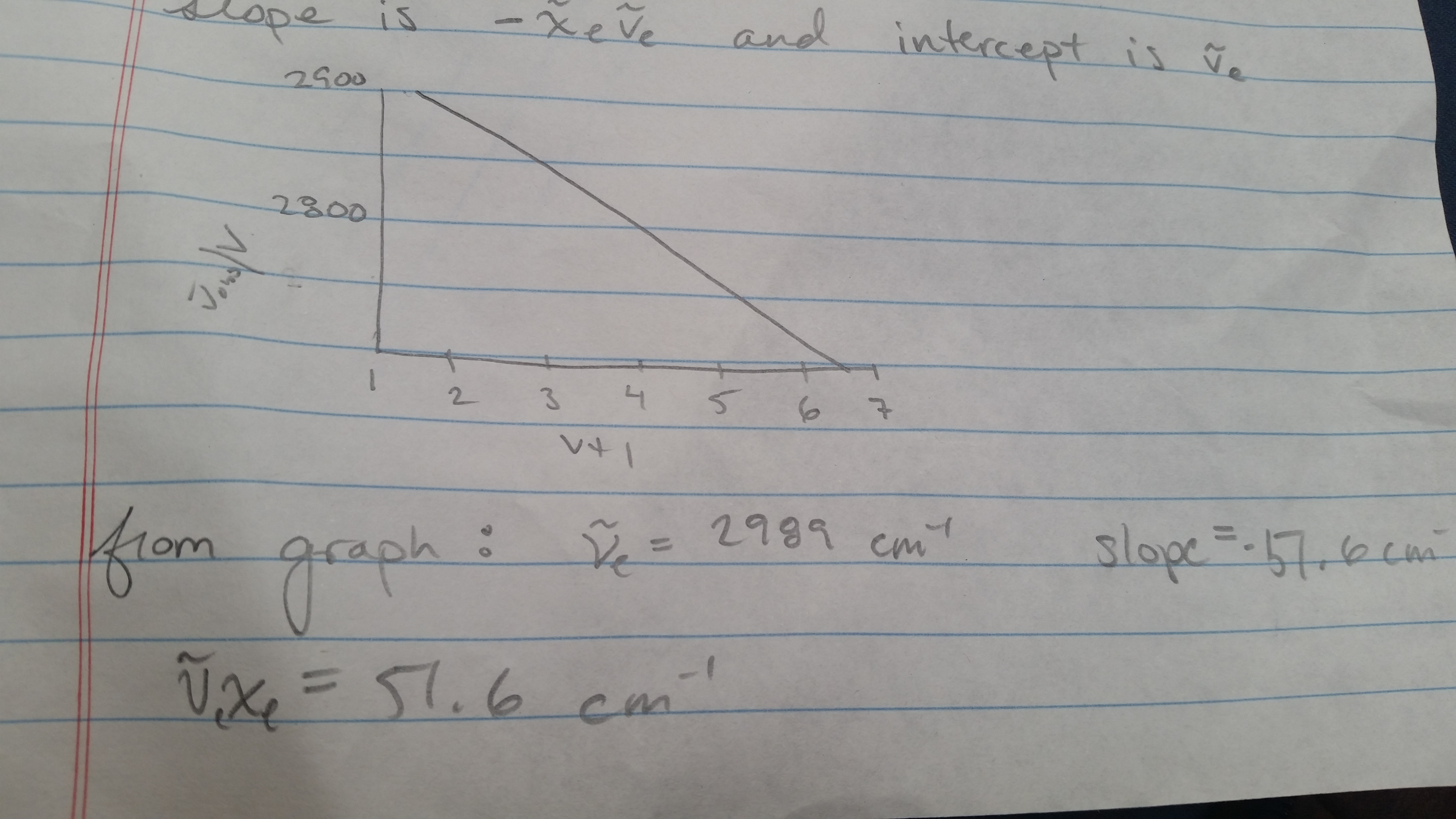
The problem is nice and straight forward. It would be great for an explanation of why the slope is negative for an insight of the graph
Q13.31
Phosphorus nitride (\(PN\)) is a heteronuclear diatomic molecule that is a similar to \(N_2\) with a triple bond, although is substantially weaker because \(P\) is a larger atomic radius than \(N\). Using the following data, calculate \(\tilde{\nu_{e}}'\) and \(\tilde{\chi_{e}}'\) \(\tilde{\nu_{e}}'\) for \(PN\).
| IR Transition | \(\tilde{\nu_{abs}}\) [\(cm^{-1}\)] |
|---|---|
| \( 0 \rightarrow 0 \) | 39,699.10 |
| \( 0 \rightarrow 1 \) | 40,786.80 |
| \( 0 \rightarrow 2 \) | 41,858.90 |
S13.31
We will use the following equation:
\[\tilde{\nu_{abs}} = \tilde{\nu_{0,0}}' + \tilde{\nu_{e}}' \tilde{\nu}' - \tilde{\chi_{e}}' \tilde{\nu_{e}}' \tilde{\nu}' (\nu' + 1) \]
Plugging in the appropriate values of \(\nu' \), we get:
According to your table \( \tilde{\nu_{0,0}}' \) should be 39,699.10 not 29,699.10.
- \(\nu' = 0 \): \[ \tilde{\nu_{0,0}}' = 29,699.10 \; cm^{-1} \tag{1}\]
- \(\nu' = 1 \): \[ \tilde{\nu_{0,0}}' + \tilde{\nu_{e}}' - 2 \tilde{\chi_{e}}' \tilde{\nu_{e}}' = 40,786.80 \; cm^{-1} \tag{2}\]
- \(\nu' = 2 \): \[ \tilde{\nu_{0,0}}' + 2 \tilde{\nu_{e}}' - 6 \tilde{\chi_{e}}' \tilde{\nu_{e}}' = 41,858.90\; cm^{-1} \tag{3}\]
Solving as a system of equations, we subtract:
(2) - (1) = (4), (3) - (1) = (5), and finally (5) - 2x(4) = (6)
Equation (6) can be solved for \(\tilde{\chi_{e}}' \tilde{\nu_{e}}' \), and then plugged back in to equation (4) or equation (5) to solve for \( \tilde{\nu_{e}}' \). The answer is:
\[\tilde{\chi_{e}}' \tilde{\nu_{e}}' = 1103.3\; cm^{-1} \]
and
\[ \tilde{\nu_{e}}' = 7.80 \; cm^{-1} \]
from my calculations \(\tilde{\nu_{e}}' = 1103.3 \) and \( \tilde{\chi_{e}}' \tilde{\nu_{e}}' = 7.80 \) it looks like you had them switched
Q13.32
The frequencies of the first few vibronic transitions to an excited state of NaCl* are as follows:
| Vibronic Transitions | 0 \(\rightarrow\) 0 | 0 \(\rightarrow\) 1 | 0 \(\rightarrow\) 2 |
|---|---|---|---|
| \(\tilde{v}_{obs}/cm^-1\) | 12376 | 89706 | 15219 |
*not accurate values for NaCl
Use these data to calculate the values of \(\tilde{v}_e\) and \(\tilde{v}_e\tilde{x}_e\) for the excited state of NaCl
S13.32
\(A = \tilde{v}_e', B = \tilde{v}_e'\tilde{x}_e'\)
\(12376 = \tilde{v}_0,0\)
\(89706 = \tilde{v}_0,0+\tilde{v}_e'-2\tilde{v}_e'\tilde{x}_e' - 12376 = \tilde{v}_0,0 = 77330 = +\tilde{v}_e'-2\tilde{v}_e'\tilde{x}_e'\) (1)
\(15219 = \tilde{v}_0,0+2\tilde{v}_e'-6\tilde{v}_e'\tilde{x}_e' - 12376 = \tilde{v}_0,0 = 2843 = 2\tilde{v}_e'-6\tilde{v}_e'\tilde{x}_e'\) (2)
77330 + 2B = A (1a)
2843 = 2A - 6B (2a)
77330+2B = A
2843 - 154660 = -2B
B = 75908.5 cm-1 = \(\tilde{v}_e'\)
A = 229147 cm-1 = \(\tilde{v}_e'\tilde{x}_e'\)
Q13.33
Determine the number of translational, rotational, and vibrational degrees of freedom in
- Xe
- HCl
- CS2
- hemoglobin containing 9272 molecules
The total number of degrees of freedom is 3N, where N is the number of atoms in the molecule. All molecules have three translational degrees of freedom. A nonlinear molecule has three rotational degrees of freedom and a linear molecule has two rotational degrees of freedom. A linear molecule has \(3N-5\) vibrational degrees of freedom and a nonlinear molecule has 3N — 6 vibrational degrees of freedom.
S13.33
The number of translational degrees of freedom is 3, the number of rotational degrees of freedom is 2 for linear molecules and 3 for non-linear molecules. Therefore, the remaining degrees of freedom, which is equal to 3N-5 for linear molecules or 3N-6 for non-linear molecules, is equal to the number of vibrational degrees of freedom.
| Translation | Rotation | Vibration | Total | |
|---|---|---|---|---|
| Xe | 3 | 0 | 0 | 3 |
| HCl | 3 | 2 | 1 | 6 |
| CS2 | 3 | 2 | 4 | 9 |
| hemoglobin | 3 | 3 | 27810 | 27816 |
Q13.36
Classify each of the following molecules as either a prolate or an oblate symmetric top: \(XeF_4\), \(ClCH_3\), \(NH_3\), and \(C_6\)\(H_6\).
S13.36
- \(XeF_4\) :oblate
- \(ClCH_3\):prolate
- \(NH_3\):prolate
- \(C_6\)\(H_6\):oblate
Q13.37
Solve for the components of the moment of inertia of a trigonal planar molecule if all the masses are m, the bond lengths are unit length, and all bond angles are \(120^\circ \).
S13.37
\[I_{xx} = \sum m_jy^2_j = m(1)^2 + 2m (sin^2 30^\circ) = \frac{3}{2}m \]
\[I_{yy} = \sum m_jx^2_j = m(0)^2 + 2m (cos^2 30^\circ) = \frac{3}{2}m \]
\[I_{zz} = \sum m_jx^2_j + \sum m_jy^2_j = 3m \]
Q13.38
This problem illustrates how the principal moments of inertia can be obtained as an eigenvalue problem. Consider a molecule where all the masses are unit masses and the long and short bond lengths are 2 and 1, respectively.
Show that
\[ I_{xx} = 2\cos^2\theta + 8\sin^2\theta \]\[ I_{yy} = 8\cos^2\theta + 2\sin^2\theta \]\[ I_{xy} = -6\cos\theta\sin\theta \]
Solve the secular determinant equation for \(\lambda\)
\[\left. \begin{vmatrix} I_{xx} - \lambda & I_{xy} \\ I_{xy} & I_{yy} - \lambda \end{vmatrix} \right. = 0 \]
and compare the result with the values of \(I_{xx}\) and \(I_{yy}\) that you would obtain if you align the "molecule" and coordinate system such that \(\theta = 180^{\circ}\). What does this comparison tell you? What are the values of \(I_{xx}\) and \(I_{yy}\) if \(\theta = 90\)?
S13.38
We use trigonometric functions to find the x and y components
\[I_{xx} = \sum m_{i}y^2_{i} = 2(1)(2\sin\theta)^2 + 2(1)\left[\sin\left(\dfrac{\pi}{2}\right) - \theta\right]^2 = 8\sin^2\theta + 2\cos^2\theta\]
\[I_{yy} = \sum m_{i}x^2_{i} = 2(1)(2\cos\theta)^2 + 2(1)\left[\cos\left(\dfrac{\pi}{2}\right) - \theta\right]^2 = 8\cos^2\theta + 2\sin^2\theta \]
\[I_{xy} = -\sum m_{i}x_{i}y_{i} = -(2\cos\theta)(2\sin\theta) - 2\left[\cos\left(\pi\right) + \theta\right]\left[\sin\left(\pi\right) + \theta\right] - \left[\sin\left(\dfrac{\pi}{2}\right) - \theta\right]\left[\cos\left(\dfrac{\pi}{2}\right) - \theta\right] - \left[\cos\left(\dfrac{\pi}{2}\right) + \theta\right]\left[\sin\left(\dfrac{\pi}{2}\right) + \theta\right] \]
= \( -6\cos\theta\sin\theta\)
The secular determinantal equation becomes
\[\left. \begin{vmatrix} 8\sin^2\theta + 2\cos^2\theta - \lambda & -6\cos\theta\sin\theta \\ -6\cos\theta\sin\theta & 8\cos^2\theta + 2\sin^2\theta - \lambda \end{vmatrix} \right. = 0 \]
Expanding the determinant gives
\[ 0 = \lambda^2 - \lambda(10)(\sin\theta^2 + \cos\theta^2) + 16(\sin\theta^2 + \cos\theta^2)^2 \]
\[0 = \lambda^2 - 10\lambda + 16\]
\[\lambda = 5 \pm 3 \]
If \(\theta = 180^\circ\) then \(I_{xx} = 2, I_{yy} = 8, and I_{xy} = 0\). If \(\theta = 90^\circ\) then \(I_{xx} = 8, I_{yy} = 2, and I_{xy} = 0\). This tells us that the coordinate system does not affect the values of the principal momentum of inertia.
Q13.39
Sketch the energy level diagram of NH3 ( a prolate symmetric top molecule ) and XeF4 ( an oblate symmetric top ). How do they differ?
S13.39
The energies increase as the J levels increases for the prolate symmetry and the energies decrease as J increases for the oblate symmetry

