0: Introduction to Complex Numbers
- Page ID
- 93459
Name: ______________________________
Section: _____________________________
Student ID#:__________________________
Complex Numbers
A complex number is a number that can be expressed in the form \(a + bi\), where \(a\) and \(b\) are real numbers, and \(i\) is the imaginary unit (which satisfies the equation \(i^2 = −1\)). In this expression, \(a\) is called the real part of the complex number, and \(b\) is called the imaginary part. If \({\displaystyle z=a+bi}\), then we write \({\displaystyle \operatorname {Re} (z)=a,}\) and \({\displaystyle \operatorname {Im} (z)=b}\).
Q1
Use the quadratic formula to find roots for \(z^2-2z+5=0\). (Recall that the roots for a quadratic equation, \(ax^2+bx+c=0\), can be found from quadratic formula:
\[x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}.\]
For the quadratic equation, \(z^2-2z+5=0\):
- What is \(z\)?
- What are \({Re} (z)\) and \({Im} (z)\)?
Complex Conjugates
The complex conjugate of a complex number is the number with equal real part and imaginary part equal in magnitude, but the complex value is opposite in sign. For example, the complex conjugate of \(3 + 4i\) is \(3 − 4i\). In general, the complex conjugate of a complex number is simply that number with the sign of the imaginary part reversed, that is, if \(z=x+iy\), then the complex conjugate is \(z^*=x-iy\).
Q2
What is the value of \(xy^*\) for the following complex numbers:
- \(x= 3 + 5i\) and \(y = 2 - 3i\)
- \(x= 5 + 1i\) and \(y = 3 + i\)
- \(x = y = 5 + 5i\)
- \(x = y = -3 + 2i\)
Q3
Which sums in Q2 are real? Can you identify the pattern for when the sum of two complex numbers will be real?
Plotting Complex Numbers
Complex numbers extend the concept of the one-dimensional number line to the two-dimensional complex plane by using the horizontal axis for the real part and the vertical axis for the imaginary part. The complex number \(a + bi\) can be identified with the point \((a, b)\) in the complex plane. A complex number whose real part is zero is said to be purely imaginary, whereas a complex number whose imaginary part is zero is a real number. In this way, the complex numbers are a field extension of the ordinary real numbers, in order to solve problems that cannot be solved with real numbers alone. We often conceptualize complex numbers in a graphical manner, on a complex plane. The real part is the \(x\)-axis, and the imaginary part is the \(y\)-axis.
Q4
What is the length of the vector shown in the figure? This can be computed using the Pythagorean theorem.

Absolute Value
The absolute value or modulus \(|x|\) of a real number \(x\) is the non-negative value of \(x\) without regard to its sign (i.e., \(|x| = x\) for a positive \(x\), \(|x| = −x\) for a negative \(x\) when \(-x\) is positive, and \(|0| = 0\)). the definition given above for the real absolute value cannot be directly generalized for a complex number. However the geometric interpretation of the absolute value of a real number as its distance from 0 can be generalized. The absolute value of a complex number is defined as its distance in the complex plane from the origin. That product of any complex number \(z\) and its complex conjugate \(z^*\) is always a non-negative real number.
Q5
When is \(z^*z = z^2\)?
Phase Angle
We refer to the angle, \(\theta\), shown in the figure above, as the phase angle. We can find it from the legs of the triangle, that is \(\theta =\tan{\frac{y}{x}}\).

Q6
For \(z=2+2i\), what is the length of this vector and what is its phase angle?
Euler's Formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that, for any real number x:
\[ e^{i\theta}=\cos{\theta}+i\sin{\theta}\]
This is
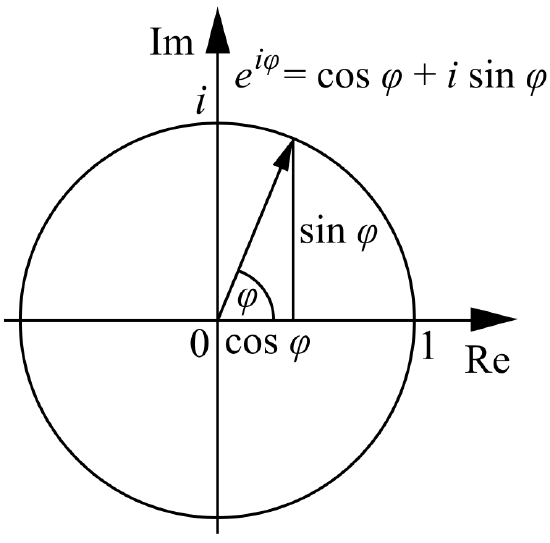
From this. Then \(x=r\cos{\theta}\) and \(y=r\sin{\theta}\).
Q7
The property involving the product of exponentials
\[ e^{a}e^{b}=e^{a+b}\]
also applies to complex arguments.
What is the product of \(e^{4+3i}\) and \(e^{5+2i}\)?
Q8
What is the product of \(e^{z}\) and \(e^{z^*}\) where \(z\) is any complex number?
Relationship to Trigonometry
Euler's formula provides a powerful connection between analysis and trigonometry, and provides an interpretation of the sine and cosine functions as weighted sums of the exponential function:
\[{\begin{align}\cos x&=\operatorname {Re} \left(e^{ix}\right)={\frac {e^{ix}+e^{-ix}}{2}}\\\sin x&=\operatorname {Im} \left(e^{ix}\right)={\frac {e^{ix}-e^{-ix}}{2i}}\end{align}}\]
Q9
Expand \(y= \cos x \sin x\) into a function of complex exponentials


