9.E: The Chemical Bond- Diatomic Molecules (Exercises)
- Page ID
- 92429
Solutions to select questions can be found online.
9.3
The overlap integral and other integrals that arise in two-center systems like that of H2 which is called a two-center integral. The two center integrals are much easier being evaluated by simply using the coordinate system, elliptic coordinates. In the coordinate system, where there are simply two fixed points which are separated by distance \(R\).
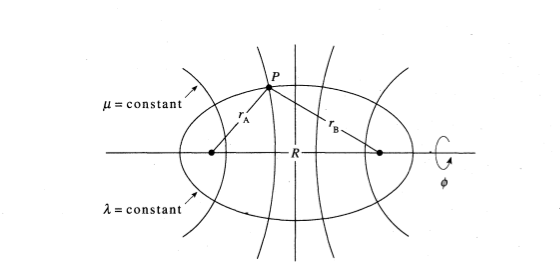
A point \(P\) is given by three coordinates which are
- \(λ= r_A + r_B / R\)
- \(µ= r_A + r_B / R\)
the angle ø is the angle that (\(r_A\), \(r_B\), \(R\)) triangle makes the interfocal axis. The differential volume element (elliptic coordinates) ⇔ \(dr= R^3/ 8 (λ^2 - \mu^2) dλ\,dµ\,dø\)
Given definitions \(λ\), \(\mu\), \(\phi\) → prove that
- \(1≤ λ < ∞\)
- \(-1≤ µ ≤ 1\)
- \(0 ≤ \phi ≤ 2π\)
Use elliptic coordinates to evaluate the overlap integral.
Use Equation:
\[S= \int dr \,1s_A1s_B = \dfrac{Z^3}{π} \int dr \,e^{-Zr_A} e^{-Zr_B} \nonumber\]
- Solution
-
From simple inspection of the figure:
- Have \(r_A + r_B\) is never less than that of \(R\). Therefore, \(1≤ λ < ∞\).
- \(r_A - r_B\) can never have a of magnitude greater that that of \(R\), therefore have \(-1≤ \mu ≤ 1\).
- The variable \(\phi\) can undergo 1 complete revolution therefore have/get \(0 ≤ \phi ≤ 2π\).
Knowing all of this information, we can now solve for this equation:
\[\begin{align*} S &= \dfrac{Z^3}{π} \int dr e^{-ZrA} e^{-Zr)B} \\[4pt] &= \dfrac{Z^3}{π} ∫_0^{2\pi} d\phi \int_1^{∞} dλ \int _{-1}^{1} d\mu R^3/8 (λ^2 - µ^2) e^{-Z(r_A + r_B)} \\[4pt] &= \dfrac{R^3Z^3}{4} ∫_1^∞ dλ \int_{-1}^{1} d\mu (λ^2 - \mu^2) e^{-ZR λ} \\[4pt] &= \dfrac{R^3Z^3}{4} ∫_1^∞ d λ e^{-ZR λ} ∫_{-1}^1 dµ (λ^2 - µ^2) \\[4pt] &= \dfrac{R^3Z^3}{4} ∫^∞_{1} dλ e^{-ZRλ} (2λ^2 - 2/3) \\[4pt] &= \dfrac{R^3Z^3}{2} \left[(1/ZR + 2/Z^2R^2 + 2/Z^3R^3) e^{-ZR} - 1/3ZR e^{-ZR}\right] \\[4pt] &= e^{-ZR}(1+ZR + Z^2R^2/3) \end{align*}\]
9.4
Repeat the calculation in 9.3 for \({\psi}_-={1s_A-1s_B}\)
- Solution
-
\[E_-=\dfrac{\int{dr{\psi}^*_-H{\psi}_-}}{\int{dr{\psi}^*_-{\psi}_-}}\nonumber \]
The denominator is
\[\int{dr{\psi}^*_-{\psi}_-}=2(1-S)\nonumber \]
The numerator can be evaluated using equations 9.18, 9.19, 9.20, 9.21 with a simple exchange of a minus sign in equations 9.18 and 9.21,
\[\int{dr{\psi}^*_-H{\psi}_-}=2E_{1s}\left(1+S\right)+2J-2K\nonumber \]
So
\[E_-=\dfrac{2E_{1s}\left(1+S\right)+2J-2K}{2(1-S)}\nonumber \]
9.9
Show that the \(2p_x\) and the \(2p_y\) orbitals do not overlap. Use \(2p_x \equiv C\cos\theta\) and \(2p_y \equiv C\sin\theta \cos\theta \) and \(f(r)\) as the radial component.
- Solution
-
If \(\int \Psi_1 \Psi_2 dr \neq 0\) then the orbitals overlap.
Substituting in:
\[\int C\cos^2\theta \sin\theta f(r) \nonumber \]
\[C\int_0^\pi cos^2\theta \sin\theta \int_0^\infty f(r)\neq 0 \nonumber \]
This orbitals do not overlap.
9.10
what does the overlap integral represent?
- Solution
-
The overlap integral represents the amount of overlap there is between the orbitals of 2 or more different nuclei. It is only significant for orbitals that have a large overlap. It is a component of the energy integral of the nuclei.
9.14
Which of the three species is the is the least stable due to bond order: \(\ce{O2}\), \(\ce{O2^{+}}\), \(\ce{O_2^{2-}}\). Hint it may be helpful to draw molecular orbitals for each species although it is not required.
- Solution
-
We have to use the bond order formula for each of the situations.
Bond order = \( \dfrac{(\text{number of bonding electrons})- (\text{number of anti-bonding electrons})}{2} \)
For O2: We have 12 valence electrons. ThereforeBond order = \( \dfrac{10 - 8}{2} = 1 \)
From the bond orders, we can see that O22- is the least stable.
Bond order = \(\dfrac{10 - 5}{2}= \dfrac{5}{2}\)
For O22-: We have 14 valence electrons. ThereforeBond order =\( \dfrac{10 - 6}{2} = 2\)
For O2+: We have 11 valence electrons. Therefore
9.17
Write the electron configuration and bond order of carbon monoxide.
- Solution
-
The electron configuration for carbon monoxide
\[ CO: KK(\sigma_{2s})^2(\sigma^*_{2s})^2(\pi_{2p})^4(\sigma2_{p_z})^2\nonumber \]
The bond order of \(\ce{CO}\) is three.
9.17
Determine the bond order diphosphorus \(\ce{P2}\).
- Solution
-
Each phosphorus atom will contribute 5 valence electrons, so there will be a total of 10 valence electrons. We use these ten valence electrons to fill up atomic orbitals and we learn that the ground state electron configuration has 8 electron in bonding orbitals and 2 electrons in antibonding orbitals. To find bond order we take bonding electrons(8 electrons) minus antibonding (2 electrons) and divide by 2 to find the bond order of 3.
9.18
Determine the bond order for the bond in nitrogen oxide cation, \(\ce{NO^{+}}\).
- Solution
-
The equation for bond order is
\[\text{Bond Order} = \dfrac{1}{2}[(\text{# of electrons in bonding orbitals}) - (\text{# of electron in antibonding orbitals})]\nonumber \]
There are 10 electrons total in the \(2p\) level that have to fill the \(\sigma_1, \sigma^{*}_1, \pi, \sigma_2, \pi^{*} \sigma^{*}_2\) in order of increasing energy, respectively. If one fills out the MO diagram, they will find that the number of bonding electrons is \( 8\) and the number of antibonding electrons is \(2\).
Thus, the bond order is
\[\dfrac{1}{2} [8 - 2] = 3\nonumber \]
This indicates that there is triple bond for \(NO^{+}\)
9.18
What is the electron configuration and bond order of nitric oxide ion?
- Solution
-
The electron configuration of \(NO^+\) is
\[NO^+: KK(\sigma2s)^2(\sigma^*2s)^2(\pi 2p)^4(\sigma2p_z)^2(\pi^*2p)^1\nonumber \]
The bond order of \(NO^+\) is \(2\dfrac{1}{2}\)
9.21
Determine the bond order for the \(NO\) molecule.
- Solution
-
Bond Order = [(# of binding electrons) - (# of anitbonding electrons)] /2
From drawing the Molecular Orbital Diagram, we find that there are 6 binding electrons and 1 antibonding electron, therefore,
Bond Order = (6-1)/2 =5/2
9.22
How is the energy-level diagram for diatomic OH radical differ from that of NH? What is the highest occupied molecular orbital of OH?
9.23
If a light source generates a light at 73.4 nm while a photoelectron spectrometer is measuring the kinetic energy of the electrons ionized when the molecule absorbs this light, what is the largest electron binding energy that can be measured? Also, is it possible to determine the energy of the occupied molecular orbitals of a molecule using the kinetic energy of the ionized electrons measured? If yes, explain. Hint : Recall the photoelectron effect discussed in lecture 2.
- Solution
-
The energy of the source light is
\[E = \dfrac{hc}{\lambda} = 2.71 \times 10^{-18} \;J\nonumber \]
So 2.71 x 10-18 J is the largest electron binding energy that can be measured using this radiation source.
Using Einstein's explanation of the photoelectric effect, we know that
\[\varphi + KE = h\nu\nonumber \]
Hence, if we know the kinetic energy of the ionized electrons, as well as the energy absorbed by the electron v, we can find φ, which is the energy of the molecular orbital occupied by the electron being ionized.
9.24
Why would the ionization energy of a \(3p\) electron from HCl molecule be lower than a \(3p\) electron from a chlorine atom?
- Solution
-
The electrons that are shared between the two atoms in HCl are pulled closer to the Chlorine atom because it has a greater electronegativity than hydrogen. This creates a dipole moment and the bonding electrons become localized in such a way that they shield the nonbonding \(3p\) electrons on the chlorine atom more than the inner shells of just a chlorine atom. Since shielding is greater for HCl the electrons require less energy to be pulled away from the molecule. Less shielded valence electrons will experience a greater attractive force decreasing the radius and increasing ionization energy.
9.27
Photoelectron spectroscopy involves the measurement of kinetic energy of photoelectrons to determine the binding energy, intensity and angular distributions of these electrons and use the information obtained to examine the electronic structure of molecules. It differs from the conventional methods of spectroscopy in that it detects electrons rather than photons to study electronic structures of a material. The \(O_2\) photoelectron spectrum emits two bands of 52.3898 MJ* mol^{-1} and 52.311 MJ*mol^{-1}. This emission corresponds to the 1\(\s) ionization of the oxygen electron. In your own words explain the observation.
- Solution
-
The two bands that oxygen is emitted corresponds to the spin \((+ \dfrac{1}{2}, - \dfrac{1}{2})\) ionization in the 1\(s\) electron. The marginal difference in energy is due to the spin-orbit coupling, which is also known as spin-pairing. Spin-orbit coupling describes the weak magnetic interaction between the orbital motion and the particle spin in a particle
9.28
Would the ionization energies of non-bonding 1s electrons be different for HCl and Cl2?
- Solution
-
The shielding effects for the 1s electrons are different for these two systems. In HCl, the bonding electron is localized on the more electronegative Cl, while in Cl2 the bonding electrons are right in between the two atoms. This means that the 1s electrons are more shielded in HCl than in Cl2 , and so the electron is easier to rip off in HCl. So the ionization energy for 1s electrons in HCl is smaller than in Cl2.
9.28
First write out the ground-state electron configuration for the homonuclear diatomic molecule \(F_2\). Then given the experimental ionization energies for a 1s fluorine electron for HF and \(F_2\) as 66.981 and 67.217 \(MJ \centerdot mol^{-1}\), explain why even though the 1s electrons of fluorine are not involved in the chemical bonds their ionization energies are different.
- Solution
-
The ground state configuration is
\[(1\sigma_g)^2(1\sigma_u)^2(2\sigma_g)^2(2\sigma_u)^2(3\sigma_g)^2(1\pi_u)^2(1\pi_u)^2(1\pi_g)^2(1\pi_g)^2\nonumber \]
The ionization energies are different because the 1s electrons affect the attraction of those electrons to the nucleus, even though they are not involved in the actual bond. The \(F_2\) bonding electrons are equally distributed between two atoms, whereas the HF bonding electrons are localized on the fluorine atom. Therefore there is increased shielding of the 1s orbital on HF which causes a smaller ionization energy.
9.30
Try to solve for the ground-state term symbols for the diatomic molecules H2+ and H2, given that the ground-state electron configuration for H2+ is \((\sigma_g1s)^1\) and for H2 is \((\sigma_g1s)^2\).
- Solution
-
(1σg)1 corresponds to ML=0 and Ms=1/2, meaning that there is an unpaired electron in the symmetric molecular orbitals of g and there is change in the 1σg wavefunction. The ground-state term symbol for H2+ will then be \[^2\Sigma^+_g\]
(1σg)2 corresponds to ML=0 and Ms=0, meaning that there is an unpaired electron in the molecular orbitals of g and there is change in the 1σg wavefunction. The ground-state term symbol for H2 will then be \[^1\Sigma^+_g\]
9.30
Find the ground-state term symbols for \(B_{2}\).
- Solution
-
The ground state electron configuration is
\[(1\sigma_{g})^{2} (1\sigma_{u})^{2} (2\sigma_{g})^2 (1\pi_{u})^1 (1\pi _{u})^1\nonumber \]
We do not care about the filled orbitals because their
\[M_{L}=M_{S} =0\nonumber \]
The two unfilled orbitals are
\[(1\pi_{u})^1 (1\pi_{u})^1\nonumber \]
all possible combinations of
\[m_{l1}, m_{s1}, m_{l2}, m_{s2} \nonumber \]
for \(B_{2}\) are:
\[M_{S}, M_{L}: \nonumber \]
\[(0, 2): 1^+, 1^-\nonumber \]
\[(0,0): 1^-, -1^+\nonumber \]
\[(0, -2): -1^+, -1^-\nonumber \]
With these possible combinations we find the following to be possible ground state term symbols:
\[^1\Delta, ^3\Sigma, ^1\Sigma\nonumber \]
Following Hund's Rule we detect \(^3\Sigma\) to be our ground-state term symbol because the largest spin multiplicity will be the ground state of \(B_2\). Now we take the two unoccupied orbitals and take the product to get the symmetry of the molecular orbital.
\[u \cdot u = g\nonumber \]
So the ground-state term symbol for \[B_2\nonumber \] is: \(^3 \Sigma_{g}^-\)
9.31
Solve for the ground-state molecular term symbols for O2, N2, N2+, and O2+.
- Solution
-
The ground state molecular term symbols are given below:
O2
The molecular term symbol of O2 without the ± designation is 3\(\Sigma\)g. The electron configuration is (filled orbital) (1\(\pi\)g2\(p\)x)1(1\(\pi\)g2\(p\)y)1, so the symmetry with respect to a reflection through the \(x\)-\(z\) plane is (+) (-) = (-); therefore, the complete molecular term symbol of O2 is 3\(\Sigma\)g-.
N2
(1\(\sigma\)g)2 (1\(\sigma\)u)2 (2\(\sigma\)g)2(2\(\sigma\)u)2(1\(\pi\)u)2(1\(\pi\)u)2(3\(\sigma\)g)2 Corresponds to | \(M\)\(L\) | = 0 and | \(M\)\(S\) | = 0 of a 1\(\Sigma\) term symbol. The symmetry of the molecule is \(g\). The complete ground state term symbol of N2 is 1\(\Sigma\)g+ because the molecular wave function does not change when reflected through a plane containing the two nuclei.
N2+
(1\(\sigma\)g)2 (1\(\sigma\)u)2 (2\(\sigma\)g)2(2\(\sigma\)u)2(1\(\pi\)u)2(1\(\pi\)u)2(3\(\sigma\)g)1 Corresponds to | \(M\)\(L\) | = 0 and | \(M\)\(S\) | = 0.5 of a 2\(\Sigma\) term symbol. The symmetry of the molecule is \(g\). The complete ground state term symbol of N2+ is 2\(\Sigma\)g+ because the molecular wave function does not change when reflected through a plane containing the two nuclei.
O2+
(1\(\sigma\)g)2 (1\(\sigma\)u)2 (2\(\sigma\)g)2(2\(\sigma\)u)2(3\(\sigma\)g)2(1\(\pi\)u)2(1\(\pi\)u)2(1\(\pi\)g)1 Corresponds to | \(M\)\(L\) | = 1 and | \(M\)\(S\) | = 0.5 of a 2\(\Pi\) term symbol. The symmetry of the molecule is \(g\), since the only unfilled molecular orbital has symmetry \(g\), so the complete ground state term symbol of O2+ is 2\(\Pi\)\(g\).

