8.5: Wavefunctions must be Antisymmetric to Interchange of any Two Electrons
- Last updated
- Save as PDF
- Page ID
- 92404
Learning Objectives
- Interprete the consequence of exchanging two electrons in a multi-electron atom on the wavelengths
- Connect the Pauli’s Exclusion Principle to the permutation symmetry of multi-electron atoms
Quantum mechanics allows us to predict the results of experiments. If we conduct an experiment with indistinguishable particles a correct quantum description cannot allow anything which distinguishes between them. For example, if the wavefunctions of two particles overlap, and we detect a particle, which one is it? The answer to this is not only that we do not know, but that we cannot know. Quantum mechanics can only tell us the probability of finding a particle in a given region. The wavefunction must therefore describe both particles.
The Schrödinger equation for the helium atom is then:
\[ \left[ - \dfrac{\hbar^2}{2m} ( \nabla^2_1 + \nabla^2_1 ) - V(\mathbf{r}_1) - V(\mathbf{r}_2) + V_{12}(\mathbf{r}_1,\mathbf{r}_2) \right ] \psi(\mathbf{r}_1, \mathbf{r}_2) = E\psi(\mathbf{r}_1, \mathbf{r}_2) \nonumber \]
where the subscripts label each particle, and there are six coordinates, three for each particle. While \(|\psi(\mathbf{r}_1, \mathbf{r}_2) \rangle \) is a six dimensional wavefunction (three for each electron) and contains all the information we can measure (a Postulate of Quantum Mechanics), it only provide the probability of finding the electron at a specific volume element, and does not tell us which particle is which (e.g., is it electon \(1\) or electron \(2\)?).
What basis states would be appropriate for \(|\psi \rangle\)? If we consider the orbital approximation that uses a product wavefunction
\[|\psi(\mathbf{r}_1, \mathbf{r}_2) \rangle = |\varphi_a (\mathbf{r}_1) \rangle | \varphi_ b(\mathbf{r}_2)\rangle \nonumber \]
where \( | \varphi_a(\mathbf{r}_1)\rangle\) and \( | \varphi_b(\mathbf{r}_2)\rangle\) are one-particle spin-orbitals (with both spin and spatial components) of atoms 1 and 2. This approximation allows us to separate the two particle equation into two one-electron equations:
\[ \left[ - \dfrac{\hbar^2}{2m} \nabla^2_1 + V(\mathbf{r}_1) \right ] |\varphi_a(\mathbf{r}_1) \rangle = E|\varphi_a(\mathbf{r}_1) \rangle \nonumber \]
\[ \left[ - \dfrac{\hbar^2}{2m} \nabla^2_2 + V(\mathbf{r}_2) \right ] |\varphi_b(\mathbf{r}_2) \rangle= E|\varphi_a(\mathbf{r}_2) \rangle \nonumber \]
provided that the particles do not interact (e.g., \(\nabla^2_1 \) does not act on \(|\varphi_b(\mathbf{r}_2)\rangle\) and \(V_{12} = 0\)).
Unfortunately, by doing this we have introduced unphysical labels to the indistinguishable particles. And this is wrong: the effect of it is that the particles do not interfere with each other because they are in different dimensions (six dimensional space - remember?). When we construct a two particle wavefunction out of two one-particle wavefunctions we must be ensure that the probability density (the measurable quantity \(|\psi|^2\)) is independent of the artificial labels.
The Exchange Operator
We can deepen our understanding of the quantum mechanical description of multi-electron atoms by examining the concepts of electron indistinguishability and the Pauli Exclusion Principle in detail. We will use the following statement as a guide to keep our explorations focused on the development of a clear picture of the multi-electron atom: “When a multi-electron wavefunction is built as a product of single-electron wavefunctions, the corresponding concept is that exactly one electron’s worth of charge density is described by each atomic spin-orbital.”
A subtle, but important part of the conceptual picture, is that the electrons in a multi-electron system are not distinguishable from one another by any experimental means. Since the electrons are indistinguishable, the probability density we calculate by squaring the modulus of our multi-electron wavefunction also cannot change when the electrons are interchanged (permuted) between different orbitals. In general, if we interchange two identical particles, the world does not change. As we will see below, this requirement leads to the idea that the world can be divided into two types of particles based on their behavior with respect to permutation or interchange.
In order for the probability density to remain unchanged when two particles are permuted, the wavefunction itself can change only by a factor of \(e^{i\varphi}\), which represents a complex number, when the particles described by that wavefunction are permuted. As we will show below, the \(e^{i\varphi}\) factor is possible because the probability density depends on the absolute square of the function and all expectation values involve \(\psi \psi ^*\). Consequently \(e^{i\varphi}\) disappears in any calculation that relates to the real world because \(e^{i\varphi} e^{-i\varphi} = 1\).
We could symbolically write an approximate two-particle wavefunction as \(\psi (\mathbf{r}_1, \mathbf{r}_2)\). This could be, for example, a two-electron wavefunction for helium. To exchange the two particles, we simply substitute the coordinates of particle 1 (\(\mathbf{r}_1\)) for the coordinates of particle 2 (\(\mathbf{r}_2\)) and vice versa, to get the new wavefunction \(\psi (\mathbf{r}_1, \mathbf{r}_2)\). This new wavefunction must have the property that
\[|\psi (\mathbf{r}_1, \mathbf{r}_2)|^2 = \psi (\mathbf{r}_2, \mathbf{r}_1)^*\psi (\mathbf{r}_2, \mathbf{r}_1) = \psi (\mathbf{r}_1, \mathbf{r}_2)^* \psi (\mathbf{r}_1, \mathbf{r}_2) \label {8.5.1} \]
since the probability density of the electrons in the atom does not change upon permutation of the electrons.
Exercise 8.5.1
Permute the electrons the product function for He wavefunction:
\[ \psi (\mathbf{r}_1,\mathbf{r}_2) \rangle = | \varphi_{1s}(\mathbf{r}_1) \rangle | \varphi_{1s}(\mathbf{r}_2) \rangle \nonumber \]
Equation \(\ref{8.5.1}\) will be true only if the wavefunctions before and after permutation are related by a factor of \(e^{i\varphi}\),
\[\psi (\mathbf{r}_1, \mathbf{r}_2) = e^{i\varphi} \psi (\mathbf{r}_1, \mathbf{r}_2) \label {8.5.2} \]
so that
\[ \left ( e^{-i\varphi} \psi (\mathbf{r}_1, \mathbf{r}_2) ^*\right ) \left ( e^{i\varphi} \psi (\mathbf{r}_1, \mathbf{r}_2) ^*\right ) = \psi (\mathbf{r}_1 , \mathbf{r}_2 ) ^* \psi (\mathbf{r}_1 , \mathbf{r}_2) \label {8.5.3} \]
If we exchange or permute two identical particles twice, we are (by definition) back to the original situation. If each permutation changes the wavefunction by \(e^{i \varphi}\), the double permutation must change the wavefunction by \(e^{i\varphi} e^{i\varphi}\). Since we then are back to the original state, the effect of the double permutation must equal 1; i.e.,
\[e^{i\varphi} e^{i\varphi} = e^{i 2\varphi} = 1 \label {8.5.4} \]
which is true only if \(\varphi = 0 \) or an integer multiple of \(\pi\). The requirement that a double permutation reproduce the original situation limits the acceptable values for \(e^{i\varphi}\) to either +1 (when \(\varphi = 0\)) or -1 (when \(\varphi = \pi\)). Both possibilities are found in nature.
Exercise 8.5.2
Use Euler’s Equality
\[e^{i\pi} + 1=0 \nonumber \]
to show that \(e^{i 2\varphi} = 1\) when \(\varphi = 0\) or \(n \pi\) and consequently \(e^{i \varphi} = \pm 1\).
We can introduce the exchange operator \(\hat{P}_{12}\): an operator which permutes the labels of the particles in a multi-particle wavefucntion. This is a rather strange operator, because it only changes the unphysical labels which we have attached to the one-particle wavefunctions in order to make the maths more easy. For a meaningful solution we must have a wavefunction which has a probability amplitude unchanged by \(\hat{P}_{12}\): it must be either symmetric or antisymmetric with respect to exchange:
\[\hat{P}_{12} |\psi(\mathbf{r}_1, \mathbf{r}_2) \rangle = \pm |\psi(\mathbf{r}_2, \mathbf{r}_1) \rangle \label{exchange} \]
Bosons and femions
Physical solutions must be eigenfunctions of \(\hat{P}_{12}\) (i.e., \(\hat{H}\) and \(\hat{P_{12}}\) commute). Moveover, Equation \ref{exchange} argues that the eigenvalues of the Exchange Operator are either +1 (bosons) or −1 (fermions).
Bosons
Wavefunctions for which \(e^{i \varphi} = +1\) are defined as symmetric with respect to permutation, because the wavefunction is identical before and after a single permutation. Wavefunctions that are symmetric with respect to interchange of the particles obey the following mathematical relationship,
\[\hat{P}_{12} |\psi(\mathbf{r}_1, \mathbf{r}_2) \rangle = + |\psi(\mathbf{r}_2, \mathbf{r}_1) \rangle \nonumber \]
The behavior of some particles requires that the wavefunction be symmetric with respect to permutation. These particles are called bosons and have integer spin such as deuterium nuclei, photons, and gluons.
Fermions
The behavior of other particles requires that the wavefunction be antisymmetric with respect to permutation \((e^{i\varphi} = -1)\). A wavefunction that is antisymmetric with respect to electron interchange is one whose output changes sign when the electron coordinates are interchanged, as shown below.
\[\hat{P}_{12} |\psi(\mathbf{r}_1, \mathbf{r}_2) \rangle = - |\psi(\mathbf{r}_2, \mathbf{r}_1) \rangle \nonumber \]
These particles are called fermions and have half-integer spin and include electrons, protons, and neutrinos. Since electrons are fermion, any wavefunction used to describe multiple electrons must be antisymmetric with respect to permutation of the electrons. The requirement that the wavefunction be antisymmetric applies to all multi-electron functions \(\psi (\mathbf{r}_1, \mathbf{r}_2, \cdots r_i)\), including those approximated as products of single electron functions
\[| \psi (\mathbf{r}_1, \mathbf{r}_2, \cdots r_i) \rangle \approx \varphi _a (\mathbf{r}_1) \varphi _b (\mathbf{r}_2) \cdots \varphi _i (r_i) \label{Product} \]
Exercise 8.5.4
What is meant by the term permutation symmetry?
Exercise 8.5.5
Explain why the product function \(\varphi (\mathbf{r}_1) \varphi (\mathbf{r}_2)\) could describe two bosons (deuterium nuclei), but can not describe two fermions (e.g. electrons).
- Answer
-
Because if we switch \(\mathbf{r}_1\) and \(\mathbf{r}_2\), the product function becomes \(φ(r_2)φ(r_1)\), which is equal to \(φ(r_1)φ(r_2)\), which is consistent with the wavefunctions of bosons, because boson wavefunctions are symmetric. However, fermion wavefunctions are antisymmetric, which means that if switch r1 and r2, the result should be -1×the original wavefunction. Therefore, the product function \(φ(r_1)φ(r_2)\) cannot describe fermions.
The Pauli’s Exclusion Principle
Any physically meaningful Hamiltonian must commute with \(\hat{P}_{12}\), otherwise \(\hat{H}\) and \(\hat{P}_{12}\) could not have common eigenfunctions and the system could not remain in an eigenstate of exchange. A simple product wavefunction like that in Equation \(\ref{Product}\) does not satisfy this (unless \( \varphi_a = \varphi_b\)). A linear combination of all permutations is required to satisfy indistinguishability constraints.
For a two particle system (e.g., Helium) there is the asymmetric combination
\[|\psi^{−} \rangle = \dfrac{1}{\sqrt{2}} |\varphi_a(\mathbf{r}_1)\varphi_b(\mathbf{r}_2) − \varphi_a(\mathbf{r}_2)\varphi_b(\mathbf{r}_1) \rangle \label{ASym} \]
and symmetric combination
\[ |\psi^{+} \rangle = C_{ab} |\varphi_a(\mathbf{r}_1)\varphi_b(\mathbf{r}_2) + \varphi_a(\mathbf{r}_2)\varphi_b(\mathbf{r}_1) \rangle + C_{aa} |\varphi_a(\mathbf{r}_2)\varphi_a(\mathbf{r}_1) \rangle + C_{bb}|\varphi_b(\mathbf{r}_2)\varphi_b(\mathbf{r}_1) \rangle \label{Sym} \]
where the \(C_{ab}\) terms are expansion and normalization parameters.
Note that the antisymmetric combination (Equation \(\ref{ASym}\)) cannot include terms where both particles are in the same state (spin-orbital), but there are three possibilities for the symmetric state (Equation \(\ref{Sym}\)).
Although any linear combinations of \(C_{ab}\), \(C_{bb}\), and \(C_{aa}\) in Equation \(\ref{Sym}\) is possible, there are three limiting expressions for possible symmetric combinations:
\[ \begin{align} |\psi^{+i}_1 \rangle &= C_{ab} |\varphi_a(\mathbf{r}_1)\varphi_b(\mathbf{r}_2) + \varphi_a(\mathbf{r}_2)\varphi_b(\mathbf{r}_1) \rangle \\[4pt] |\psi^{+i}_2 \rangle &=C_{aa} |\varphi_a(\mathbf{r}_2)\varphi_a(\mathbf{r}_1) \rangle \\[4pt] |\psi^{+i}_3 \rangle &= C_{bb}|\varphi_b(\mathbf{r}_2)\varphi_b(\mathbf{r}_1) \rangle \end{align} \nonumber \]
If \(\varphi_a(\mathbf{r}_1) = \varphi_a(\mathbf{r}_2)\), then \(|\varphi^{−i} \rangle= 0\). Thus there is no possible antisymmetric combination involving electrons in the same state (spin-orbit). This is the Pauli exclusion principle.
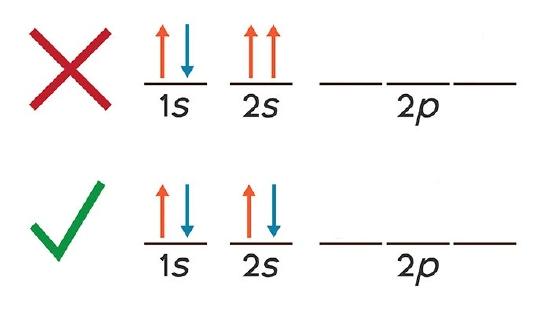
The Pauli Exclusion Principle argues that two electrons could not be described by the same spin-orbital. To see the relationship between this statement and the requirement that the wavefunction be antisymmetric for electrons, try to construct an anti-symmetric wavefunction for two electrons that are described by the same spin-orbital
\[ |\varphi_b(\mathbf{r}_1) \rangle =\varphi_a(\mathbf{r}_2)\rangle \nonumber \]
For example, if this were the case for the anti-symmetric combination for helium (Equation \(\ref{ASym}\)), then the wavefunction collapses to zero. We can only constructs wavefunctions that are antisymmetric with respect to permutation symmetry only if each electron is described by a different function.
The Pauli Exclusion Principle is simply the requirement that the wavefunction be antisymmetric for electrons, since they are fermions.

