1.8: The Bohr Theory of the Hydrogen Atom
- Page ID
- 92343
- Introduce the fundamentals behind the Bohr Atom and demonstrate it can predict the Rydberg's equation for the atomic spectrum of hydrogen
Rutherford's Failed Planetary Atom
Ernest Rutherford had proposed a model of atoms based on the \(\alpha\)-particle scattering experiments of Hans Geiger and Ernest Marsden. In these experiments helium nuclei (\(\alpha\)-particles) were shot at thin gold metal foils. Most of the particles were not scattered; they passed unchanged through the thin metal foil. Some of the few that were scattered were scattered in the backward direction; i.e. they recoiled. This backward scattering requires that the foil contain heavy particles. When an \(\alpha\)-particle hits one of these heavy particles it simply recoils backward, just like a ball thrown at a brick wall. Since most of the \(α\)-particles don’t get scattered, the heavy particles (the nuclei of the atoms) must occupy only a very small region of the total space of the atom. Most of the space must be empty or occupied by very low-mass particles. These low-mass particles are the electrons that surround the nucleus.
There are some basic problems with the Rutherford model. The Coulomb force that exists between oppositely charge particles means that a positive nucleus and negative electrons should attract each other, and the atom should collapse. To prevent the collapse, the electron was postulated to be orbiting the positive nucleus. The Coulomb force (discussed below) is used to change the direction of the velocity, just as a string pulls a ball in a circular orbit around your head or the gravitational force holds the moon in orbit around the Earth. The origin for this hypothesis that suggests this perspective is plausible is the similarity of gravity and Coulombic interactions. The expression for the force of gravity between two masses (Newton's Law of gravity) is
\[F_{gravity} \propto \dfrac{m_1m_2}{r^2}\label{1.8.1} \]
with \(m_1\) and \(m_2\) representing the mass of object 1 and 2, respectively and \(r\) representing the distance between the objects centers
The expression for the Coulomb force between two charged species is
\[F_{Coulomb} \propto \dfrac{Q_1Q_2}{r^2}\label{1.8.2} \]
with \(Q_1\) and \(Q_2\) representing the charge of object 1 and 2, respectively and \(r\) representing the distance between the objects centers.
However, this analogy has a problem too. An electron going around in a circle is constantly being accelerated because its velocity vector is changing. A charged particle that is being accelerated emits radiation. This property is essentially how a radio transmitter works. A power supply drives electrons up and down a wire and thus transmits energy (electromagnetic radiation) that your radio receiver picks up. The radio then plays the music for you that is encoded in the waveform of the radiated energy.
If the orbiting electron is generating radiation, it is losing energy. If an orbiting particle loses energy, the radius of the orbit decreases. To conserve angular momentum, the frequency of the orbiting electron increases. The frequency increases continuously as the electron collapses toward the nucleus. Since the frequency of the rotating electron and the frequency of the radiation that is emitted are the same, both change continuously to produce a continuous spectrum and not the observed discrete lines. Furthermore, if one calculates how long it takes for this collapse to occur, one finds that it takes about \(10^{‑11}\) seconds. This means that nothing in the world based on the structure of atoms could exist for longer than about \(10^{-11}\) seconds. Clearly something is terribly wrong with this classical picture, which means that something was missing at that time from the known laws of physics.
A conservative force is dependent only on the position of the object. If a force is conservative, it is possible to assign a numerical value for the potential at any point. When an object moves from one location to another, the force changes the potential energy of the object by an amount that does not depend on the path taken. The potential can be constructed as simple derivatives for 1-D forces:
\[F = -\dfrac{dV}{dx} \nonumber \]
or as gradients in 3-D forces
\[F = -\nabla V \nonumber \]
where \(\nabla\) is the vector of partial derivatives
\[\nabla = \left ( \dfrac{\partial}{\partial x}, \dfrac{\partial}{\partial y}, \dfrac{\partial}{\partial z} \right) \nonumber \]
The most familiar conservative forces are gravity and Coulombic forces.
The Coulomb force law (Equation \(\ref{1.8.2}\)) comes from the corresponding Coulomb potential (sometimes call electrostatic potential)
\[V(r)=\dfrac{kQ_1 Q_2}{r} \label{1.8.5} \]
and it can be easily verified that the Coulombic force from this interaction (\(F(r)\)) is
\[F(r)=-\dfrac{dV}{dr} \label{1.8.6} \]
As \(r\) is varied, the energy will change, so that we have an example of a potential energy curve \(V(r)\) (Figure \(\PageIndex{2; left}\)). If \(Q_1\) and \(Q_2\) are the same sign, then the curve which is a purely repulsive potential, i.e., the energy increases monotonically as the charges are brought together and decreases monotonically as they are separated. From this, it is easy to see that like charges (charges of the same sign) repel each other.
If the charges are of opposite sign, then the curve appears roughly Figure \(\PageIndex{2; right}\) and this is a purely attractive potential. Thus, the energy decreases as the charges are brought together, implying that opposite charges attract
The Bohr Model
It is observed that line spectra discussed in the previous sections show that hydrogen atoms absorb and emit light at only discrete wavelengths. This observation is connected to the discrete nature of the allowed energies of a quantum mechanical system. Quantum mechanics postulates that, in contrast to classical mechanics, the energy of a system can only take on certain discrete values. This leaves us with the question: How do we determine what these allowed discrete energy values are? After all, it seems that Planck's formula for the allowed energies came out of nowhere.
The model we will describe here, due to Niels Bohr in 1913, is an early attempt to predict the allowed energies for single-electron atoms such as \(\ce{H}\), \(\ce{He^{+}}\), \(\ce{Li^{2+}}\), \(\ce{Be^{3+}}\), etc. Although Bohr's reasoning relies on classical concepts and hence, is not a correct explanation, the reasoning is interesting, and so we examine this model for its historical significance.
Consider a nucleus with charge \(+Ze\) and one electron orbiting the nucleus. In this analysis, we will use another representation of the constant \(k\) in Coulomb's law (Equation \(\ref{1.8.5}\)), which is more commonly represented in the form:
\[k=\dfrac{1}{4\pi \epsilon_0} \label{1.8.7} \]
where \(\epsilon_0\) is known as the permittivity of free space with the numerical value \(\epsilon_0 = 8.8541878\times 10^{-12} \ C^2 J^{-1} m^{-1}\).
The total energy of the electron (the nucleus is assumed to be fixed in space at the origin) is the sum of kinetic and potential energies:
\[E_{total}=\underset{\text{kinetic energy}}{\dfrac{p^2}{2m_e}} - \underset{\text{potential energy}}{\dfrac{Ze^2}{4\pi \epsilon_0 r}} \nonumber \]
The force on the electron is
\[\vec{F}=-\dfrac{Ze^2}{4\pi \epsilon_0 r^3}r \nonumber \]
and its magnitude is
\[F=|\vec{F}|=\dfrac{Ze^2}{4\pi \epsilon_0 r^3}|r|=\dfrac{Ze^2}{4\pi \epsilon_0 r^2} \nonumber \]
since \(\vec{F}=m_e \vec{a}\), the magnitude, it follows that \(|\vec{F}|=m_e |\vec{a}|\). If we assume that the orbit is circular, then the acceleration is purely centripetal, so
\[|a|=\dfrac{v^2}{r} \nonumber \]
where \(v\) is the velocity of the electron. Equating force \(|F|\) to \(m_e |a|\), we obtain
\[\dfrac{Ze^2}{4\pi \epsilon_0 r^2}=m_e\dfrac{v^2}{r} \nonumber \]
or
\[\dfrac{Ze^2}{4\pi \epsilon_0}=m_e v^2 r \nonumber \]
or
\[\dfrac{Ze^2 m_e r}{4\pi \epsilon_0}=(m_e vr)^2 \label{1.8.14} \]
The reason for writing the equation this way is that the quantity \(m_e vr\) is the classical orbital angular momentum of the electron. Bohr was familiar with Maxwell's theory of classical electromagnetism and knew that in a classical theory, the orbiting electron should radiate energy away and eventually collapse into the nucleus (Figure 1.8.1 ). He circumvented this problem by following Planck's idea underlying blackbody radiation and positing that the orbital angular momentum \(m_e vr\) of the electron could only take on specific values
\[m_e vr=n\hbar\label{1.8.15} \]
with \(n=1,2,3,...\).
Note that the electron must be in motion, so \(n=0\) is not allowed.
Substituting Equation \(\ref{1.8.15}\) into the Equation \(\ref{1.8.14}\), we find
\[\dfrac{Ze^2 m_e r}{4\pi \epsilon_0}=n^2 (\hbar)^2\label{1.8.16} \]
Equation \ref{1.8.16} implies that orbits could only have certain allowed radii
\[\begin{align}r_n &= \dfrac{4\pi \epsilon_0 \hbar^2}{Ze^2 m_e}n^2 \\[4pt] &=\dfrac{a_0}{Z}n^2 \label{1.8.16B} \end{align} \]
with \(n=1,2,3,...\). The collection of constants has been defined to be \(a_0\)
\[a_0=\dfrac{4\pi \epsilon_0 \hbar^2}{e^2 m_e} \nonumber \]
a quantity that is known as the Bohr radius.
We can also calculate the allowed momenta since \(m_e vr=n\hbar\), and \(p=m_e v\). Thus,
\[\begin{align*}p_n r_n &=n\hbar \\[4pt] p_n &=\dfrac{n\hbar}{r_n}\\[4pt] &=\dfrac{\hbar Z}{a_0 n} \\[4pt] &= \dfrac{Ze^2 m_e}{4\pi \epsilon_0 \hbar n}\end{align*\]
From \(p_n\) and \(r_n\), we can calculate the allowed energies from
\[E_n=\dfrac{p^2_n}{2m_e}-\dfrac{Ze^2}{4\pi \epsilon_0 r_n} \nonumber\]
Substituting in the expressions for \(p_n\) and \(r_n\) and simplifying gives
\[E_n=-\dfrac{Z^2 e^4 m_e}{32\pi^2 \epsilon_{0}^{2}\hbar^2}\dfrac{1}{n^2}=-\dfrac{e^4 m_e}{8 \epsilon_{0}^{2}h^2}\dfrac{Z^2}{n^2} \label{1.8.20} \]
We can redefine a new energy scale by defining the Rydberg as
\[1 \ Ry = \dfrac{e^4 m_e}{8\epsilon_{0}^{2} h^2} =2.18\times 10^{-18} \ J. \nonumber \]
and this simplifies the allowed energies predicted by the Bohr model (Equation \ref{1.8.20}) as
\[E_n=-(2.18\times 10^{-18})\dfrac{Z^2}{n^2} \ J=-\dfrac{Z^2}{n^2} \ R_y \label{1.8.21} \]
Hence, the energy of the electron in an atom also is quantized. Equation \(\ref{1.8.21}\) gives the energies of the electronic states of the hydrogen atom. It is very useful in analyzing spectra to represent these energies graphically in an energy-level diagram. An energy-level diagram has energy plotted on the vertical axis with a horizontal line drawn to locate each energy level (Figure 1.8.4 ).
These turn out to be the correct energy levels, apart from small corrections that cannot be accounted for in this pseudo-classical treatment. Despite the fact that the energies are essentially correct, the Bohr model masks the true quantum nature of the electron, which only emerges from a fully quantum mechanical analysis.
Calculate a value for the Bohr radius using Equation \(\ref{1.8.16}\) to check that this equation is consistent with the value 52.9 pm. What would the radius be for \(n = 1\) in the \(\ce{Li^{2+}}\) ion?
- Answer
-
Starting from Equation \ref{1.8.16} and solving for \(r\):
\[ \begin{align*} \dfrac{Ze^2m_er}{4πϵ_0} &=n^2ℏ^2 \\ r &=\dfrac{4 n^2 \hbar^2 πϵ_0}{Z e^2 m_e} \end{align*} \]
with
- \(e\) is the fundamental charge: \(e=1.60217662 \times 10^{-19}C^2\)
- \(m_e\) is the mass of an electron: \(m_e= 9.10938356 \times 10^{-31}kg\)
- \(\epsilon_o\) is the permittivity of free space: \(\epsilon_o = 8.854 \times 10^{-12}C^2N^{-1}m^{-2}\)
- \(\hbar\) is the reduced planks constant: \(\hbar=1.0546 \times 10^{-34}m^2kg/s\)
For the ground-state of the hydrogen atom: \(Z=1\) and \(n=1\).
\[ \begin{align*} r &=\dfrac{4 \hbar^2 πϵ_0}{e^2m_e} \\ &= \dfrac{4 (1.0546 \times 10^{-34}m^2kg/s)^2 \times π \times 8.854 \times 10^{-12}C^2N^{-1}m^{-2}}{(1.60217662 \times 10^{-19}C)^2(9.10938356 \times 10^{-31}kg)} \\ &=5.29 \times 10^{-11}m = 52.9\, pm\end{align*} \]
For the ground-state of the lithium +2 ion: \(Z=3\) and \(n=1\)
\[ \begin{align*} r &=\dfrac{4 \hbar^2 πϵ_0}{3 e^2m_e} \\ &= \dfrac{4 (1.0546 \times 10^{-34}m^2kg/s)^2 \times π \times 8.854\times10^{-12}C^2N^{-1}m^{-2}}{3(1.60217662 \times 10^{-19}C)^2(9.10938356 \times 10^{-31}kg)} \\ &=1.76 \times 10^{-11}m = 17.6 \,pm\end{align*} \]
As expected, the \(\ce{Li^{2+}}\) has a smaller radius than the \(\ce{H}\) atoms because of the increased nuclear charge.
How do the radii of the hydrogen orbits vary with \(n\)? Prepare a graph showing \(r\) as a function of \(n\). States of hydrogen atoms with \(n = 200\) have been prepared (called Rydberg states). What is the diameter of the atoms in these states?
- Answer
-
This is a straightforward application of Equation of \ref{1.8.16B}. The hydrogen atom has only certain allowable radii and these radii can be predicted from the equation that relates them with each \(n\). Note that the electron must be in motion so \(n = 0\) is not allowed.
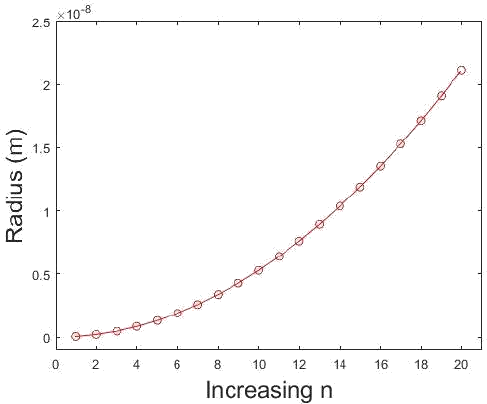
This plot shows the relationship of radius as a function of \(n\). Note that at \(n=1\) the radius is not zero. (CC BY-NC; Ümit Kaya via LibreTexts) \(4 \pi \epsilon_{0}=1.113 \times 10^{-10} \mathrm{C}^{2} \mathrm{J}^{-1} \mathrm{m}^{-1}\) and \(\hbar=1.054 \times 10^{-34} \mathrm{J} \mathrm{s},\) also knowing
\[\begin{aligned}
e &=1.602 \times 10^{-19} \mathrm{C} \text { with } \\
m_{e} &=9.109 \times 10^{-31} \mathrm{kg}
\end{aligned} \nonumber \]and \(Z\) is the nuclear charge, we use this equation directly. A simplification can be made by taking advantage of the fact that
\[a_{0}=\frac{4 \pi \epsilon_{0} \hbar^{2}}{e^{2} m_{e}} \nonumber \]
resulting in
\[r_{n}=\frac{a_{0}}{Z} n^{2} \nonumber \]
where \(a_{0}=5.292 \times 10^{-11} \mathrm{m}\) which is the Bohr Radius.
Suppose we want to find the radius where \(n=200 . n^{2}=40000\) so plugging in directly we have
\[ \begin{align*} r_{n} &=\frac{\left(5.292 \times 10^{-11}\right)}{(1)}(40000) \\[4pt] &=2.117 \times 10^{-6} m \end{align*} \]
for the radius of a hydrogen atom with an electron excited to the \(\mathrm{n}=200\) state. The diameter is then \(4.234 \times 10^{-6} \mathrm{m}\).
The Wave Argument for Quantization
The above discussion is based off of a classical picture of an orbiting electron with the quantization from the angular momentum (Equation \(\ref{1.8.15}\)) requirement lifted from Planck's quantization arguments. Hence, only allows certain trajectories are stable (with differing radii). However, as discussed previously, the electron will have a wavelike property also with a de Broglie wavelength \(\lambda\)
\[\lambda = \dfrac{h}{p} \nonumber \]
Hence, a larger momentum \(p\) implies a shorter wavelength. That means as \(n\) increases (Equation \(\ref{1.8.21}\)), the wavelength must also increase; this is a common feature in quantum mechanics and will be often observed. In the Bohr atom, the circular symmetry and the wave property of the electron requires that the electron waves have an integer number of wavelengths (Figure \(\PageIndex{1A}\)). If not, then the waves will overlap imperfectly and cancel out (i.e., the electron will cease to exist) as demonstrated in Figure \(\PageIndex{1B}\).
A more detailed discussion of the effect of electron waves in atoms will be discuss in the following chapters.
Derivation of the Rydberg Equation from Bohr Model
Given a prediction of the allowed energies of a system, how could we go about verifying them? The general experimental technique known as spectroscopy permits us to probe the various differences between the allowed energies. Thus, if the prediction of the actual energies, themselves, is correct, we should also be able to predict these differences. Let us assume that we are able to place the electron in Bohr's hydrogen atom into an energy state \(E_n\) for \(n>1\), i.e. one of its so-called excited states. The electron will rapidly return to its lowest energy state, known as the ground state and, in doing so, emit light. The energy carried away by the light is determined by the condition that the total energy is conserved (Figure 1.8.6 ).
Thus, if \(n_i\) is the integer that characterizes the initial (excited) state of the electron, and \(n_f\) is the final state (here we imagine that \(n_f =1\), but is applicable in cases that \(n_f <n_i\), i.e., emission)
\[E_{nf}=E_{ni}-h\nu \nonumber \]
or
\[\nu=\dfrac{E_{ni}-E_{nf}}{h}=\dfrac{Z^2 e^4 m_e}{8\epsilon_{0}^{2} h^3}\left ( \dfrac{1}{n_{f}^{2}}-\dfrac{1}{n_{i}^{2}}\right ) \label{1.8.23} \]
We can now identify the Rydberg constant \(R_H\) with the ratio of constants on the right hand side of Equation \(\ref{1.8.23}\)
\[ R_H = \dfrac {m_ee^4}{8 \epsilon ^2_0 h^3 } \nonumber\]
Evaluating \(R_H\) from the fundamental constants in this formula gives a value within 0.5% of that obtained experimentally from the hydrogen atom spectrum.
Thus, by observing the emitted light, we can determine the energy difference between the initial and final energy levels, which results in the emission spectra discussed in Sections 1.4 and 1.5. Different values of \(n_f\) determine which emission spectrum is observed, and the examples shown in the figure are named after the individuals who first observed them. The figure below shows some of the transitions possible for different \(n_f\) and \(n_i\) values discussed previously.
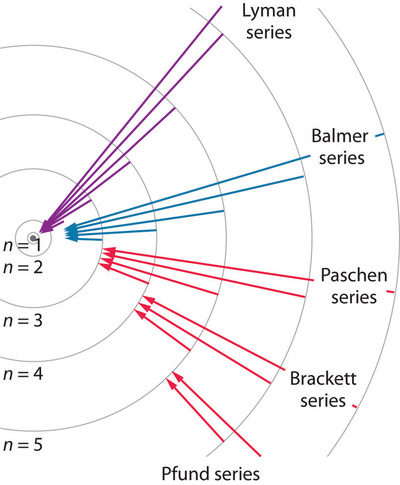
If the atom absorbs light it ends up in an excited state as a result of the absorption. The absorption is only possible for light of certain frequencies, and again, conservation of energy determines what these frequencies are. If light is absorbed, then the final energy \(E_{nf}\) will be related to the initial energy \(E_{ni}\) with \(n_f >n_i\) by
\[E_{nf}=E_{ni}+h\nu \nonumber \]
or
\[\nu=\dfrac{E_{nf}-E_{ni}}{h}=\dfrac{Z^2 e^4 m_e}{8\epsilon_{0}^{2}h^3}\left ( \dfrac{1}{n_{i}^{2}}-\dfrac{1}{n_{f}^{2}}\right ) \nonumber \]
Exercise 1.8.3
- Calculate the energy of a photon that is produced when an electron in a hydrogen atom goes from an orbit with \(n = 4\) to an orbit with \(n = 1\).
- What happens to the energy of the photon as the initial value of \(n\) approaches infinity?
- Answer
-
a:
\[\begin{align*}
E_{\text{nf}} &= E_{ni} - h\nu \\
E_{photon} = h\nu &= E_{nf} - E_{ni}\\
&= \frac{Z^2e^4m_e}{8\epsilon_o^2h^2}\left(\frac{1}{n_f^2} - \frac{1}{n_i^2} \right)\\
&=\frac{e^4m_e}{8\epsilon_o^2h^2}\left(\frac{1}{1^2} - \frac{1}{4^2}\right)\\
&=2.18 \times 10^{-18}\left(1 - \frac{1}{16} \right)\\
&=2.04 \times 10^{-18} J
\end{align*} \]b:
As \(n_i \rightarrow \infty\)
\[\begin{align*}
E_{photon} &= \frac{e^4m_e}{8\epsilon_o^2h^2}\left(\frac{1}{n_f^2} - \frac{1}{n_i^2}\right)\\
\frac{1}{n_i^2} &\rightarrow 0\\
E_{photon} &\rightarrow \frac{e^4m_e}{8\epsilon_o^2h^2}\left(\frac{1}{n_f^2}\right)\\
\end{align*} \]
Bohr’s proposal explained the hydrogen atom spectrum, the origin of the Rydberg formula, and the value of the Rydberg constant. Specifically it demonstrated that the integers in the Rydberg formula are a manifestation of quantization. The energy, the angular momentum, and the radius of the orbiting electron all are quantized. This quantization also parallels the concept of stable orbits in the Bohr model. Only certain values of \(E\), \(M\), and \(r\) are possible, and therefore the electron cannot collapse onto the nucleus by continuously radiating energy because it can only have certain energies, and it cannot be in certain regions of space. The electron can only jump from one orbit (quantum state) to another. The quantization means that the orbits are stable, and the electron cannot spiral into the nucleus in spite of the attractive Coulomb force.
Although Bohr’s ideas successfully explained the hydrogen spectrum, they failed when applied to the spectra of other atoms. In addition a profound question remained. Why is angular momentum quantized in units of \(\hbar\)? As we shall see, de Broglie had an answer to this question, and this answer led Schrödinger to a general postulate that produces the quantization of angular momentum as a consequence. This quantization is not quite as simple as proposed by Bohr, and we will see that it is not possible to determine the distance of the electron from the nucleus as precisely as Bohr thought. In fact, since the position of the electron in the hydrogen atom is not at all as well defined as a classical orbit (such as the moon orbiting the earth) it is called an orbital. An electron orbital represents or describes the position of the electron around the nucleus in terms of a mathematical function called a wavefunction that yields the probability of positions of the electron.
Contributors and Attributions
David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski ("Quantum States of Atoms and Molecules")
- Template:Contriboundless

