27: Molecular Orbitals with higher Energy Atomic Orbitals (Extra Lecture)
- Page ID
- 96068
MOs from higher lying atomic orbitals
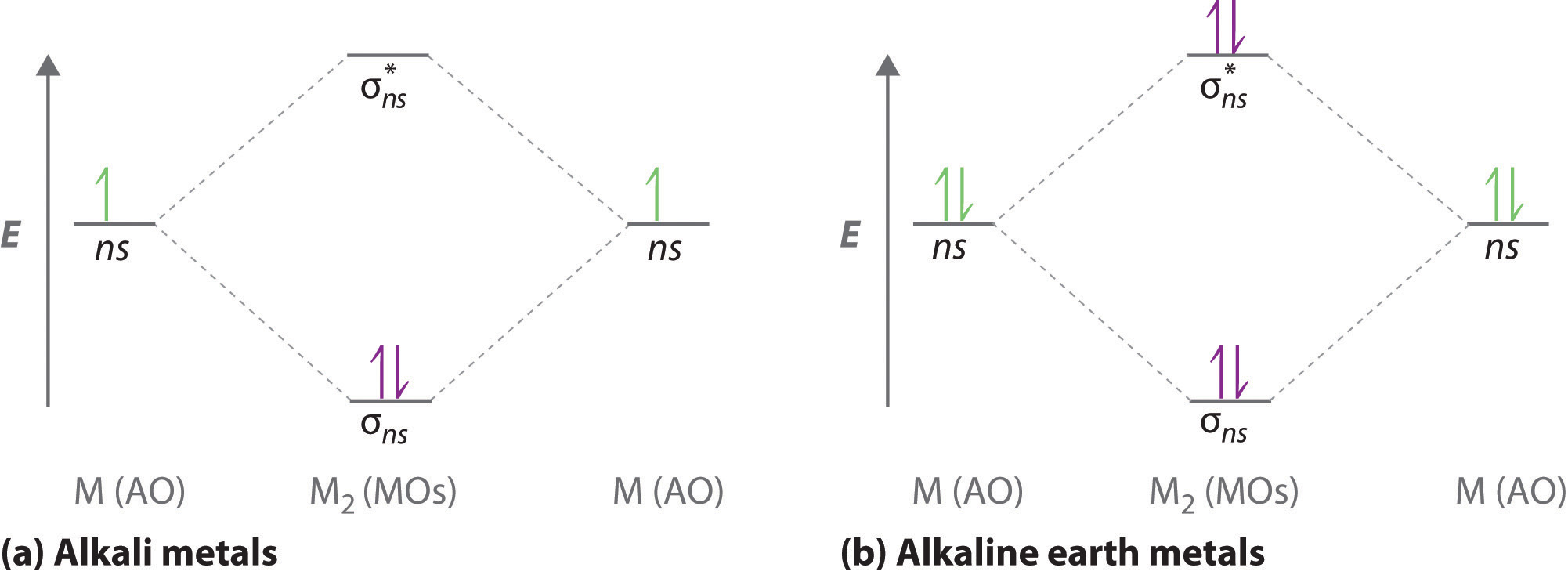
The molecular orbitals diagrams formatted for the dihydrogen species are similar to the diagrams to any homonuclear diatomic molecule with two identical alkali metal atoms (Li2 and Cs2, for example)
Atomic orbitals other than ns orbitals can also interact to form molecular orbitals. Because individual p, d, and f orbitals are not spherically symmetrical, however, we need to define a coordinate system so we know which lobes are interacting in three-dimensional space.
Sigma Bonding from np Orbitals
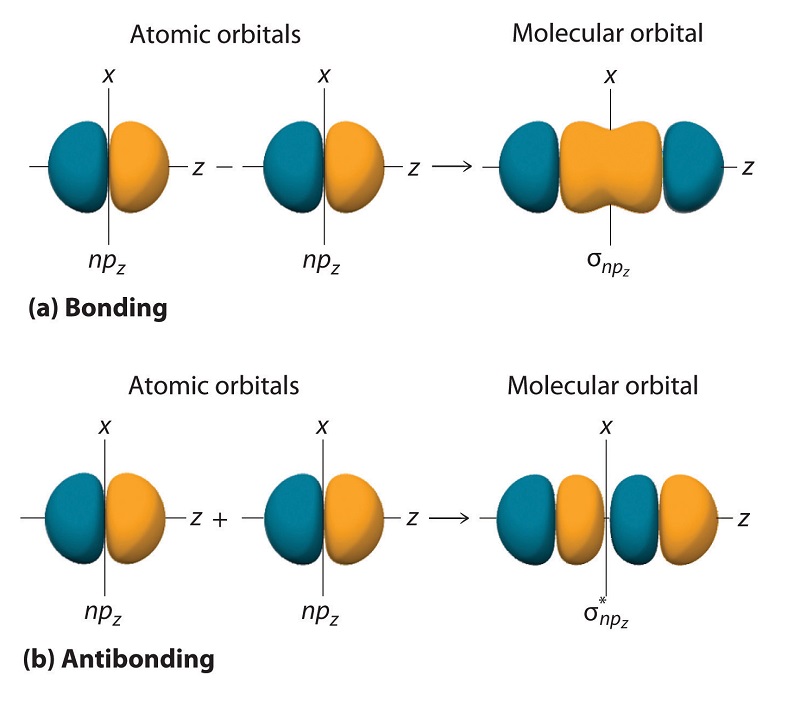
Just as with ns orbitals, we can form molecular orbitals from np orbitals by taking their mathematical sum and difference.
\[ \sigma _{np_{z}}=np_{z}\left ( A \right )-np_{z}\left ( B \right ) \label{9.7.2}\]
The other possible combination of the two npz orbitals is the mathematical sum:
\[ \sigma _{np_{z}}=np_{z}\left ( A \right )+np_{z}\left ( B \right ) \label{9.7.3}\]
Pi bonding from np Orbitals
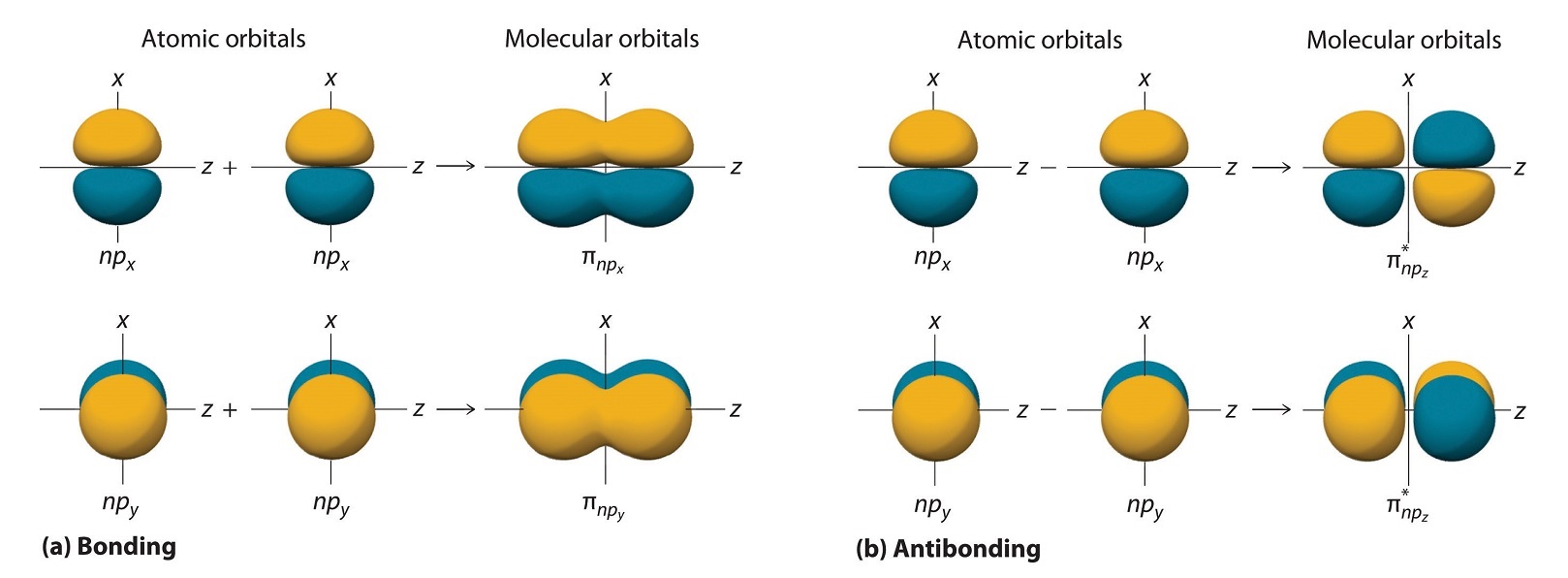
The remaining p orbitals on each of the two atoms, npx and npy, do not point directly toward each other. Instead, they are perpendicular to the internuclear axis. The npx orbital on one atom can interact with only the npx orbital on the other, and the npy orbital on one atom can interact with only the npy on the other. These interactions are side-to-side rather than the head-to-head interactions characteristic of σ orbitals. Each pair of overlapping atomic orbitals again forms two molecular orbitals: one corresponds to the arithmetic sum of the two atomic orbitals and one to the difference.
The sum of these side-to-side interactions increases the electron probability in the region above and below a line connecting the nuclei, so it is a bonding molecular orbital that is called a pi (π) orbital (a bonding molecular orbital formed from the side-to-side interactions of two or more parallel np atomic orbitals). The difference results in the overlap of orbital lobes with opposite signs, which produces a nodal plane perpendicular to the internuclear axis; hence it is an antibonding molecular orbital, called a pi star (π*) orbital An antibonding molecular orbital formed from the difference of the side-to-side interactions of two or more parallel np atomic orbitals, creating a nodal plane perpendicular to the internuclear axis..
\[ \pi _{np_{x}}=np_{x}\left ( A \right )+np_{x}\left ( B \right ) \label{9.7.4}\]
\[ \pi ^{\star }_{np_{x}}=np_{x}\left ( A \right )-np_{x}\left ( B \right ) \label{9.7.5}\]
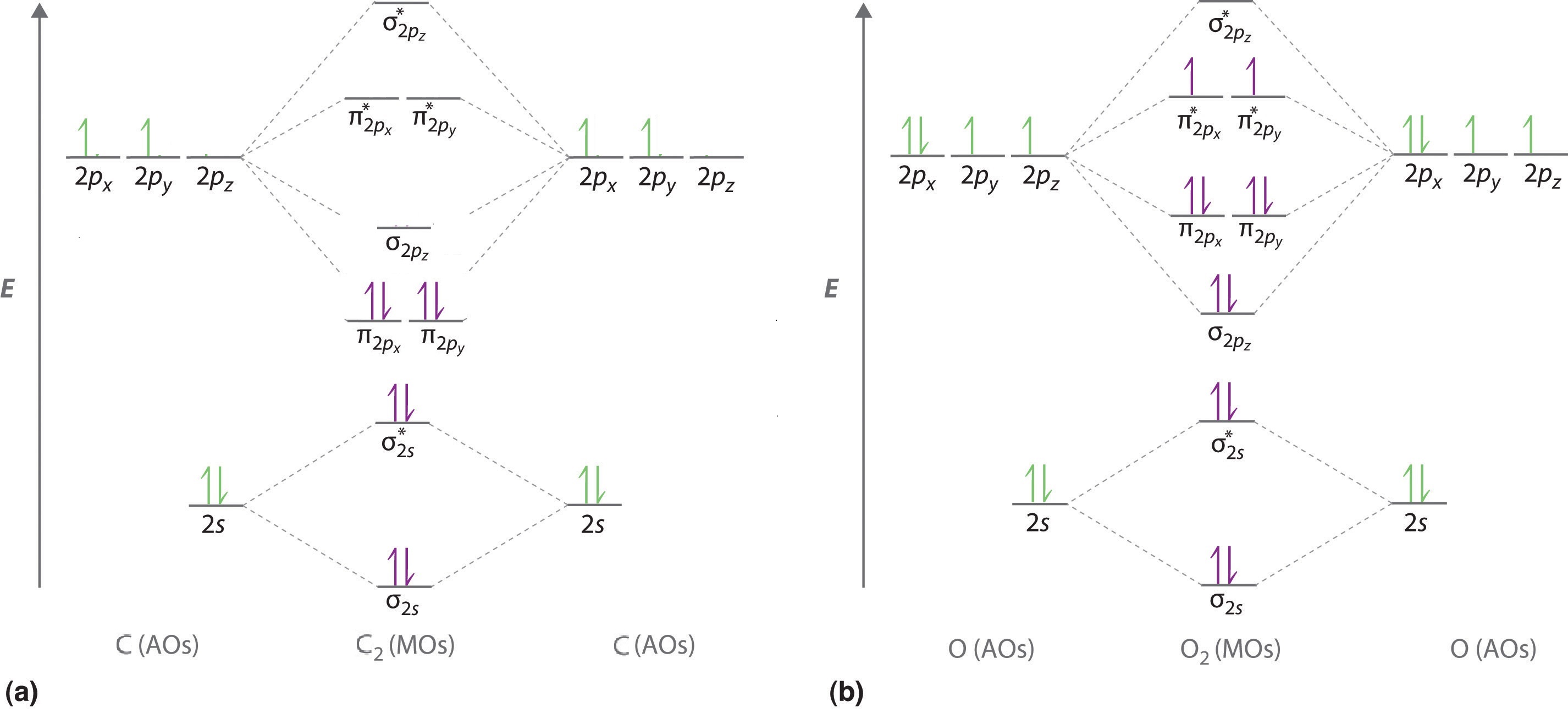
Although many combinations of atomic orbitals form molecular orbitals, we will discuss only one other interaction: an ns atomic orbital on one atom with an npz atomic orbital on another. The sum of the two atomic wave functions (ns + npz) produces a σ bonding molecular orbital. Their difference (ns − npz) produces a σ* antibonding molecular orbital, which has a nodal plane of zero probability density perpendicular to the internuclear axis.

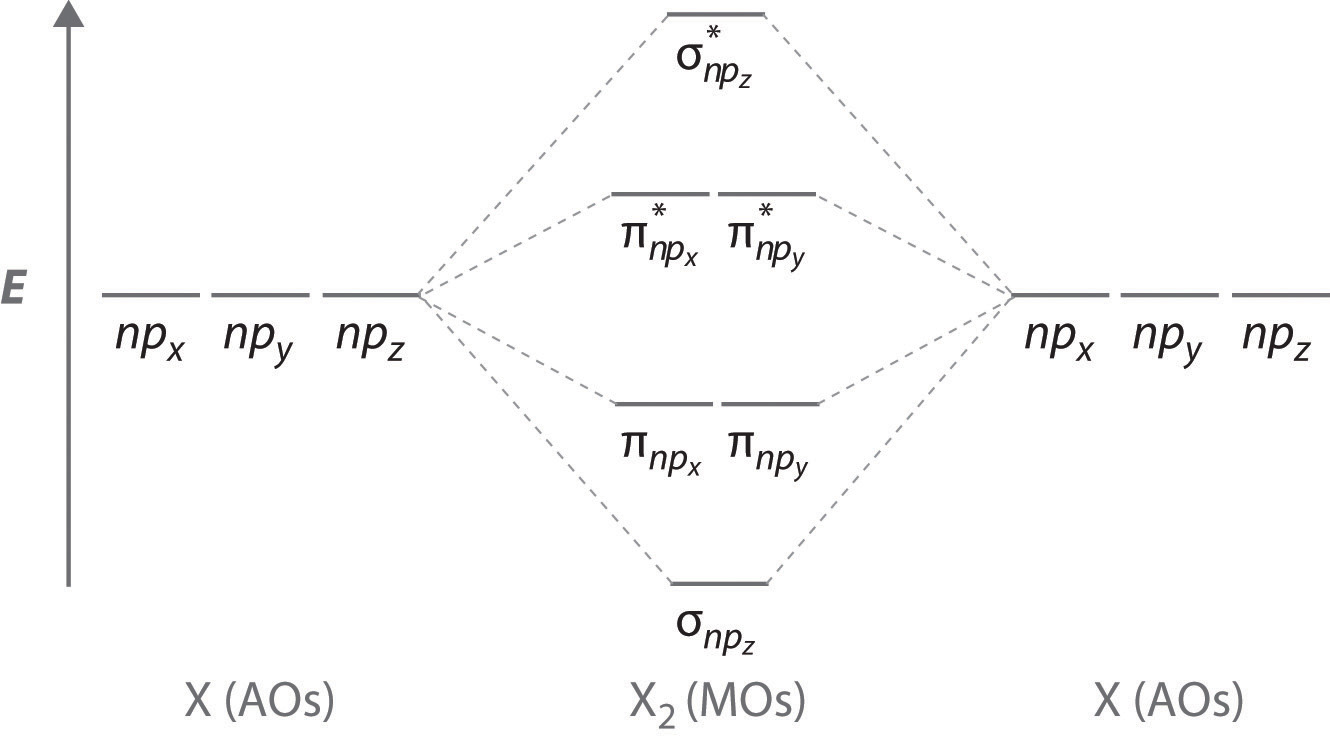
Energies of Molecular Orbitals from p atomic orbitals
The energies of all orbitals vary with intermolecular distance (\(R\)).
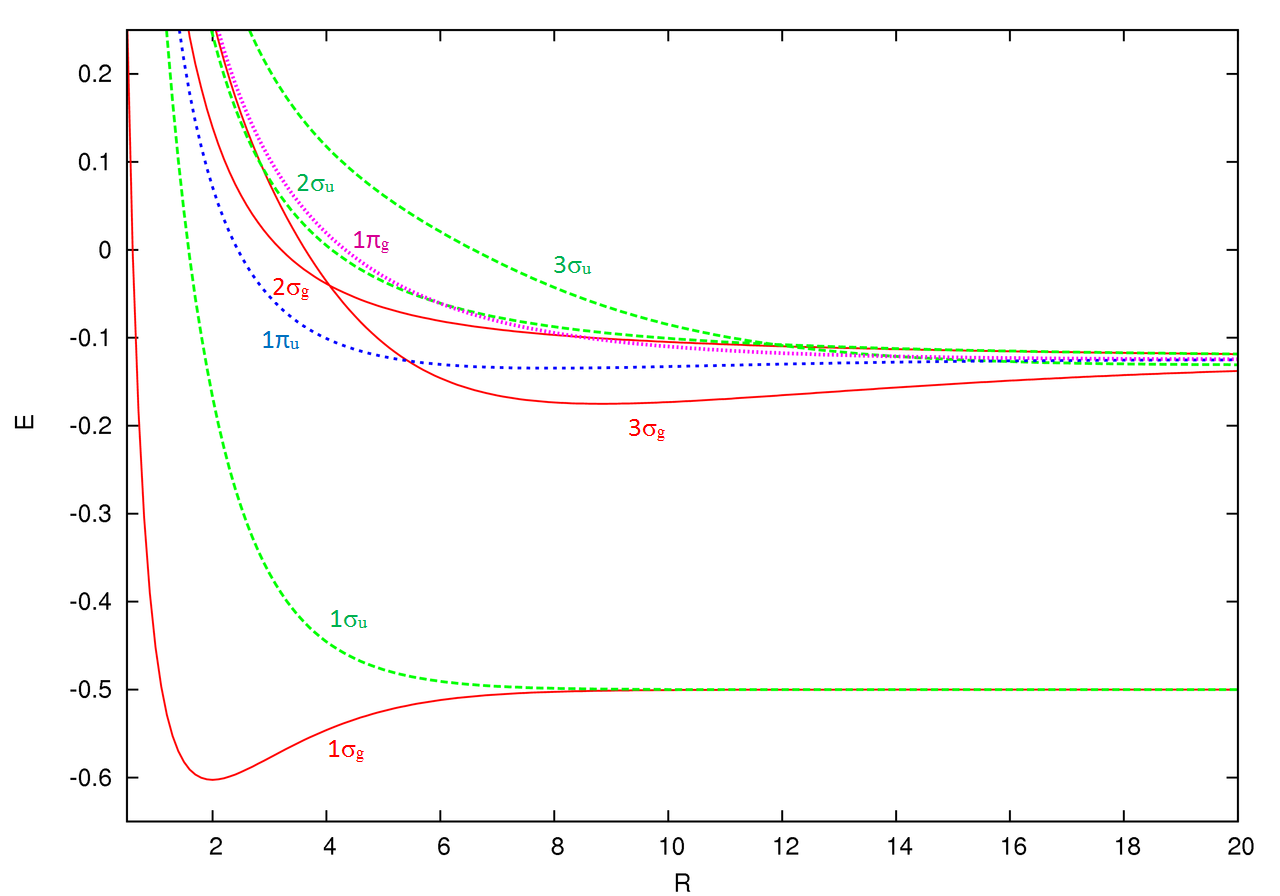
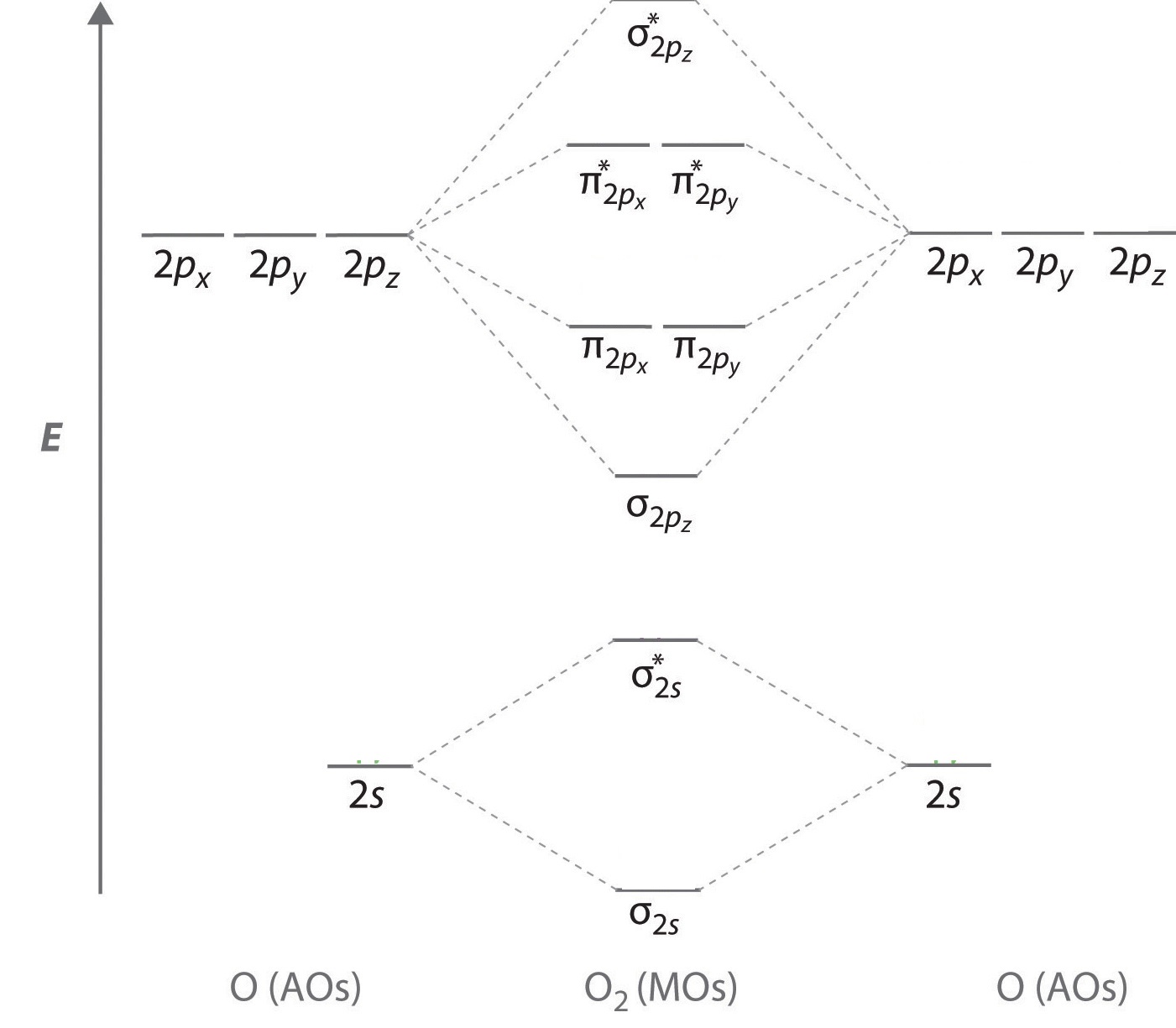
We now describe examples of systems involving period 2 homonuclear diatomic molecules, such as N2, O2, and F2. When we draw a molecular orbital diagram for a molecule, there are four key points to remember:
- The number of molecular orbitals produced is the same as the number of atomic orbitals used to create them.
- As the overlap between two atomic orbitals increases, the difference in energy between the resulting bonding and antibonding molecular orbitals increases.
- When two atomic orbitals combine to form a pair of molecular orbitals, the bonding molecular orbital is stabilized about as much as the antibonding molecular orbital is destabilized.
- The interaction between atomic orbitals is greatest when they have the same energy.
The "Great Sigma-Pi Switchover"
An energy-level diagram that can be applied to two identical interacting atoms that have three np atomic orbitals each.
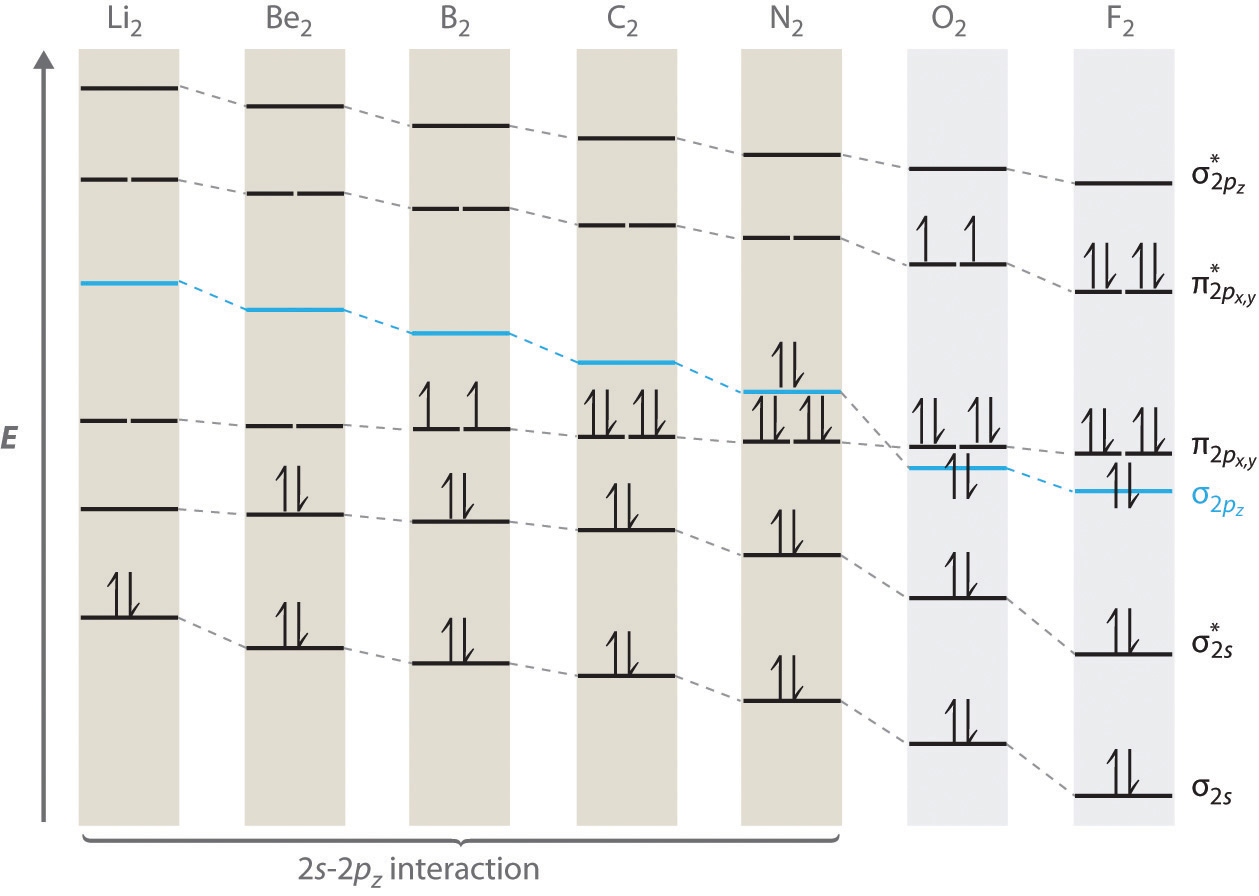
Molecular Oxygen is Paramagnetic
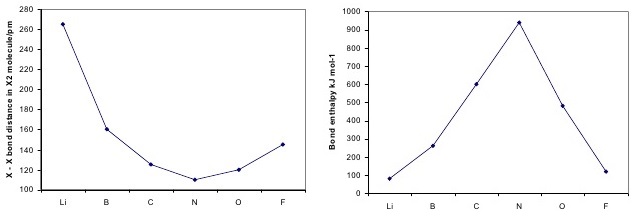
Both bond length and bond energy changes as the bond order increases and as the number of electrons shared between two atoms in a molecule increases, the bond order of a bond increases, the strength of the bond increases and the distance between nuclei decreases:
| Bond | Bond Order | Bond Enthalpy (kJ/mol) | Bond Length (Å) |
|---|---|---|---|
| \(\ce{C-C}\) | 1 | 348 | 1.54 |
| \(\ce{C=C}\) | 2 | 614 | 1.34 |
| \(\ce{C#C}\) | 3 | 839 | 1.20 |
| \(\ce{N-N}\) | 1 | 163 | 1.47 |
| \(\ce{N=N}\) | 2 | 418 | 1.24 |
| \(\ce{N#N}\) | 3 | 941 | 1.10 |
The above trend can be observed in the first row diatomics in Figure \(\PageIndex{1}\). The bond order can be determined directly form the molecular orbital electron configurations.
\[\text{bond order} = \dfrac{\text{number of electrons in bonding MOs}- \text{number of electrons in antbonding MOs}}{2} \label{BO}\]
For diatomics, the occupations can correlate to bond length, bond energies and behavior in applied magnetic fields Figure \(\PageIndex{1}\).
Arrange the following four molecular oxygen species in order of increasing bond length: \(O_2^+\), \(O_2\), \(O_2^-\), and \(O_2^{2-}\).
Solution
The bond length in the oxygen species can be explained by the positions of the electrons in molecular orbital theory.
The bond order is determined from the the electron configurations via Equation \(\ref{BO}\). The electron configurations for the four species are contrasted below.
- \(O_2\): 12 Electrons
-
To obtain the molecular orbital energy-level diagram for O2, we need to place 12 valence electrons (6 from each O atom) in the energy-level diagram shown in Figure \(\PageIndex{1}\). We again fill the orbitals according to Hund’s rules and the Pauli principle, beginning with the orbital that is lowest in energy. Two electrons each are needed to fill the σ2s and σ2s* orbitals, two more to fill the \( \sigma _{2p_{z}} \) orbital, and 4 to fill the degenerate \( \pi _{2p_{x}}^{\star } \) and \( \pi _{2p_{y}}^{\star } \) orbitals. According to Hund’s first rule, the last 2 electrons must be placed in separate \(π^*\) orbitals with their spins parallel, giving a multiplicity of 3 (a triplet state) with two unpaired electrons. This leads to a predicted bond order of
\[\dfrac{8 − 4}{2} = 2 \nonumber\]
which corresponds to a double bond, in agreement with experimental data: the O–O bond length is 120.7 pm, and the bond energy is 498.4 kJ/mol at 298 K.
\[σ_{1s}^2 {σ^*_{1s}}^2 σ_{2s}^2 {σ^*_{2s}}^2 σ_{2p}^2 π_{2p_y}^2 {π^*_{2p_y}}^2 π_{2p_x}^1 {π^*_{2p_y}}^1 \nonumber \]
From the equation above the bond order for \(O_2\) is 2 (i.e., a double bond).
- \(O_2^{+}\): 11 Electrons
-
\[σ_{1s}^2 {σ^*_{1s}}^2 σ_{2s}^2 {σ^*_{2s}}^2 σ_{2p}^2 π_{2p_y}^2 {π^*_{2p_y}}^2 π_{2p_x}^1 {π^*_{2p_y}}^0 \nonumber \]
From the equation above the bond order for \(O_2^{+}\) is 2.5.
- \(O_2^{-}\): 13 Electrons
-
\[σ_{1s}^2 {σ^*_{1s}}^2 σ_{2s}^2 {σ^*_{2s}}^2 σ_{2p}^2 π_{2p_y}^2 {π^*_{2p_y}}^2 π_{2p_x}^1 {π^*_{2p_y}}^2 \nonumber \]
From the equation above the bond order for \(O_2^{-}\) is 1.5.
- \(O_2^{2-}\): 14 Electrons
-
\[σ_{1s}^2 {σ^*_{1s}}^2 σ_{2s}^2 {σ^*_{2s}}^2 σ_{2p}^2 π_{2p_y}^2 {π^*_{2p_y}}^2 π_{2p_x}^2 {π^*_{2p_y}}^2 \nonumber \]
From the equation above the bond order for \(O_2^{2-}\) is 1.
The bond order decreases and the bond length increases in the order. The predicted order of increasing bondlength then is \(O_2^+\) < \(O_2\) < \(O_2^-\) < \(O_2^{2-}\). This trend is confirmed experimentally with \(O_2^+\) (112.2 pm), \(O_2\) (121 pm), \(O_2^-\) (128 pm) and \(O_2^{2-}\) (149 pm).
Liquid O2 Suspended between the Poles of a Magnet. Because the O2 molecule has two unpaired electrons, it is paramagnetic. Consequently, it is attracted into a magnetic field, which allows it to remain suspended between the poles of a powerful magnet until it evaporates.

