23: Electron Spin, Indistinguishability and Slater Determinants
- Page ID
- 40111
Lecture 21 reviewed the basic steps of perturbation theory including how it applies to the energy and wavefunctions. An example of this theory applied to a perturbation of a harmonic oscillator was given. A reminder of the orbital approximation was discussed (where an N-electron wavefunction can be described as N one-electron orbitals that resemble the hydrogen atom wavefunctions). A consequence of the orbital approximation is the ability to construct electron configurations that are filled by the aufbau principle. However, the aufbau principle is only a guideline and not a hardfast rule.
Now Back to Electrons (The Orbital Approximation again)
The generic multi-electron atom including terms for the additional electrons with a general charge \(Z\); e.g.
\[V(r_1) = -\dfrac {Ze^2}{4 \pi \epsilon _0 r_1}\]
So the electronic Hamiltonian for the multi-electron system becomes
\[\hat {H} = -\dfrac {\hbar ^2}{2m_e} \sum _i^N \nabla ^2_i + \sum _i^N V (r_i) + \sum _{i > j}^N V (r_{ij}) \]
We predict that exact solutions to the multi-electron Schrödinger equation would consist of a family of multi-electron wavefunctions, each with an associated energy eigenvalue, i.e.,
\[|\psi_a (r_1, r_2, \cdots r_N) \rangle\]
with energy \(E_a\) and
\[|\psi_b (r_1, r_2, \cdots r_N) \rangle\]
with energy \(E_b\) and
\[|\psi_c (r_1, r_2, \cdots r_N) \rangle\]
with energy \(E_c\) etc.
The fact that electrons interact through their Coulomb repulsion means that an exact wavefunction for a multi-electron system would be a single function that depends simultaneously upon the coordinates of all the electrons; i.e., a multi-electron wavefunction. These wavefunctions and energies would describe the ground and excited states of the multi-electron atom, just as the hydrogen wavefunctions and their associated energies describe the ground and excited states of the hydrogen atom. We would predict quantum numbers to be involved, as well.
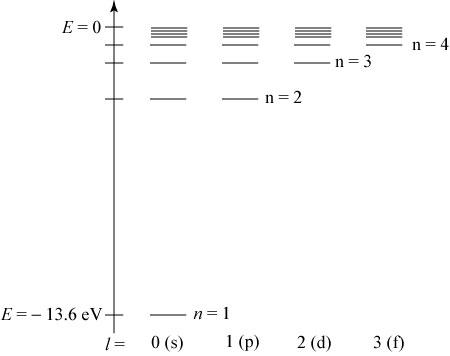
Unfortunately, the Coulomb repulsion terms make it impossible to find an exact solution to the Schrödinger equation for many-electron atoms.
The most basic approximations to the exact solutions involve writing a multi-electron wavefunction as a simple product of single-electron orbitals, and obtaining the energy of the atom in the state described by that wavefunction as the sum of the energies of the one-electron components.
By writing the multi-electron wavefunction as a product of single-electron functions, we conceptually transform a multi-electron atom into a collection of individual electrons located in individual functions whose spatial characteristics and energies can be separately identified. For atoms, these single-electron functions are called atomic orbitals.
\[|\psi (r_1, r_2, \cdots , r_i) \rangle \approx |\phi _1 (r_1) \phi _2 (r_2) \cdots \phi _i(r_i)\rangle \label{orbitalapprox}\]
Knowing the orbitals of a particular species provides information about the sizes, shapes, directions, symmetries, and energies of those regions of space that are available to the electrons (i.e., the complete set of orbitals that are available). This knowledge does not determine into which orbitals the electrons are placed. It is by describing the electronic configurations (i.e., orbital occupancies such as \(1s^22s^22p^2\) or \(1s^22s^22p^13s^1\)) appropriate to the energy range under study that one focuses on how the electrons occupy the orbitals (scaled by the effective nuclear charge).

Using the information from the figure above it is possible to arrange the orbitals in an order that approximately reflects increasing energy which is useful to figure out the orbital occupancies using a few simple rules.
So unfortunately, it seems that even though most of the effects which combine to result in the observed electronic configurations are known, there is no qualitative way to predict where the configurations are going to mismatch with the aufbau principle or the energy levels of the orbitals. The aufbau principle is most decidedly wrong for practically every atom with respect to the placement of the orbital energy levels, but incredibly it happens to predict the configuration of the valence shell for most atoms.
Electron Spin
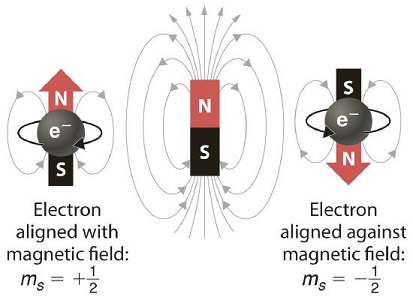
In 1920, Otto Stern and Walter Gerlach designed an experiment, which unintentionally led to the discovery that electrons have their own individual, continuous spin even as they move along their orbital of an atom. The result was that silver atoms formed a beam that passed through a magnetic field in which it split in two.
Stern–Gerlach experiment: silver atoms travel through an inhomogeneous magnetic field and are deflected up or down depending on their spin.
We need a charged particle with angular momentum to produce a magnetic moment, just like that obtained by the orbital motion of the electron. We can postulate that our observation results from a motion of the electron that was not considered in the last section - electron spin.
Electronic Configurations
Specification of a particular occupancy of the set of orbitals available to the system gives an electronic configuration.
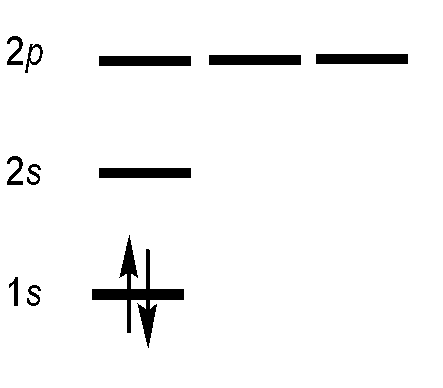
Helium Atom
The helium atom has the \(1s^2\) electronic configuration (and the \(\ce{Li^{+} }\) ions). This configuration can describe a single spinorbital:
\[ | 1s(1)\uparrow 1s(2) \downarrow \rangle \quad \text{or} \quad | 1s(1)\alpha 1s(2) \beta \rangle \nonumber \]
Within the orbital approximation (Equation \ref{orbitalapprox}) each electron resides is in a spinorbital with an spatial orbital part (involving \(n\), \(l\) and \(m_l\)) quantum numbers and a spin part (involving the \(m_s\) quantum number). We know there are two different values of \(m_s\) from general chemistry.
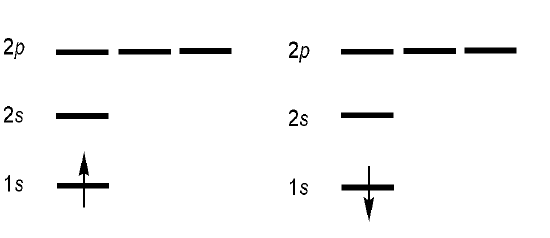
Hydrogen Atom
The hydrogen atom has the \(1s^1\) electronic configuration for the hydrogen atom (and the \(\ce{He^{+1}}\) and the \(\ce{Li^{+2} }\) ions). This configuration can describe two possible spinorbital combinations:
\[ | 1s(1)\uparrow \rangle \quad \text{or} \quad | 1s(1)\alpha \rangle \nonumber \]
or
\[ | 1s(1)\downarrow \rangle \quad \text{or} \quad | 1s(1)\beta\rangle \nonumber\]
Carbon Atom
- \(1s^22s^22p^2\) is an electronic configuration for the carbon atom (and the \(\ce{N^{+1}}\) and the \(\ce{O^{+2}}\) ions)
This configuration represents situations in which the electrons occupy low-energy orbitals of the system and, as such, are likely to contribute strongly to the true ground and low-lying excited states and to the low-energy states of molecules formed from these atoms or ions.
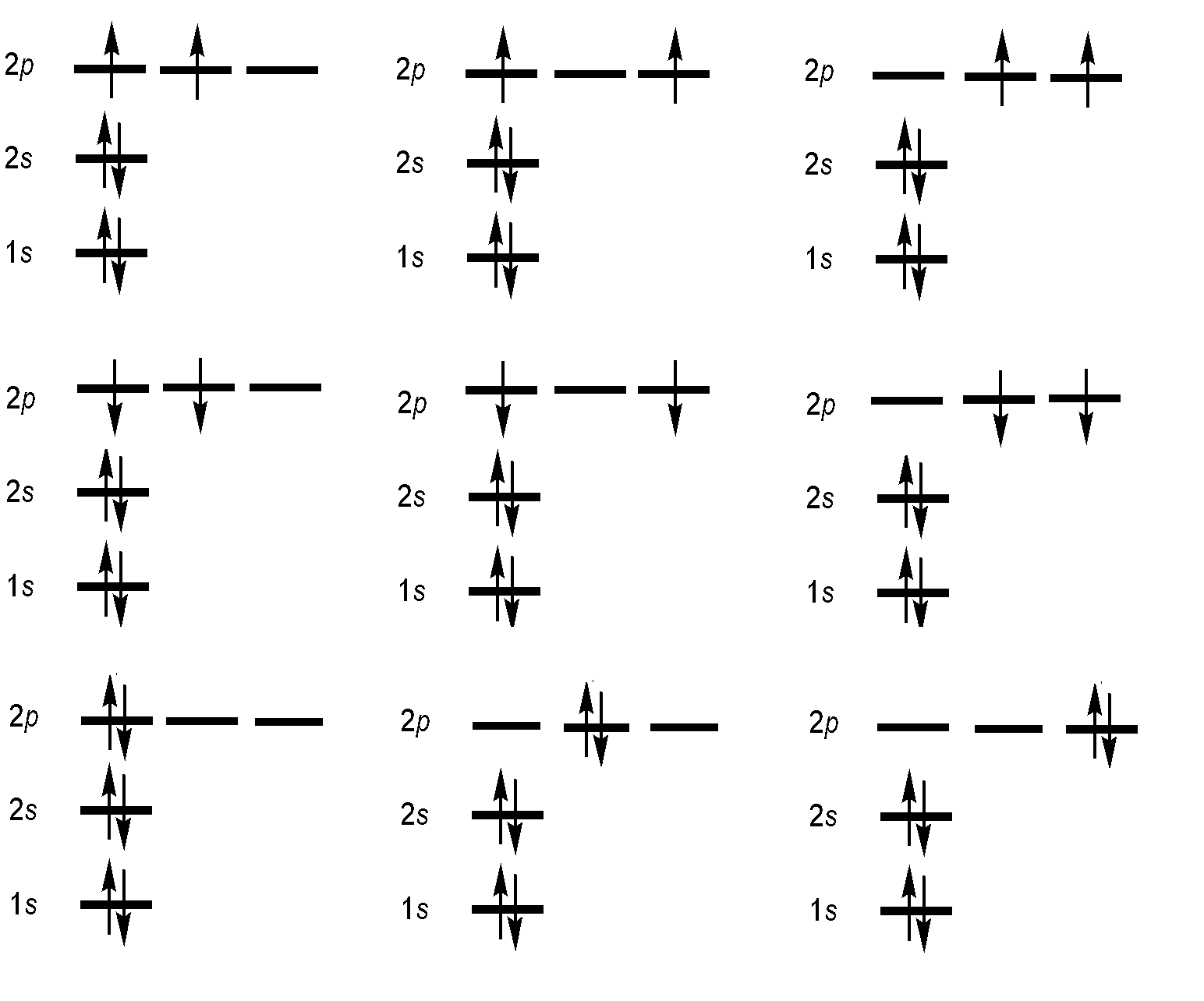
Specification of an electronic configuration does not, however, specify a particular electronic state of the system (i.e., which orbital is occupied). For the electronic configuration of carbon with \(1s^22s^22p^2\), there are many ways in which the 2p orbitals can be occupied by the two electrons. As a result, there are a total of multiple "microstates" which cluster into energetically distinct levels, lying within this single configuration.
To address these levels, we need to discuss electron spin and the fourth Quantum Number!
\(S\) is Analogous to \(L\)
The important feature of the spinning electron is the spin angular momentum vector, which we label \(S\) by analogy with the orbital angular momentum \(L\).
We found for orbital angular momentum
\[ \hat {L}^2 | Y^{m_l} _l \rangle= l(l + 1) \hbar^2 |Y^{m_l}_l\rangle \]
so by analogy for the spin states, we must have spin-angular momentum
\[ \hat {S}^2| \sigma ^{m_s} _s \rangle= s( s + 1) \hbar ^2 | \sigma ^{m_s}_s \rangle\]
where \(\sigma\) is a spin wavefunction with quantum numbers \(s\) and \(m_s\) that obey the same rules as the quantum numbers \(l\) and \(m_l\) associated with the spherical harmonic wavefunction \(Y^{m_l} _l\).
We also found a quantization of the projection of \(\vec{L}\) on the z-axis
\[ \hat {L}_z | Y^{m_l}_l \rangle= m_l \hbar | Y^{m_l}_l \rangle\]
so by analogy, we must have a similar quanitization of \(\vec{S}\)
\[ \hat {S}_z | \sigma ^{m_s}_s \rangle = m_s \hbar |\sigma ^{m_s}_s \rangle\]
Since \(m_l\) ranges in integer steps from \(-l\) to \(+l\), also by analogy \(m_s\) ranges in integer steps from \(-s\) to \(+s\).
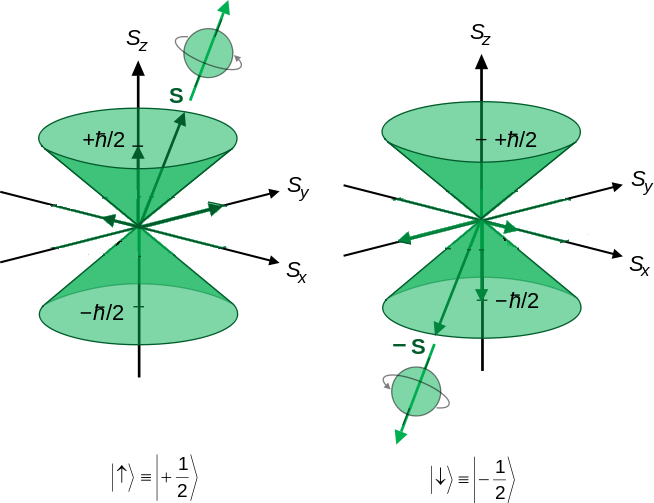
Consequently, the two values of \(m_s\) must be \(+s\) and \(-s\), and the difference in \(m_s\) for the two states, labeled \(f\) and \(i\) below, must be the smallest integer step, i.e. 1. The result of this logic is that
\[\begin{align*} m_{s,f} - m_{s,i} &= 1 (+s) - (-s) \\[4pt] 2s &= 1 \\[4pt] s &= \dfrac {1}{2} \end{align*}\]
the magnitude of the spin quantum number is 1/2 and the values for \(m_s\) are +1/2 and -1/2.
Hence, the magnitude of the z-component of spin angular momentum, \(S_z\), is given by
\[S_z = m_s \hbar \label {8.4.6}\]
so the value of \(S_z\) is \(+ħ/2\) for spin state \(\alpha\) and \(-ħ/2\) for spin state \(\beta\).
Since s = 1/2, then the multiplicity (degeneracy) associated with a single electron spin would be 2s+1=2 (like in orbital angular momenta). This is why we draw arrow to represent electrons in configurations as either up or down.
Electron's hypothetical surface would have to be moving faster than the speed of light for it to rotate quickly enough to produce the observed angular momentum. Hence, an electron is not simply a spinning ball or ring and electron spin appears to be an intrinsic angular moment of the particle rather than a consequence of its rotation.
Even though we do not know their functional forms, the spin wavefunctions are taken to be normalized and orthogonal to each other.
\[ \langle \alpha | \alpha \rangle = \langle \beta | \beta \rangle =1 \]
and
\[ \langle \alpha | \beta \rangle = \langle \beta| \alpha \rangle = 0 \]
where the integral is over the spin variable \(\tau _s\).
Complete the Quantum Number Tetrad: spin-orbitals
Hydrogenic spin-orbitals used as components of multi-electron systems are identified in the same way as they are for the hydrogen atom. Each spin-orbital consists of a spatial wavefunction, specified by the the quantum numbers (\(n\), \(\ell\), and \(m_\ell\)) and denoted 1s, 2s, 2p, 3s, 3p, 3d, etc, multiplied by a spin function, specified by the quantum number ms and denoted \(\alpha\) or \(\beta\).
The subscript on the argument of the spatial function reveals which electron is being described (\(r_1\) is a vector that refers to the coordinates of electron 1, for example.) No argument is given for the spin function. An example of a spin-orbital for electron 2 in a \(3p_z\) orbital:
\[ | \phi _{3p_z} \alpha (r_2) \rangle = \phi _{3,1,0}(r_2) \alpha \]
The basic mathematical functions and thus the general shapes and angular momenta for hydrogenic orbitals are the same as those for hydrogen orbitals.
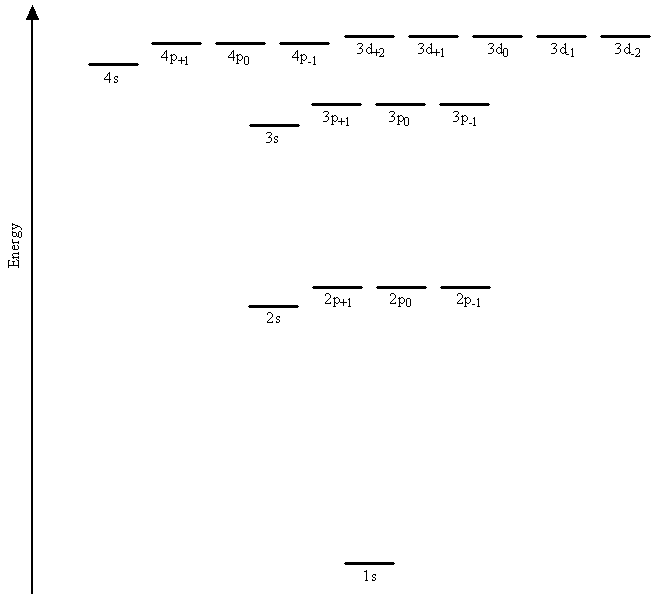
The energy of each electron now depends not only on its principle quantum number, \(n\), but also on its angular momentum quantum number, \(\ell\).
Pauli Exclusion Principle
Three rules apply for predicting the ground state configuration of an atom:
- The Pauli Exclusion Principle: There is one more quantum number called the spin quantum number \(m_s\) that can take values +½ or -½ (for electrons). No two electrons can have the same four quantum numbers so an orbital can "hold" only two electrons. (i.e., only two electrons can be described by the same spacial wave function). This rule cannot be broken.
- The Aufbau principle: Electron configurations are built up by filling the lowest energy orbitals first (provided the energy differences are significant). Remember this rule applies to the ground state; excited configurations that do not violate the Pauli principle are possible.
- Hund's (first) rule: Where orbitals have the same energy (are degenerate) or nearly so, they will be filled one electron in each, with parallel spins, before pairing begins. Other configurations are excited states, i.e., not forbidden.
The mathematical analog of these steps is the construction of the approximate multi-electron wavefunction as a product of the single-electron "atomic" spin-orbitals. For example, the configuration of the boron atom, shown schematically in the energy level diagram, is written in shorthand form as 1s22s22p1. The degeneracy of the 2s and 2p orbitals is broken by the electron-electron interactions in multi-electron systems.
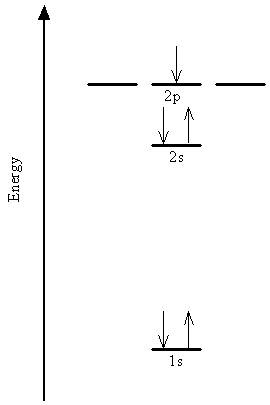
Rather than showing the individual spin-orbitals in the diagram or in the shorthand notation, we commonly say that up to two electrons can be described by each spatial orbital, one with spin function \(\alpha\) (electron denoted by an arrow pointing up) and the other with spin function \(\beta\) (arrow pointing down). This restriction is a manifestation of the Pauli Exclusion Principle mentioned above.
Indistinguishability
We will use the following statement as a guide to keep our explorations focused on the development of a clear picture of the multi-electron atom: “When a multi-electron wavefunction is built as a product of single-electron wavefunctions, the corresponding concept is that exactly one electron’s worth of charge density is described by each atomic spin-orbital.”
A subtle, but important part of the conceptual picture is that the electrons in a multi-electron system are not distinguishable from one another by any experimental means. Since the electrons are indistinguishable, the probability density we calculate by squaring the modulus of our multi-electron wavefunction also cannot change when the electrons are interchanged (permuted) between different orbitals. In general, if we interchange two identical particles, the world does not change. As we will see below, this requirement leads to the idea that the world can be divided into two types of particles based on their behavior with respect to permutation or interchange.
We could symbolically write an approximate two-particle wavefunction as \(|\psi (r_1, r_2) \rangle\). This could be, for example, a two-electron wavefunction for helium. To exchange the two particles, we simply substitute the coordinates of particle 1 (\(r_1\)) for the coordinates of particle 2 (\(r_2\)) and vice versa, to get the new wavefunction \(|\psi (r_1, r_2) \rangle\). This new wavefunction must have the property that
\[ \begin{align*} |\psi (r_1, r_2)|^2 &= \psi (r_2, r_1)^*\psi (r_2, r_1) \\[4pt] &= \psi (r_1, r_2)^* \psi (r_1, r_2) \end{align*}\]
This will be true only if the wavefunctions before and after permutation are related by a factor of \(e^{i\phi}\),
\[\psi (r_1, r_2) = e^{i\phi} \psi (r_2, r_1) \]
so that when squared
\[ \left ( e^{-i\phi} \psi (r_1, r_2) ^*\right ) \left ( e^{i\phi} \psi (r_1, r_2) ^*\right ) = \psi (r_1 , r_2 ) ^* \psi (r_1 , r_2) \label {9-40}\]
If we exchange or permute two identical particles twice, we are (by definition) back to the original situation. If each permutation changes the wavefunction by \(e^{i \phi}\), the double permutation must change the wavefunction by \(e^{i\phi} e^{i\phi}\). Since we then are back to the original state, the effect of the double permutation must equal 1; i.e.,
\[e^{i\phi} e^{i\phi} = e^{i 2\phi} = 1 \]
which is true only if \(\phi = 0 \) or an integer multiple of \(π\). The requirement that a double permutation reproduce the original situation limits the acceptable values for \(e^{i\phi}\) to either +1 (when \(\phi = 0\)) or -1 (when \(\phi = \pi\)). Both possibilities are found in nature.
Bosons (symmetric)
The behavior of some particles requires that the wavefunction be symmetric with respect to permutation \((e^{i\phi} =+1)\). A wavefunction that is symmetric with respect to electron interchange is one whose output does NOT change sign when the electron coordinates are interchanged, as shown below.
\[ \psi (r_2 , r_1) = e^{i\phi} \psi (r_1, r_2) = + \psi (r_1, r_2) \]
These particles are called bosons and have integer spin such as deuterium nuclei, photons, and gluons.
Fermions (antisymmetric)
The behavior of other particles requires that the wavefunction be antisymmetric with respect to permutation \((e^{i\phi} = -1)\). A wavefunction that is antisymmetric with respect to electron interchange is one whose output changes sign when the electron coordinates are interchanged, as shown below.
\[ \psi (r_2 , r_1) = e^{i\phi} \psi (r_1, r_2) = - \psi (r_1, r_2) \]
These particles, called fermions, have half-integer spin and include electrons, protons, and neutrinos.
Blindly following the first statement of the Pauli Exclusion Principle, that each electron in a multi-electron atom must be described by a different spin-orbital, we try constructing a simple product wavefunction for helium using two different spin-orbitals. Both have the 1s spatial component, but one has spin function \(\alpha\) and the other has spin function \(\beta\) so the product wavefunction matches the form of the ground state electron configuration for He, \(1s^2\).
\[ | \psi (\mathbf{r}_1, \mathbf{r}_2 ) \rangle = |\phi _{1s\alpha} (\mathbf{r}_1) \phi _{1s\beta} ( \mathbf{r}_2) \rangle\label{8.6.1}\]
After permutation of the electrons, this becomes
\[| \psi ( \mathbf{r}_2,\mathbf{r}_1 ) \rangle =| \phi _{1s\alpha} ( \mathbf{r}_2) \phi _{1s\beta} (\mathbf{r}_1) \rangle \label{8.6.2}\]
which is different from the starting function since \(\phi _{1s\alpha}\) and \(\phi _{1s\beta}\) are different spin-orbital functions. However, an antisymmetric function must produce the same function multiplied by (–1) after permutation, and that is not the case here.
Mathematically, when we switch the two we want we want (since they are fermions)
\[ | \psi ( \mathbf{r}_2,\mathbf{r}_1 ) \rangle = - | \psi (\mathbf{r}_1, \mathbf{r}_2 ) \rangle \]
and when writing out the wavefunctions:
\[| \phi _{1s\alpha} ( \mathbf{r}_2) \phi _{1s\beta} (\mathbf{r}_1) \rangle \neq - |\phi _{1s\alpha} (\mathbf{r}_1) \phi _{1s\beta} ( \mathbf{r}_2) \rangle\]
Therefore the wavefunction in Equation \ref{8.6.1} is not a good wavefunction. We must try something else.
To avoid getting a totally different function when we permute the electrons, we can make a linear combination of functions. A very simple way of taking a linear combination involves making a new function by simply adding or subtracting functions. The function that is created by subtracting the right-hand side of Equation \(\ref{8.6.2}\) from the right-hand side of Equation \(\ref{8.6.1}\) has the desired antisymmetric behavior. The \(2^{-1/2}\) constant on the left-hand side accounts for the fact that the total wavefunction must be normalized.
\[| \psi (\mathbf{r}_1, \mathbf{r}_2) \rangle = \dfrac {1}{\sqrt {2}} [ \phi _{1s\alpha}(\mathbf{r}_1) \phi _{1s\beta}( \mathbf{r}_2) - \phi _{1s\alpha}( \mathbf{r}_2) \phi _{1s\beta}(\mathbf{r}_1)]\]
Does this satisfy the antisymmetric requirement for electron exchange:
\[| \psi (\mathbf{r}_1, \mathbf{r}_2) \rangle \overset{?}{=} - | \psi (\mathbf{r}_2, \mathbf{r}_1) \rangle \]
\[ \dfrac {1}{\sqrt {2}} [ \phi _{1s\alpha}(\mathbf{r}_1) \phi _{1s\beta}( \mathbf{r}_2) - \phi _{1s\alpha}( \mathbf{r}_2) \phi _{1s\beta}(\mathbf{r}_1)] \overset{?}{=} - \dfrac {1}{\sqrt {2}} [ \phi _{1s\alpha}(\mathbf{r}_2) \phi _{1s\beta}( \mathbf{r}_1) - \phi _{1s\alpha}( \mathbf{r}_1) \phi _{1s\beta}(\mathbf{r}_2)] \]
simplify
\[ \dfrac {1}{\sqrt {2}} [ \phi _{1s\alpha}(\mathbf{r}_1) \phi _{1s\beta}( \mathbf{r}_2) - \phi _{1s\alpha}( \mathbf{r}_2) \phi _{1s\beta}(\mathbf{r}_1)] \overset{\checkmark}{=} + \dfrac {1}{\sqrt {2}} [ \phi _{1s\alpha}(\mathbf{r}_1) \phi _{1s\beta}( \mathbf{r}_2) - \phi _{1s\alpha}( \mathbf{r}_2) \phi _{1s\beta}(\mathbf{r}_1)] \]
Slater Determinants as a way to "Hardwire" Indistinguishability into the Wavefunction
A linear combination that describes an appropriately antisymmetrized multi-electron wavefunction for any desired orbital configuration is easy to construct for a two-electron system. However, interesting chemical systems usually contain more than two electrons. For these multi-electron systems, a relatively simple scheme for constructing an antisymmetric wavefunction from a product of one-electron functions is to write the wavefunction in the form of a determinant. John Slater introduced this idea so the determinant is called a Slater determinant.
The Slater determinant for the two-electron wavefunction of helium is
\[ | \psi (\mathbf{r}_1, \mathbf{r}_2) \rangle = \dfrac {1}{\sqrt {2}} \begin {vmatrix} \phi _{1s} (1) \alpha (1) & \phi _{1s} (1) \beta (1) \\ \phi _{1s} (2) \alpha (2) & \phi _{1s} (2) \beta (2) \end {vmatrix} \label{slater} \]
We can introduce a shorthand notation for the arbitrary spin-orbital
\[ \phi_{i\alpha}(\mathbf{r}) = \phi_i \alpha\]
or
\[ \phi_{i\beta}(\mathbf{r}) = \phi_i \beta\]
as determined by the \(m_s\) quantum number. A shorthand notation for the determinant in Equation \ref{slater} is then
\[ | \psi (\mathbf{r}_1 , \mathbf{r}_2) \rangle = 2^{-\frac {1}{2}} Det | \phi_{1s\alpha} (\mathbf{r}_1) \phi_{1s\beta} ( \mathbf{r}_2) | \]
The determinant is written so the electron coordinate changes in going from one row to the next, and the spin orbital changes in going from one column to the next. The advantage of having this recipe is clear if you try to construct an antisymmetric wavefunction that describes the orbital configuration for uranium! Note that the normalization constant is \((N!)^{-\frac {1}{2}}\) for N electrons.
The generalized Slater determinant for a multi-electron atom with N electrons is then
\[ | \psi(\mathbf{r}_1, \mathbf{r}_2, \ldots, \mathbf{r}_N) \rangle =\dfrac{1}{\sqrt{N!}} \left| \begin{matrix} \phi_1(\mathbf{r}_1) & \phi_2(\mathbf{r}_1) & \cdots & \phi_N(\mathbf{r}_1) \\ \phi_1(\mathbf{r}_2) & \phi_2(\mathbf{r}_2) & \cdots & \phi_N(\mathbf{r}_2) \\ \vdots & \vdots & \ddots & \vdots \\ \phi_1(\mathbf{r}_N) & \phi_2(\mathbf{r}_N) & \cdots & \phi_N(\mathbf{r}_N) \end{matrix} \right| \]

