10.3: Vectors
- Last updated
- Save as PDF
- Page ID
- 143041
In this chapter we will review a few concepts you probably know from your physics courses. This chapter does not intend to cover the topic in a comprehensive manner, but instead touch on a few concepts that you will use in your physical chemistry classes.
A vector is a quantity that has both a magnitude and a direction, and as such they are used to specify the position, velocity and momentum of a particle, or to specify a force. Vectors are usually denoted by boldface symbols (e.g. \(\mathbf{u}\)) or with an arrow above the symbol (e.g. \(\vec{u}\)). A tilde placed above or below the name of the vector is also commonly used in shorthand (\(\widetilde{u}\),\(\underset{\sim}{u}\)).
If we multiply a number \(a\) by a vector \(\mathbf{v}\), we obtain a new vector that is parallel to the original but with a length that is \(a\) times the length of \(\mathbf{v}\). If \(a\) is negative \(a\mathbf{v}\) points in the opposite direction than \(\mathbf{v}\). We can express any vector in terms of the so-called unit vectors. These vectors, which are designated \(\hat{\mathbf{i}}\), \(\hat{\mathbf{j}}\) and \(\hat{\mathbf{k}}\), have unit length and point along the positive \(x, y\) and \(z\) axis of the cartesian coordinate system (Figure \(\PageIndex{1}\)). The symbol \(\hat{\mathbf{i}}\) is read "i-hat". Hats are used to denote that a vector has unit length.
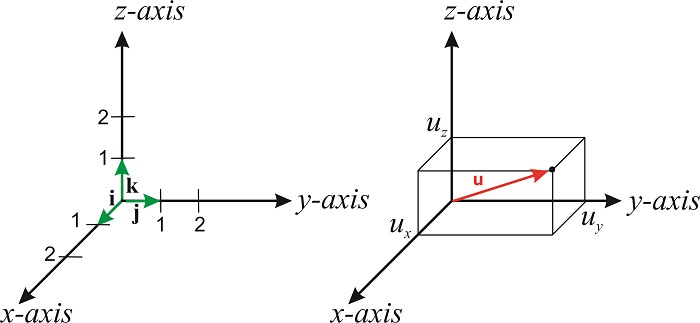
The length of \(\mathbf{u}\) is its magnitude (or modulus), and is usually denoted by \(u\):
\[\label{eq:vectors1} u=|u|=(u_x^2+u_y^2+u_z^2)^{1/2}\]
If we have two vectors \(\mathbf{u}=u_x\hat{\mathbf{i}}+u_y \hat{\mathbf{j}}+u_z \hat{\mathbf{k}}\) and \(\mathbf{v}=v_x \hat{\mathbf{i}}+v_y \hat{\mathbf{j}}+v_z \hat{\mathbf{k}}\), we can add them to obtain
\[\mathbf{u}+\mathbf{v}=(u_x+v_x)\hat{\mathbf{i}}+(u_y+v_y)\hat{\mathbf{j}}+(u_z+v_z)\hat{\mathbf{k}} \nonumber\]
or subtract them to obtain:
\[\mathbf{u}-\mathbf{v}=(u_x-v_x)\hat{\mathbf{i}}+(u_y-v_y)\hat{\mathbf{j}}+(u_z-v_z)\hat{\mathbf{k}} \nonumber\]
When it comes to multiplication, we can perform the product of two vectors in two different ways. The first, which gives a scalar (a number) as the result, is called scalar product or dot product. The second, which gives a vector as a result, is called the vector (or cross) product. Both are important operations in physical chemistry.
The Scalar Product
The scalar product of vectors \(\mathbf{u}\) and \(\mathbf{v}\), also known as the dot product or inner product, is defined as (notice the dot between the symbols representing the vectors)
\[\mathbf{u}\cdot \mathbf{v}=|\mathbf{u}||\mathbf{v}|\cos \theta \nonumber\]
where \(\theta\) is the angle between the vectors. Notice that the dot product is zero if the two vectors are perpendicular to each other, and equals the product of their absolute values if they are parallel. It is easy to prove that
\[\mathbf{u}\cdot \mathbf{v}=u_xv_x+u_yv_y+u_zv_z \nonumber\]
Example \(\PageIndex{1}\)
Show that the vectors
\[ \begin{align*} \mathbf{u_1} &=\dfrac{1}{\sqrt{3}}\hat{\mathbf{i}}+\dfrac{1}{\sqrt{3}}\hat{\mathbf{j}}+\dfrac{1}{\sqrt{3}}\hat{\mathbf{k}} \\[4pt] \mathbf{u_2} &=\dfrac{1}{\sqrt{6}}\hat{\mathbf{i}}-\dfrac{2}{\sqrt{6}}\hat{\mathbf{j}}+\dfrac{1}{\sqrt{6}}\hat{\mathbf{k}} \\[4pt] \mathbf{u_3} &=-\dfrac{1}{\sqrt{2}}\hat{\mathbf{i}}+\dfrac{1}{\sqrt{2}}\hat{\mathbf{k}} \end{align*} \nonumber\]
are of unit length and are mutually perpendicular.
Solution
The length of the vectors are:
\[ \begin{align*} |\mathbf{u_1}|&=\left[\left(\dfrac{1}{\sqrt{3}}\right)^2+\left(\dfrac{1}{\sqrt{3}}\right)^2+\left(\dfrac{1}{\sqrt{3}}\right)^2\right]^{1/2}=\left[\dfrac{1}{3}+\dfrac{1}{3}+\dfrac{1}{3}\right]^{1/2}=1 \\[4pt] |\mathbf{u_2}| &=\left[\left(\dfrac{1}{\sqrt{6}}\right)^2+\left(-\dfrac{2}{\sqrt{6}}\right)^2+\left(\dfrac{1}{\sqrt{6}}\right)^2\right]^{1/2}=\left[\dfrac{1}{6}+\dfrac{4}{6}+\dfrac{1}{6}\right]^{1/2}=1 \\[4pt] |\mathbf{u_3}| &=\left[\left(-\dfrac{1}{\sqrt{2}}\right)^2+\left(\dfrac{1}{\sqrt{2}}\right)^2\right]^{1/2}=\left[\dfrac{1}{2}+\dfrac{1}{2}\right]^{1/2}=1 \end{align*} \nonumber\]
To test if two vectors are perpendicular, we perform the dot product:
\[ \begin{align*} \mathbf{u_1}\cdot \mathbf{u_2}&=\left(\dfrac{1}{\sqrt{3}}\dfrac{1}{\sqrt{6}}-\dfrac{1}{\sqrt{3}}\dfrac{2}{\sqrt{6}}+\dfrac{1}{\sqrt{3}}\dfrac{1}{\sqrt{6}}\right)=0 \\[4pt] \mathbf{u_1}\cdot \mathbf{u_3} &=\left(-\dfrac{1}{\sqrt{3}}\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{3}}\dfrac{1}{\sqrt{2}}\right)=0 \\[4pt] \mathbf{u_2}\cdot \mathbf{u_3} &=\left(-\dfrac{1}{\sqrt{6}}\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{6}}\dfrac{1}{\sqrt{2}}\right)=0 \end{align*} \nonumber\]
Therefore, we just proved that the three pairs are mutually perpendicular, and the three vectors have unit length. In other words, these vectors are the vectors \(\hat{\mathbf{i}}\), \(\hat{\mathbf{j}}\) and \(\hat{\mathbf{k}}\) rotated in space.
If the dot product of two vectors (of any dimension) is zero, we say that the two vectors are orthogonal. If the vectors have unit length, we say they are normalized. If two vectors are both normalized and they are orthogonal, we say they are orthonormal. The set of vectors shown in the previous example form an orthonormal set.[vectors:orthonormal] These concepts also apply to vectors that contain complex entries, but how do we perform the dot product in this case?
In general, the square of the modulus of a vector is
\[|\mathbf{u}|^2=\mathbf{u}\cdot \mathbf{u}=u_x^2+u_y^2+u_z^2. \nonumber\]
However, this does not work correctly for complex vectors. The square of \(i\) is -1, meaning that we risk having non-positive absolute values. To address this issue, we introduce a more general version of the dot product:
\[\mathbf{u}\cdot \mathbf{v}=u_x^*v_x+u_y^*v_y+u_z^*v_z, \nonumber\]
where the “\(*\) ” refers to the complex conjugate. Therefore, to calculate the modulus of a vector \(\mathbf{u}\) that has complex entries, we use its complex conjugate:
\[|\mathbf{u}|^2=\mathbf{u}^*\cdot \mathbf{u} \nonumber\]
Example \(\PageIndex{2}\): Calculating the Modulus of a vector
Calculate the modulus of the following vector:
\[\mathbf{u}=\hat{\mathbf{i}}+i \hat{\mathbf{j}} \nonumber\]
Solution
\[|\mathbf{u}|^2=\mathbf{u}^*\cdot \mathbf{u}=(\hat{\mathbf{i}}-i \hat{\mathbf{j}})(\hat{\mathbf{i}}+i \hat{\mathbf{j}})=(1)(1)+(-i)(i)=2\rightarrow |\mathbf{u}|=\sqrt{2} \nonumber\]
Analogously, if vectors contain complex entries, we can test whether they are orthogonal or not by checking the dot product \(\mathbf{u}^*\cdot \mathbf{v}\).
Example \(\PageIndex{3}\): Confirming orthogonality
Determine if the following pair of vectors are orthogonal (do not confuse the irrational number \(i\) with the unit vector \(\hat{\mathbf{i}}\)!)
\[\mathbf{u}=\hat{\mathbf{i}}+(1-i)\hat{\mathbf{j}} \nonumber\]
and
\[\mathbf{v}=(1+i)\hat{\mathbf{i}}+\hat{\mathbf{j}} \nonumber\]
Solution
\[\mathbf{u}^*\cdot \mathbf{v}=(\hat{\mathbf{i}}+(1+i)\hat{\mathbf{j}})((1+i)\hat{\mathbf{i}}+\hat{\mathbf{j}})=(1)(1+i)+(1+i)(1)=2+2i\neq 0 \nonumber\]
Therefore, the vectors are not orthogonal.
The Vector Product
The vector product of two vectors is a vector defined as
\[\mathbf{u}\times \mathbf{v}=|\mathbf{u}| |\mathbf{v}| \mathbf{n} \sin\theta \nonumber\]
where \(\theta\) is again the angle between the two vectors, and \(\mathbf{n}\) is the unit vector perpendicular to the plane formed by \(\mathbf{u}\) and \(\mathbf{v}\). The direction of the vector \(\mathbf{n}\) is given by the right-hand rule. Extend your right hand and point your index finger in the direction of \(\mathbf{u}\) (the vector on the left side of the \(\times\) symbol) and your forefinger in the direction of \(\mathbf{v}\). The direction of \(\mathbf{n}\), which determines the direction of \(\mathbf{u}\times \mathbf{v}\), is the direction of your thumb. If you want to revert the multiplication, and perform \(\mathbf{v}\times \mathbf{u}\), you need to point your index finger in the direction of \(\mathbf{v}\) and your forefinger in the direction of \(\mathbf{u}\) (still using the right hand!). The resulting vector will point in the opposite direction (Figure \(\PageIndex{1}\)).
The magnitude of \(\mathbf{u}\times \mathbf{v}\) is the product of the magnitudes of the individual vectors times \(\sin \theta\). This magnitude has an interesting geometrical interpretation: it is the area of the parallelogram formed by the two vectors (Figure \(\PageIndex{1}\)).
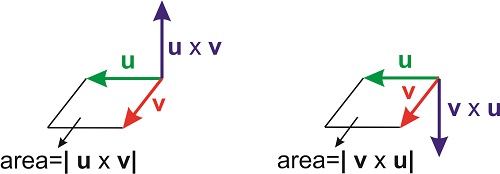
The cross product can also be expressed as a determinant:
\[\mathbf{u}\times \mathbf{v}= \begin{vmatrix} \hat{\mathbf{i}}&\hat{\mathbf{j}}&\hat{\mathbf{k}}\\ u_x&u_y&u_z\\ v_x&v_y&v_z\\ \end{vmatrix} \nonumber\]
Example \(\PageIndex{1}\):
Given \(\mathbf{u}=-2 \hat{\mathbf{i}}+\hat{\mathbf{j}}+\hat{\mathbf{k}}\) and \(\mathbf{v}=3 \hat{\mathbf{i}}-\hat{\mathbf{j}}+\hat{\mathbf{k}}\), calculate \(\mathbf{w}=\mathbf{u}\times \mathbf{v}\) and verify that the result is perpendicular to both \(\mathbf{u}\) and \(\mathbf{v}\).
Solution
\[ \begin{align*} \mathbf{u}\times \mathbf{v} &= \begin{vmatrix} \hat{\mathbf{i}}&\hat{\mathbf{j}}&\hat{\mathbf{k}}\\ u_x&u_y&u_z\\ v_x&v_y&v_z\\ \end{vmatrix}=\begin{vmatrix} \hat{\mathbf{i}}&\hat{\mathbf{j}}&\hat{\mathbf{k}}\\ -2&1&1\\ 3&-1&1\\ \end{vmatrix} \\[4pt] &=\hat{\mathbf{i}}(1+1)-\hat{\mathbf{j}}(-2-3)+\hat{\mathbf{k}}(2-3) \\[4pt] &=\displaystyle{\color{Maroon}2 \hat{\mathbf{i}}+5 \hat{\mathbf{j}}-\hat{\mathbf{k}}} \end{align*} \nonumber\]
To verify that two vectors are perpendicular we perform the dot product:
\[\mathbf{u} \cdot \mathbf{w}=(-2)(2)+(1)(5)+(1)(-1)=0 \nonumber\]
\[\mathbf{v} \cdot \mathbf{w}=(3)(2)+(-1)(5)+(1)(-1)=0 \nonumber\]
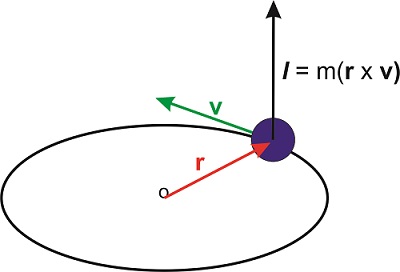
An important application of the cross product involves the definition of the angular momentum. If a particle with mass \(m\) moves a velocity \(\mathbf{v}\) (a vector), its (linear) momentum is \(\mathbf{p}=m\mathbf{v}\). Let \(\mathbf{r}\) be the position of the particle (another vector), then the angular momentum of the particle is defined as
\[\mathbf{l}=\mathbf{r}\times\mathbf{p} \nonumber\]
The angular momentum is therefore a vector perpendicular to both \(\mathbf{r}\) and \(\mathbf{p}\). Because the position of the particle needs to be defined with respect to a particular origin, this origin needs to be specified when defining the angular momentum.
Vector Normalization
A vector of any given length can be divided by its modulus to create a unit vector (i.e. a vector of unit length). We will see applications of unit (or normalized) vectors in the next chapter.
For example, the vector
\[\mathbf{u}=\hat{\mathbf{i}}+\hat{\mathbf{j}}+i\hat{\mathbf{k}} \nonumber\]
has a magnitude:
\[|\mathbf{u}|^2=1^2+1^2+(-i)(i)=3\rightarrow |\mathbf{u}|=\sqrt{3} \nonumber\]
Therefore, to normalize this vector we divide all the components by its length:
\[\hat{\mathbf{u}}=\frac{1}{\sqrt{3}}\hat{\mathbf{i}}+\frac{1}{\sqrt{3}}\hat{\mathbf{j}}+\frac{i}{\sqrt{3}}\hat{\mathbf{k}} \nonumber\]
Notice that we use the “hat” to indicate that the vector has unit length.
Need help? The links below contain solved examples.
Operations with vectors: http://tinyurl.com/mw4qmz8
External links:
- The dot product: http://patrickjmt.com/vectors-the-dot-product/
- The cross product: http://patrickjmt.com/the-cross-product/
- The dot and cross product: http://www.youtube.com/watch?v=enr7JqvehJs

