Solutions 19
- Page ID
- 47404
S19.1
\(CO_2\) is experimentally determined to be diamagnetic. If a student proposed the following structure to explain. Is a valid Lewis diagram? Does this Lewis diagram predict a diamagnetic species and if not, why?
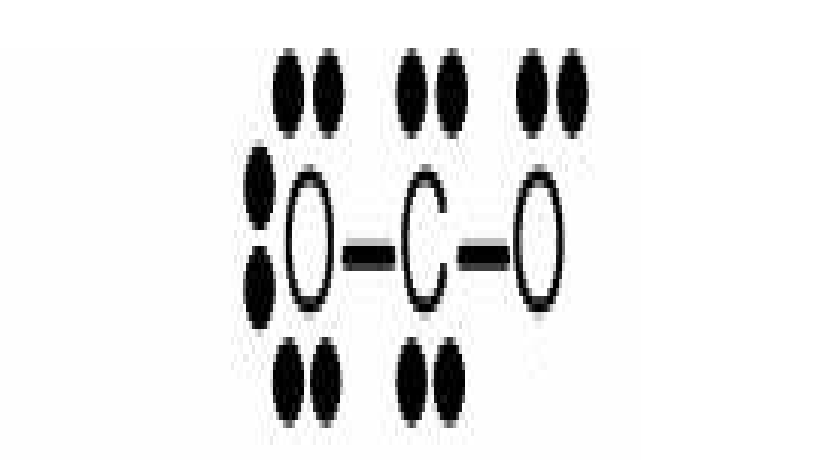
This is not a correct Lewis structure. The formal charge is not minimized, the right oxygen does not have a full octet, and the carbon is only making two bonds. However, this Lewis structure does predict a diamagnetic species since all the electrons are paired off.
S19.2
Does \(\ce{Br_2C=CHBr}\) have a dipole moment?
Yes. Because the molecule is asymmetrical, the molecule will have a net dipole moment.
S19.3
What is the value of \(\psi^2_g\) (The probability density of finding the electron) at either nucleus in \(Li^+_2\) using the below equation for \(\psi_g\) ? What is the value of \(\psi^2_g\) at the midpoint of the bond? Use \(R_e =106\; pm \) and \(S = 0.86\)
\[\psi_g = \dfrac{1}{\sqrt{2(1+S)}}(1s_a + 1s_b) \]
The hydrogenic radial function of a 1s orbital is
\[R_{1,0} (r) = 2 \left(\dfrac{Z}{a_o}\right)^{3/2} e^{-\frac{Zr}{a_o}} \]
with the angular wave function (in this case \(Y_{0,0}\))
\[Y_{0,0} = \dfrac{1}{\sqrt{4\pi}} \]
A. First we have to figure out what \(1s_a\) and \(1s_b\) are. These are the 1s orbitals of hydrogen, or the hydrogenic radial functions. The difference between a and b is which of the Li molecules is being referred to but it should not matter in this case. The hydrogenic radial function of a 1s orbital is
\[R_{1,0} (r) = 2 \left(\dfrac{Z}{a_o}\right)^{3/2} e^{-\frac{Zr}{a_o}} \]
That, multiplied with the angular wave function (in this case \(Y_{0,0}\)) gives us the equation of the 1s orbitals of hydrogen.
\[Y_{0,0} = \dfrac{1}{\sqrt{4\pi}} \]
\[R_{1,0}(r) * Y_{0,0} = (2 \left(\dfrac{3}{a_o}\right)^{3/2} e^{-\frac{3r}{a_o}})(\dfrac{1}{\sqrt{4\pi}}) \]
Here we have \(R_e=106 \; pm\), convert to meters \(R_e=106 \times 10^{-12}\). Z is the atomic number of the element, in this case \(Z=3\) for Lithium. \(a_o\) is the Bohr radius and is a constant.
\[\psi_g = \dfrac{1}{\sqrt{2(1+S)}}(2(2 \left(\dfrac{3}{a_o} \right)^{3/2} \times e^{-\dfrac{(318 \times 10^{-12})}{a_o}}\dfrac{1}{\sqrt{4\pi}})) \]
plug in \(S= 0.86\) into the equation
\[\psi_g = \dfrac{1}{\sqrt{2(1+.86)}}(2( 2 \left(\dfrac{3}{a_o}\right)^{3/2} \times e^{-\dfrac{(318 \times 10^{-12})}{a_o}})\dfrac{1}{\sqrt{4\pi}}) \]
Square \(\psi_g\) to get your final answer
\[\psi^2_g = (\dfrac{1}{\sqrt{3.72}}( 4 \left(\dfrac{3}{a_o}\right)^{3/2} \times e^{-\dfrac{(318 \times 10^{-12})}{a_o}})\dfrac{1}{\sqrt{4\pi}}))^2 \]
\[\psi^2_g = \dfrac{9.24}{a_o^2} \times e^{-\dfrac{636 \times 10^{-12}}{a_o}} \]
B. For the midpoint, use \(R_e=53\; pm \)
\[\psi^2_g = (\dfrac{1}{\sqrt{3.72}}(4(\dfrac{3}{a_o})^{3/2} \times e^{-\dfrac{(159 \times 10^{-12})}{a_o}})\dfrac{1}{\sqrt{4\pi}}))^2 \]
\[\psi^2_g = \dfrac{9.24}{a_o^2} \times e^{-\dfrac{318 \times 10^{-12}}{a_o}} \]
S19.4
The first excited states of \(H_2^-\) are formed by exciting an electron from the antibonding \(1\sigma_u\) molecular orbital to the bonding \(2\sigma_g\) orbital. Write the electron configuration of the ground state and excited-state \(H_2^-\) molecules. What is the bond order of \(H_2^-\) in both states? Is \(H_2^-\) diamagnetic or paramagentic in either state?
\(H_2^-\) is a three electron system with the electron configuration for the first excited state is \( (1\sigma_{1s})^2 (2\sigma_{1s})^1 \). The bond order is \(\dfrac{3}{2}\). The ground state electron configuration for \(H_2^-\) is \( (1\sigma_{1s})^2 (1\sigma_{1s}^*)^1 \). The bond order is \(\frac{1}{2}\). In both states there is an unpaired electron so the ion is paramagnetic.
S19.5
Which two second row homonuclear diatomic molecules do not follow conventional Molecular Orbital energy levels of the other second row homonuclear diatomic? Which are they and what is the difference?
Both \(O_2\) and \(F_2\) have molecular orbital diagrams that do not follow to others in the row with the 2p \(\sigma\) and \(\pi\) bonding orbitals switched in terms of which is lower in energy.
S19.6
A excited state of \(O_2^*\) is formed by exciting a single electron in \(O_2\) from the molecular orbital \(1\pi_g\) to the orbital \(3\sigma_u\). Note that \(^*\) is used to represent an excited state species, not an antibonding molecular orbital.
- Write the electron configuration.
- What is the bond order of \(O_2^*\)?
(a)
Ground state electron configuration for \(O_2\):
$$(1\sigma_g)^2(1\sigma_u)^2(2\sigma_g)^2(2\sigma_u)^2(1\pi_u)^4(3\sigma_g)^2(1\pi_g)^2\]
Therefore, the electron configuration for \(O_2^*\):
$$(1\sigma_g)^2(1\sigma_u)^2(2\sigma_g)^2(2\sigma_u)^2(1\pi_u)^4(3\sigma_g)^2(1\pi_g)^1(3\sigma_u)^1\]
b
$$\mbox{Bond Order}=\dfrac{\mbox{# of electrons in bonding MO - # of electrons in antibonding MO}}{2}\]
Bonding MO:
$$(2\sigma_g)^2(1\pi_u)^4(3\sigma_g)^2\]
Antibonding MO: $$(2\sigma_u)^2(1\pi_g)^1(3\sigma_u)^1\]
$$\mbox{Bond Order}=\dfrac{8-4}{2}=2\]

