Homework 15 (Due 5/13/2016)
- Page ID
- 47395
Name: ______________________________
Section: _____________________________
Student ID#:__________________________
Q15.1
What are the allowed values for each of the four quantum numbers for a hydrogen atom: n, l, ml, and ms?
Q15.2
Find the energy and wavefunction for a single electron located in one (you pick one) of the 2p orbitals of the hydrogen atom. Include all possible wavefunctions. How is the energy difference from the electron in the 2s orbital?
Q15.3
How much energy (in eV) is required to remove an electron from each of the following orbitals in a hydrogen atom (hint: The removal of an electron from a hydrogen atom is akin to moving an electron from energy state n to a n=infinity):
- 2p
- 4d
- 5s
- 6p
Q15.4
Calculate the ground-state ionization potentials for \(Li^{2+}\) and \(Be^{3+}\).
Q15.5
Calculate the wavelength of the emitted light in result of the electron's transition from 3s to 2p for \(C^{+5}\).
Q15.6
Write the equation that you need to solve to calculate the probability of a 1s hydrogen electron being found within distance \(2a_0\) nucleus. You do not need to solve, but wouldn't be a bad idea.
Q15.7
Consider the orbitals shown here in outline.
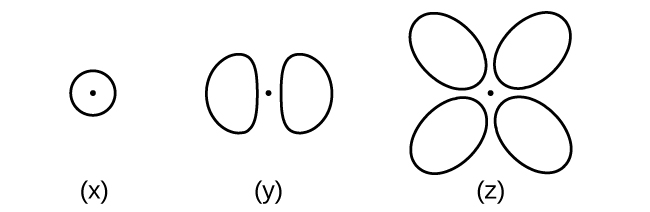
- What is the maximum number of electrons contained in an orbital of type (x)? Of type (y)? Of type (z)?
- How many orbitals of type (x) are found in a shell with n = 2? How many of type (y)? How many of type (z)?
- Write a set of quantum numbers for an electron in an orbital of type (x) in a shell with n = 4. Of an orbital of type (y) in a shell with n = 2. Of an orbital of type (z) in a shell with n = 3.
- What is the smallest possible n value for an orbital of type (x)? Of type (y)? Of type (z)?
- What are the possible l and ml values for an orbital of type (x)? Of type (y)? Of type (z)?

