Solutions 9
- Page ID
- 47384
Q9.1
Which of the following assumptions are made in Michaelis-Menten kinetics?
Q9.2
What is \(V_{max}\)?
Q9.3
What is \(K_m\)?
Q9.4
How would the ten-fold decrease in enzyme concentration affect the observed \(K_m\)?
Q9.5
You have isolated the enzyme larsenase from the rare parasite (Facultium ignorantus). This enzyme cleaves the first two numbers off of four digit dates. You flex your skills as an enzymologist and come up with the following graph of initial velocity as a function of substrate concentration:

a) From the graph, estimate \(K_m\).
b) What is the approximate value of \(V_{max}\)?
c) Is larsenase an allosteric enzyme? Explain.
Q9.6
A specific enzyme-catalyzed reaction, \(V_{max} = 0.2 \; mol/sec\) and \(K_m = 5 \;mM\). Assume the enzyme shows standard Michaelis-Menten kinetics.
- What is the rate of the reaction when \([ S ] = 10\; mM\) ?\
\[V_{max} = .2 mol/s = 200 mmol/s\]
\[K_m = 5 mM\]
\[[S] = 10 mM\]
\[V_0 = \frac{V_{max}*[S]}{K_m + [S]} = 133.333 mmol/s = .133333 mol/s\]
b. Draw a Michaelis-Menten plot of the reaction kinetics, labeling the axes and giving values for the point where you can determine \(K_m\).
Q9.7
The following data were obtained for an enzyme in the absence of an inhibitor and in the presence of an inhibitor.
| \([S] \; (mm)\) | \(V_o \; \text{(Experiment one)}\) | \(V_o \; \text{(Experiment two)}\) |
| 1 | 8.6 | 24 |
| 2 | 16 | 40 |
| 4 | 28 | 58 |
| 10 | 42 | 70 |
Draw a Lineweaver-Burke plot of the reaction kinetics, labeling the axes and giving values for the two points where each line crosses the axes.
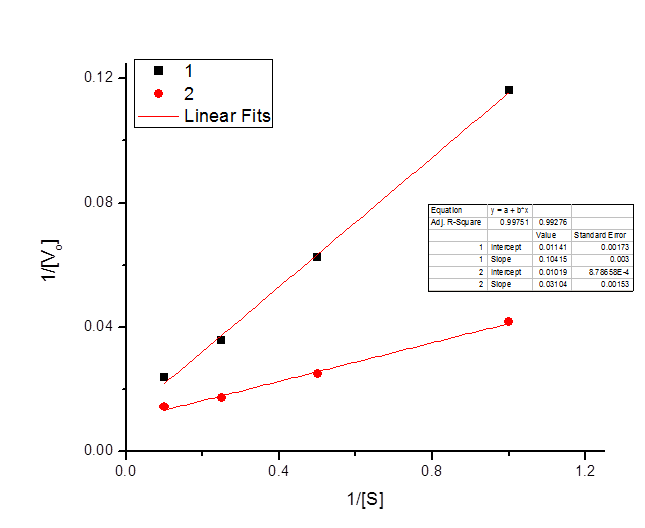
\[x_1 intercept = -\frac{.01019}{.03104} = -.3279\]
\[x_2 intercept = -\frac{.01141}{.10415} = -.1095\]
Q9.8
What is the chemical basis of enzyme specificity?
The chemical basis of enzyme specificity is the nature and design of the enzyme active site.

