Midterm 1 Solutions
- Page ID
- 48411
Problem 1
a) For each reaction mechanism, there is a corresponding rate law for that reaction and for each rate law there is a corresponding mechanism.
False
b) The half-life of first order reactions is independent from the initial concentration.
True
c) An intermediate population increases the rate of the reaction by increasing the rate constant of the reaction.
False
d) Temperature plays no significant role in determining a molecule's average kinetic energy.
False
e) The pre-exponential constant in the Arrhenius equation is a measure for the probability of a collision that occurs with sufficient energy and orientation to result in product formation.
False
f) A simple definition for the order of a reaction is that it is the number of reactant species involved in the reaction.
False
g) The potential energy surface for a reaction can be used to identify and quantify the transition state for that reaction.
True
h) Classical mechanics is a powerful theory to describe the emission of light from excited hydrogen atoms
False
i) The steric facor for an elementary reaction reduces the effective molecularity of that reaction.
False
j) Graham's law of effusion was derived from the assumption that the average speed of a gas particle is independent of its molecular mass.
False
Problem 2a
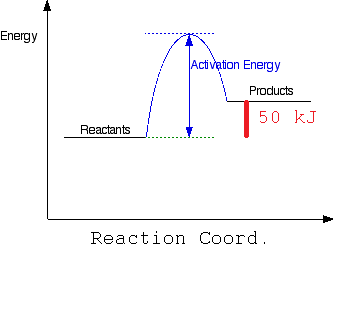
a) Draw a simple energy profile for an exothermic reaction in which 100kJ/mol is evolved, and which has an activation energy of 50 kJ/mol.

Where the activation energy is 50 kJ/mol
b) Draw a simple energy profile for an endothermic reaction in which 50 kJ/mol is absorbed and which has an activation energy of 100 kJ/mol.
Where the activation energy is 100 kJ/mol
c) Why do reaction have an activation energy and how does the exothermic or endothermic properties of the reaction affect it (if at all)?
Reactions have an activation energy because it takes energy to make and/or break the bonds of the reactants. Whether the reaction is endo or exothermic has no effect on the activation energy.
Problem 2b
Calculate the rate law for the following acid-catalyzed reaction:
\[CH_3COCH_3 + Br_2 \overset{H^+}{\longrightarrow} CH_3COCH_2Br + H^+ + Br^-\]
| Expt. # | \([CH_3COCH_3]_o\)/ M | \([Br_2]_o\) /M | \([H^+]_o\) /M | Rate of Disappearance Br2/ M*s-1 |
| 1 |
0.3 |
0.05 | 0.05 | \(5.7 \times 10^{-5}\) |
| 2 | 0.3 | 0.1 | 0.05 | \(5.7 \times 10^{-5}\) |
| 3 | 0.3 | 0.05 | 0.05 | \(1.2 \times 10^{-4}\) |
| 4 | 0.4 | 0.05 | 0.2 | \(3.1 \times 10^{-4}\) |
| 5 | 0.4 | 0.05 | 0.05 | \(7.6 \times 10^{-5}\) |
\[r = k[CH_3COCH_3]^m[H^+]^n[Br_2]^l\]
To find the values of m, n, and l two equations that keep two of the concentrations constant and vary the third must be divided by each other. To get m we divide equation 3 by 4, for n we divide 4 by 5, and for l we divide 2 by 1. Then once we know n, m, and l we can solve for k simply by picking any of the rows and filling in the numbers. Because the rates in the chart are not correct this is as far as we can correctly go.
Problem 3
A reaction is known to exhibit first order kinetics. At 300 K the concentration of reactant is reduced to one half of its initial value after 5000 s. In contrast, at 310 K the concentration is halved after 1000 s. Use this information to calculate:
a) the rate constant for the reaction at 300 K
\[t_{1/2} = \frac{Ln2}{k} \]
\[k = \frac{Ln2}{t_{1/2}} = .693/5000s = 1.39x10^{-4} s^{-1}\]
b) the time required for the reactant concentration to red reduced to one quarter of its initial value at 310 K.
Since it takes two half-times to get to one-fourth of the original concentration
c) the activation energy of the reaction.
The rate constant at 310 K is equal to:
\[k = \frac{Ln2}{1000} = 6.93x10^{-4} s^{-1}\]
\[k_1 = Ae^{\frac{-E-a}{300R}} (1) \]
\[k_2 = Ae^{\frac{-E_a}{300R}} (2)\]
Dividing equation (1) by (2) and then taking the natural log leaves us with:
\[-1.6 = -.12x10^{-4}*E_a\]
\[E_a = 124 kJ/mol\]
Problem 4
a) Compare and contraast two discussed techniques to experimentally determine reaction order and rate constants for a generic reaction. Be as specific as possible including equations.
I will just mention the two main techniques that were mentioned in class. The first being measuring the concentration of a reactant as a function of time and graphing [A] vs t, Ln[A] vs. t, and 1/[A] vs. t, finding which of those three is linear to confirm whether the reaction is zeroth, first, or second order. Then having found the linear graph k can be found by finding the slope of the line.
The second technique is the method initial rates. Given a reaction \[A + B {\longrightarrow} C\]With a chart like the one below:
| Rate of disappearance of A | Concentration of A | Concentration of B |
| R1 | [A] | [B] |
| R2 | [2A] | [B] |
| R3 | [A] | [2B] |
The equation for this reaction is \(r = k[A]^n[B]^m\) by dividing the second row of the chart by the first row we can see how R changes when we double A but leave B the same which will give us a value for n. Then we can divide the third row by the first row to find how R changes with the doubling of B which gives us m. With n and m known we can then find k easily.
b) Calculate the mean free path between HF gas molecules at 500 K and 1 atm. The diameter of the HF molecules may be taken to be 3.50 angstroms (\(10^{-10}\)).
\[\lambda = \frac{1}{\sqrt{2}\pi*d^2\frac{N}{V}}\]
Assuming we have 1 mol of HF:
\[V = \frac{nRT}{P} = \frac{1*.0821*500K}{1 atm} = 41.05 L = .04105 m^3\]
\[N = 1 mole = 6.022x10^{23}\]
\[\lambda = 125 nm\]
Previously Professor Larsen stated that the mean free path involved the radius not the diameter, this is incorrect in the equation for lambda it should be diameter not radius. If you used radius and got an answer of 500 nm you should have lost no points.
Problem 5
A) Answer the follwoing questions regarding the Maxwell-Boltzmann distribution below for a thermalized gas at two temperatures:
a) True or false: temperature T1 is higher than temperature T2?
False
b) True of false: at lower temperatures the maximum of the graph shifts to the left?
True
c) Which axis that represents kinetic energy (Vertical, horizontal, or none)?
none
d) True or False: at lower temperatures the maximum of the graph shifts to the left?
Repeat not counted
e) True or false: the y-axis on the graph represents the number of particles with a particular velocity?
True
f) True or False: the area under each curve is the same?
True
g) True or False: both curves pass through the origin of both axes at (0,0)?
True
h) True or False: at higher temperatures the maximum of the graph is greater in height?
False
B) Consider the reaction coordinate diagram shown below for the next four questions.
a) Which one of the marked points in the diagram corresponds to a transition state?
c
b) Which one of the marked points in the diagram corresponds to a reaction intermediate?
b
c) How many elementary steps are involved in this reaction?
3
d) Which is the slow (rate determining) step in the reverse reaction (right to left) (First, second, third, fourth, or fifth)?
The rate determining step in the reverse reaction is the step from e to d.

