5.2: Valence Bond Theory
- Page ID
- 20326
Valence bond (VB) theory is one of two basic theories, along with molecular orbital (MO) theory, that were developed to use the methods of quantum mechanics to explain chemical bonding. It focuses on how the atomic orbitals of the dissociated atoms combine to give individual chemical bonds when a molecule is formed. In contrast, molecular orbital theory, which will be discussed elsewhere, predict wavefunctions that cover the entire molecule.
The simplest case to consider is the hydrogen molecule, \(H_2\). When we say that the two hydrogen nuclei share their electrons to form a covalent bond, what we mean in VB theory terms is that the two spherical 1s orbitals (the grey spheres in Figure \(\PageIndex{1}\)) overlap and contain two electrons.

How far apart are the two nuclei? If they are too far apart, their respective 1s orbitals cannot overlap, and thus no covalent bond can form - they are still just two separate hydrogen atoms. As they move closer and closer together, orbital overlap begins to occur, and a bond begins to form. This lowers the potential energy of the system, as new, attractive positive-negative electrostatic interactions become possible between the nucleus of one atom and the electron of the second (Figure \(\PageIndex{2}\)). However, something else is happening at the same time: as the atoms get closer, the repulsive positive-positive interaction between the two nuclei also begins to increase.
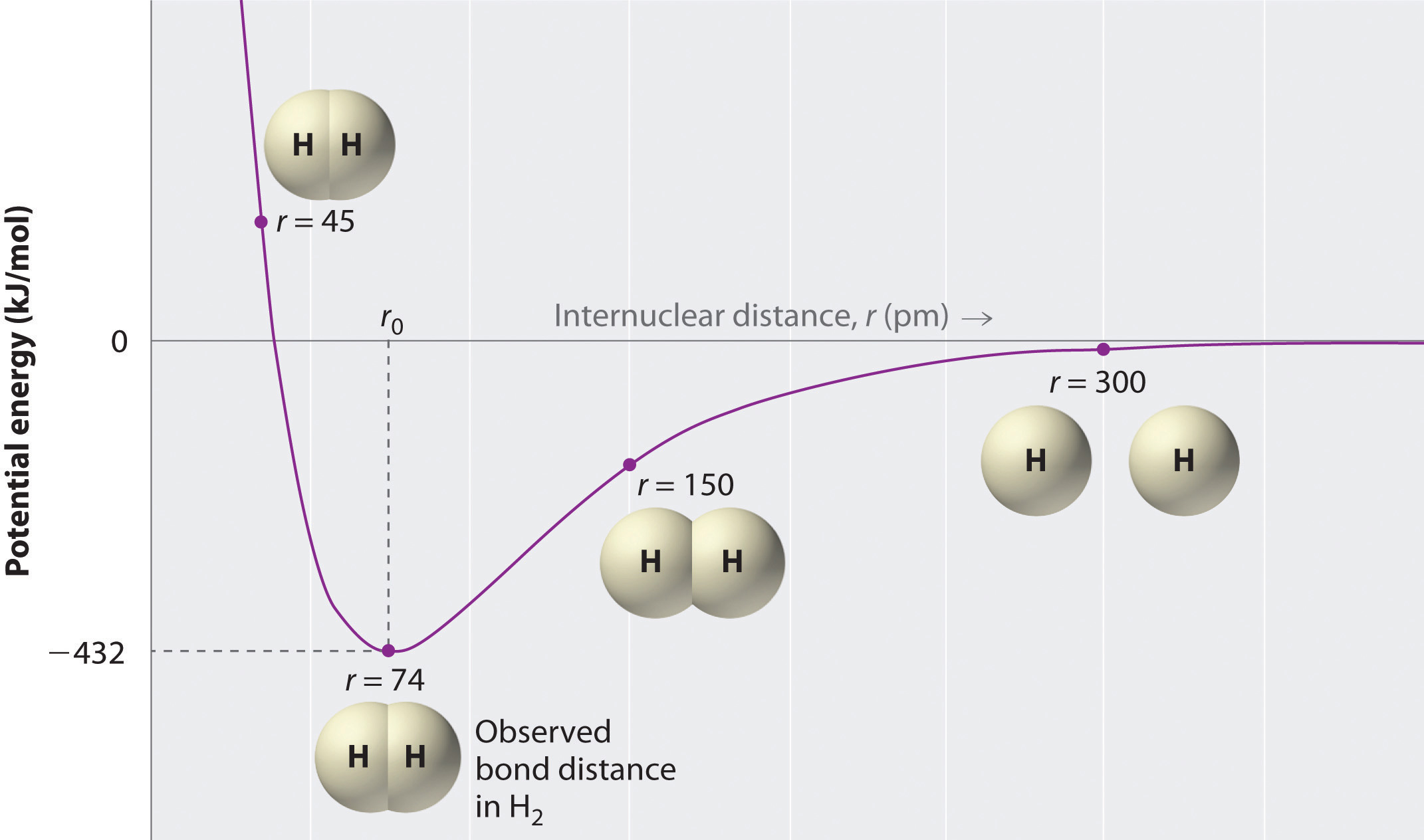
At first this repulsion is more than offset by the attraction between nuclei and electrons, but at a certain point, as the nuclei get even closer, the repulsive forces begin to overcome the attractive forces, and the potential energy of the system rises quickly. When the two nuclei are ‘too close’, we have an unstable, high-energy situation. There is a defined optimal distance between the nuclei in which the potential energy is at a minimum, meaning that the combined attractive and repulsive forces add up to the greatest overall attractive force. This optimal internuclear distance is the bond length; the distance is 74 pm for \(H_2\). Likewise, the difference in potential energy between the lowest energy state (at the optimal internuclear distance) and the state where the two atoms are completely separated is called the bond dissociation energy, or, more simply, bond strength; the \(H_2\) bond strength is 435 kJ/mol.
A comparison of some bond lengths and energies is shown in Table \(\PageIndex{1}\). We can find many of these bonds in a variety of molecules, and this table provides average values. For example, breaking the first C–H bond in CH4 requires 439.3 kJ/mol, while breaking the first C–H bond in \(\ce{H–CH2C6H5}\) (a common paint thinner) requires 375.5 kJ/mol.
| Bond | Length (pm) | Energy (kJ/mol) | Bond | Length (pm) | Energy (kJ/mol) | |
|---|---|---|---|---|---|---|
| H–H | 74 | 436 | C–O | 140.1 | 358 | |
| H–C | 106.8 | 413 | \(\mathrm{C=O}\) | 119.7 | 745 | |
| H–N | 101.5 | 391 | \(\mathrm{C≡O}\) | 113.7 | 1072 | |
| H–O | 97.5 | 467 | H–Cl | 127.5 | 431 | |
| C–C | 150.6 | 347 | H–Br | 141.4 | 366 | |
| \(\mathrm{C=C}\) | 133.5 | 614 | H–I | 160.9 | 298 | |
| \(\mathrm{C≡C}\) | 120.8 | 839 | O–O | 148 | 146 | |
| C–N | 142.1 | 305 | \(\mathrm{O=O}\) | 120.8 | 498 | |
| \(\mathrm{C=N}\) | 130.0 | 615 | F–F | 141.2 | 159 | |
| \(\mathrm{C≡N}\) | 116.1 | 891 | Cl–Cl | 198.8 | 243 |
Example \(\PageIndex{1}\): A Morse Potential Approximation
The Morse potential, named after physicist Philip M. Morse, is a convenient interatomic interaction approximation for the potential energy of a diatomic molecule.
\[V(r) = D_e \left[ 1-e^{-\beta(r-r_e)} \right]^2 \nonumber\]
Here \(r\) is the distance between the atoms, \(r_e\) is the equilibrium bond distance, \(D_e\) is the well depth (defined relative to the dissociated atoms), and \(\beta\) controls the 'width' of the potential (the smaller \(\beta\) is, the larger the well). For \(H_2\), the equilibrium bond length \(r_e = 74.1 \;pm\), the bond energy \(D_e = 7.61 \times 10^{-19} J\), and the Morse potential parameter \(\beta= 0.0193\; pm^{-1}\).
The force on the system is given by
\[F(r) = -\dfrac{dV(r)}{dr} \nonumber\]
Calculate the force for \(H_2\) and explain the status of the system (e.g., compressing, expanding, or stationary) at:
- 45 pm,
- 74 pm,
- 150 pm, and
- 500 pm.
Overlap
Valence bond theory describes a covalent bond as the overlap of half-filled atomic orbitals (each containing a single electron) that yield a pair of electrons shared between the two bonded atoms. We say that orbitals on two different atoms overlap when a portion of one orbital and a portion of a second orbital occupy the same region of space. According to valence bond theory, a covalent bond results when two conditions are met:
- an orbital on one atom overlaps an orbital on a second atom and
- the single electrons in each orbital combine to form an electron pair.
The mutual attraction between this negatively charged electron pair and the two atoms’ positively charged nuclei serves to physically link the two atoms through a force we define as a covalent bond. The strength of a covalent bond depends on the extent of overlap of the orbitals involved. Orbitals that overlap extensively form bonds that are stronger than those that have less overlap.
In addition to the distance between two orbitals, the orientation of orbitals also affects their overlap (other than for two s orbitals, which are spherically symmetric). Greater overlap is possible when orbitals are oriented such that they overlap on a direct line between the two nuclei. Figure \(\PageIndex{3}\) illustrates this for two p orbitals from different atoms; the overlap is greater when the orbitals overlap end to end rather than at an angle.
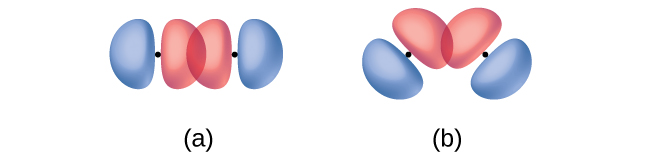
The overlap of two s orbitals (as in H2), the overlap of an s orbital and a p orbital (as in HCl), and the end-to-end overlap of two p orbitals (as in Cl2) all produce sigma bonds (σ bonds), as illustrated in Figure \(\PageIndex{4}\). A σ bond is a covalent bond in which the electron density is concentrated in the region along the internuclear axis; that is, a line between the nuclei would pass through the center of the overlap region. Single bonds in Lewis structures are described as σ bonds in valence bond theory.

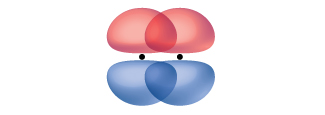
A pi bond (π bond) is a type of covalent bond that results from the side-by-side overlap of two p orbitals, as illustrated in Figure \(\PageIndex{5}\). In a π bond, the regions of orbital overlap lie on opposite sides of the internuclear axis. Along the axis itself, there is a node, that is, a plane with no probability of finding an electron.
While all single bonds are σ bonds, multiple bonds consist of both σ and π bonds. As the Lewis structures in suggest, O2 contains a double bond, and N2 contains a triple bond. The double bond consists of one σ bond and one π bond, and the triple bond consists of one σ bond and two π bonds. Between any two atoms, the first bond formed will always be a σ bond, but there can only be one σ bond in any one location. In any multiple bond, there will be one σ bond, and the remaining one or two bonds will be π bonds. These bonds are described in more detail later in this chapter.
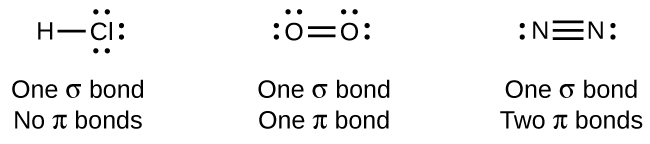
As seen in Table \(\PageIndex{2}\), an average carbon-carbon single bond is 347 kJ/mol, while in a carbon-carbon double bond, the π bond increases the bond strength by 267 kJ/mol. Adding an additional π bond causes a further increase of 225 kJ/mol. We can see a similar pattern when we compare other σ and π bonds. Thus, each individual π bond is generally weaker than a corresponding σ bond between the same two atoms. In a σ bond, there is a greater degree of orbital overlap than in a π bond.
Counting σ and π Bonds
Butadiene, C6H6, is used to make synthetic rubber. Identify the number of σ and π bonds contained in this molecule.

Butadiene
Solution
There are six σ C–H bonds and one σ C–C bond, for a total of seven from the single bonds. There are two double bonds that each have a π bond in addition to the σ bond. This gives a total nine σ and two π bonds overall.
Exercise \(\PageIndex{2}\)
Identify each illustration as depicting a σ or π bond:
- side-by-side overlap of a 4p and a 2p orbital
- end-to-end overlap of a 4p and 4p orbital
- end-to-end overlap of a 4p and a 2p orbital

- Answer
-
(a) is a \(π\) bond with a node along the axis connecting the nuclei while (b) and (c) are \(σ\) bonds that overlap along the axis.
The Valence Bond Wavefunction
In the hydrogen molecule, VB theory uses two electrons (electron 1 and electron 2) in two 1s atomic orbitals (\(\psi_a\) and \(\psi_b\)) on the hydrogen atoms(atom \(a\) and atom \(b\)). The simplest description of a \(H_2\) molecule with two electrons and two nuclei is
\[ \psi_{simple} = \psi_a(1)\psi_b(2) \label{VBA}\]
Equation \(\ref{VBA}\) means electron \(1\) is in \(\psi_a\) of atom \(a\) and electron \(2\) is in \(\psi_a\) on the atom \(b\). Where \( \psi_a\) and \( \psi_b\) may be the \(1s\) orbitals as the simplest wavefunction (\(n=1\), \(l=0\), \(m_l\)). The \(\psi_{simple}\) wavefunction predicts an energy that is about 6% of the experimental value at a bond length of 0.90 pm, which is considerably longer than the experimental value of 0.74 pm (Table \(\PageIndex{1}\)). However, Equation \(\ref{VBA}\) does not address the indistinguishability of the problem, i.e, we cannot distinguished each electron from the other.
Distinguishable vs. Indistinguishable Particles
Assume you have two particle A and B in states 1 and 2. If the two particle are distinguishable, then by exchanging the particles A and B, you will obtain a new state that will have the same properties as the old state. However, for indistinguishable particles, exchanging A and B is a transformation that does nothing and you have the same physical state. This means that for indistinguishable particles, particle labels are unphysical and they represent a redundancy in describing the physical state.
To account for the indistinguishable nature of the two electrons in the system, a covalent wavefunction that is better than Equation \(\ref{VBA}\) can be constructed (ignoring spin effect):
\[ \psi_{covalent} = \psi_a(1)\psi_b(2) + \psi_a(2)\psi_b(1) \label{VBC}\]
Equation \(\ref{VBC}\) means electron \(1\) is sometimes in \(\psi_a\) on atom \(a\) and electron \(2\) is on the atom \(b\) (left term of right hand side of Equation) and sometime electron \(1\) is sometimes in \(\psi_b\) on atom \(b\) and electron \(2\) is in \(\psi_a\) on the atom \(a\) (right term of right hand side of Equation). Notice that in contrast to Equation \(\ref{VBA}\), if the two electron labels are switched, the wavefunction in Equation \(\ref{VBC}\) does not change. The potential energy curve for the \(\psi_{covalent}\) wavefunction predicts a bond energy that is about 72% at a bond length of 0.87 pm (Table \(\PageIndex{2}\)), so the \(\psi_{covalent}\) wavefunction is more accurate than \(\psi_{simple}\).
To be more accurate within VB theory, the possibility that both electrons may be on atom a (\( \psi_a(1)\psi_a(2)\)) or on atom b (\( \psi_b(1)\psi_b(2)\)) should also be taken into account. This introduces an ionic contribution:
\[ \psi_{ionic} = \psi_a(1)\psi_a(2) + \psi_b(2)\psi_b(1) \label{VBD}\]
Notice that Equation \(\ref{VBD}\) addresses indistinguishability since the wavefunction is unchanged if the two electron labels are switched. The more complete VB wavefunction is a linear combination of both \(\psi_{covalent}\) and \(\psi_{ionic}\):
\[\psi_{AB} = Ψ_{covalent} + λ\psi_{ionic} \label{VBE}\]
where \(\lambda\) quantifies the amount of ionic character to the bond, e.g., if \(\lambda=0\), then the bond is purely covalent. The potential energy curve for the \(\psi_{AB}\) wavefunction predicts a bond energy that is ~80% of the experimental value and a reasonably accurate bond length of 0.77 pm (Table \(\PageIndex{1}\)). Additional tinkering with the wavefunction leads to even better results, but is beyond the scope of this discussion. It should be noted that the wavefunctions in Equations \(\ref{VBC}\), \(\ref{VBD}\), and \(\ref{VBE}\) are unnormalized.
| Wavefunction | Bond Energy (kJ mol-1) | Bond Length (pm) |
|---|---|---|
|
|
435 | 0.74 |
|
|
25 | 0.90 |
|
|
301 | 0.87 |
|
|
335 | 0.77 |
Two-Atom Bonds
The central gist of VB theory is that a covalent bond is formed between the two atoms by the overlap of half filled valence atomic orbitals of each atom containing one unpaired electron.
Example \(\PageIndex{3}\): Percent Ionic Character
Calculate the relative fraction of the contribution of the ionic character to the VB wavefunction. Assuming that the ionic character in \(HBr\) bond is 20%.
Solution
From Equation \(\ref{VBE}\), the percent ionic character is given by:
\[\dfrac{λ^2}{1 + λ^2} \times 100\% \nonumber\]
Therefore,
\[20 \% = 100\% \dfrac{λ^2}{1 + λ^2} \nonumber\]
\[20 \% + 20 \% λ^2 = 100 \% λ^2 \nonumber\]
\[20 \% = 100 \%λ^2 – 20λ^2 \nonumber\]
\[20 \% = 80 \%λ^2 \nonumber\]
Therefore,
\[λ^2 = \dfrac{20}{80} \nonumber\]
Hence, \(λ=\sqrt{20/80}= 0.5\) and the fraction of contribution of ionic character to \(\psi_{AB}\) is 0.5 or 50%.
Linus Pauling used the pair bonding ideas of Lewis together with Heitler–London theory to develop two key concepts in VB theory: resonance and orbital hybridization. These will be addressed in later Modules.
Summary
Valence bond theory describes bonding as a consequence of the overlap of two separate atomic orbitals on different atoms that creates a region with one pair of electrons shared between the two atoms. When the orbitals overlap along an axis containing the nuclei, they form a σ bond. When they overlap in a fashion that creates a node along this axis, they form a π bond.
Contributors and Attributions
Organic Chemistry With a Biological Emphasis by Tim Soderberg (University of Minnesota, Morris)
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).
- http://physics.stackexchange.com

