2.6: Potential Energy Surfaces
- Page ID
- 20275
A potential energy surface (PES) describes the potential energy of a system, especially a collection of atoms, in terms of certain parameters, normally the positions of the atoms. The surface might define the energy as a function of one or more coordinates; if there is only one coordinate, the surface is called a potential energy curve or energy profile. It is helpful to use the analogy of a landscape: for a system with two degrees of freedom (e.g. two bond lengths), the value of the energy (analogy: the height of the land) is a function of two bond lengths (analogy: the coordinates of the position on the ground). The Potential Energy Surface represents the concepts that each geometry (both external and internal) of the atoms of the molecules in a chemical reaction is associated with it a unique potential energy. This creates a smooth energy “landscape” and chemistry can be viewed from a topology perspective (of particles evolving over "valleys""and passes").
Potential Energy Curves (1-D Potential Energy Surfaces)
The PES is the energy of a molecule as a function of the positions of its nuclei \(r\). This energy of a system of two atoms depends on the distance between them. At large distances the energy is zero, meaning “no interaction”. At distances of several atomic diameters attractive forces dominate, whereas at very close approaches the force is repulsive, causing the energy to rise. The attractive and repulsive effects are balanced at the minimum point in the curve. Plots that illustrate this relationship are quite useful in defining certain properties of a chemical bond.
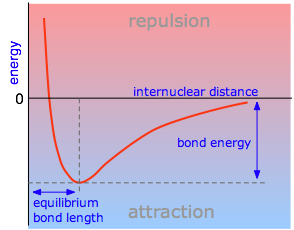
The internuclear distance at which the potential energy minimum occurs defines the bond length. This is more correctly known as the equilibrium bond length, because thermal motion causes the two atoms to vibrate about this distance. In general, the stronger the bond, the smaller will be the bond length.
Attractive forces operate between all atoms, but unless the potential energy minimum is at least of the order of RT, the two atoms will not be able to withstand the disruptive influence of thermal energy long enough to result in an identifiable molecule. Thus we can say that a chemical bond exists between the two atoms in H2. The weak attraction between argon atoms does not allow Ar2 to exist as a molecule, but it does give rise to the van Der Waals force that holds argon atoms together in its liquid and solid forms.
Potential, Kinetic, and Total Energy for a System
Potential energy and kinetic energy Quantum theory tells us that an electron in an atom possesses kinetic energy \(K\) as well as potential energy \(V\), so the total energy \(E\) is always the sum of the two: \(E = V + K\). The relation between them is surprisingly simple: \(K = –0.5 V\). This means that when a chemical bond forms (an exothermic process with \(ΔE < 0\)), the decrease in potential energy is accompanied by an increase in the kinetic energy (embodied in the momentum of the bonding electrons), but the magnitude of the latter change is only half as much, so the change in potential energy always dominates. The bond energy \(–ΔE\) has half the magnitude of the fall in potential energy.
Mathematical definition and computation
The geometry of a set of atoms can be described by a vector, r, whose elements represent the atom positions. The vector \(r\) could be the set of the Cartesian coordinates of the atoms, or could also be a set of inter-atomic distances and angles. Given \(r\), the energy as a function of the positions, \(V(r)\), is the value of \(V(r)\) for all values of \(r\) of interest. Using the landscape analogy from the introduction, \(V(r)\) gives the height on the "energy landscape" so that the concept of a potential energy surface arises. An example is the PES for water molecule (Figure \(\PageIndex{1}\)) that show the energy minimum corresponding to optimized molecular structure for water- O-H bond length of 0.0958 nm and H-O-H bond angle of 104.5°
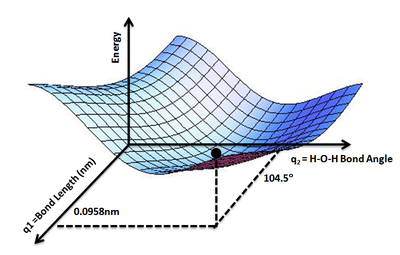
Figure \(\PageIndex{2}\): PES for water molecule: Shows the energy minimum corresponding to optimized molecular structure for water- O-H bond length of 0.0958nm and H-O-H bond angle of 104.5°. of Wikipedia (Credit: Aimnature).
The Dimensionality of a Potential Energy Surface
To define an atom’s location in 3-dimensional space requires three coordinates (e.g., \(x\), \(y\),and \(z\) or \(r\), \(\theta\) and \(phi\) in Cartesian and Spherical coordinates) or degrees of freedom. However, a reaction and hence the corresponding PESs do not depend of the absolute position of the reaction, only the relative positions (internal degrees). Hence both translation and rotation of the entire system can be removed (each with 3 degree of freedom, assuming non-linear geometries). So the dimensionality of a PES is
\[3N-6\]
where \(N\) is the number of atoms involves in the reaction, i.e., the number of atoms in each reactants). The PES is a hypersurface with many degrees of freedom and typically only a few are plotted at any one time for understanding. See Calculate Number of Vibrational Modes to get a more details picture of how this applies to calculating the number of vibrations in a molecule
To study a chemical reaction using the PES as a function of atomic positions, it is necessary to calculate the energy for every atomic arrangement of interest. Methods of calculating the energy of a particular atomic arrangement of atoms are well described in the computational chemistry article, and the emphasis here will be on finding approximations of \((V(r)\) to yield fine-grained energy-position information.
For very simple chemical systems or when simplifying approximations are made about inter-atomic interactions, it is sometimes possible to use an analytically derived expression for the energy as a function of the atomic positions. An example is
\[H + H_2 \rightarrow H_2 + H\]
system as a function of the three H-H distances. For more complicated systems, calculation of the energy of a particular arrangement of atoms is often too computationally expensive for large scale representations of the surface to be feasible.
Application of Potential Energy Surfaces
A PES is a conceptual tool for aiding the analysis of molecular geometry and chemical reaction dynamics. Once the necessary points are evaluated on a PES, the points can be classified according to the first and second derivatives of the energy with respect to position, which respectively are the gradient and the curvature. Stationary points (or points with a zero gradient) have physical meaning: energy minima correspond to physically stable chemical species and saddle points correspond to transition states, the highest energy point on the reaction coordinate (which is the lowest energy pathway connecting a chemical reactant to a chemical product). Three
- PES do not show kinetic energy, only potential energy.
- At T = 0 K (no KE), species will want to be at the lowest possible potential energy, (i.e., at a minimum on the PES).
- Between any two minima (valley bottoms) the lowest energy path will pass through a maximum at a saddle point, which we call that saddle point a transition-state structure.
The PES concept finds application in fields such as chemistry and physics, especially in the theoretical sub-branches of these subjects. It can be used to theoretically explore properties of structures composed of atoms, for example, finding the minimum energy shape of a molecule or computing the rates of a chemical reaction.
Contributors and Attributions
- Wikipedia
Stephen Lower, Professor Emeritus (Simon Fraser U.) Chem1 Virtual Textbook

