1.8: Molecular Collisions & the Mean Free Path
- Last updated
- Save as PDF
- Page ID
- 47224
Collision theory is a theory proposed independently by Max Trautz in 1916 and William Lewis in 1918, that qualitatively explains how chemical reactions occur and why reaction rates differ for different reactions. The collision theory states that when suitable particles of the reactant hit each other, only a certain percentage of the collisions cause any noticeable or significant chemical change; these successful changes are called successful collisions. The successful collisions have enough energy, also known as activation energy, at the moment of impact to break the preexisting bonds and form all new bonds. This results in the products of the reaction. Increasing the concentration of the reactant particles or raising the temperature, thus bringing about more collisions and therefore many more successful collisions, increases the rate of reaction.
Collision Energy
Consider two particles \(A\) and \(B\) in a system. The kinetic energy of these two particles is
\[K_{AB} = \dfrac{\textbf{p}_A^2}{2m_A} + \dfrac{\textbf{p}_B^2}{2m_B} \label{6}\]
Let us change to center-of-mass \(\left( \textbf{P} \right)\) and relative \(\left( \textbf{p} \right)\) momenta, which are given by
\[\textbf{P} = \textbf{p}_A + \textbf{p}_B, \: \: \: \textbf{p} = \dfrac{m_B \textbf{p}_a - m_A \textbf{p}_B}{M} \label{7}\]
where \(M = m_A + m_B\) is the total mass of the two particles. Substituting this into the kinetic energy, we find
\[K_{AB} = \dfrac{\textbf{p}_A^2}{2m_A} + \dfrac{\textbf{p}_B^2}{2m_B} = \dfrac{\textbf{P}^2}{2M} + \dfrac{\textbf{p}^2}{2 \mu} \label{8}\]
where
\[\mu = \dfrac{m_A m_B}{M} \label{9}\]
is called the reduced mass of the two particles. Note that the kinetic energy separates into a sum of a center-of-mass term and a relative term.
Now the relative position is \(\textbf{r} = \textbf{r}_A - \textbf{r}_B\) so that the relative velocity is \(\dot{\textbf{r}} = \dot{\textbf{r}}_A - \dot{\textbf{r}}_B\) or \(\textbf{v} = \textbf{v}_A - \textbf{v}_B\). Thus, if the two particles are approaching each other such that \(\textbf{v}_A = - \textbf{v}_B\), then \(\textbf{v} = 2 \textbf{v}_A\). However, by equipartitioning the relative kinetic energy, being mass independent, is
\[\left< \dfrac{\textbf{p}^2}{2 \mu} \right> = \dfrac{3}{2} k_B T \label{10}\]
which is called the collision energy.
Collision cross section
Consider two molecules in a system. The probability that they will collide increases with the effective “size” of each particle. However, the size measure that is relevant is the apparent cross-section area of each particle. For simplicity, suppose the particles are spherical, which is not a bad approximation for small molecules. If we are looking at a sphere, what we perceive as the size of the sphere is the cross section area of a great circle. Recall that each spherical particle has an associated “collision sphere” that just encloses two particles at closest contact, i.e., at the moment of a collision, and that this sphere is a radius \(d\), where \(d\) is the diameter of each spherical particle (see lecture 5). The cross-section of this collision sphere represents an effective cross section for each particle inside which a collision is imminent. The cross-section of the collision sphere is the area of a great circle, which is \(\pi d^2\). We denote this apparent cross section area \(\sigma\). Thus, for spherical particles \(A\) and \(B\) with diameters \(d_A\) and \(d_B\), the individual cross sections are
\[\sigma_A = \pi d_A^2, \: \: \: \sigma_B = \pi d_B^2 \label{11}\]
The collision cross section, \(\sigma_{AB}\) is determined by an effective diameter \(d_{AB}\) characteristic of both particles. The collision probability increases of both particles have large diameters and decreases if one of them has a smaller diameter than the other. Hence, a simple measure sensitive to this is the arithmetic average
\[d_{AB} = \dfrac{1}{2} \left( d_A + d_B \right) \label{12}\]
and the resulting collision cross section becomes
\[\begin{align} \sigma_{AB} &= \pi d_{AB}^2 \\ &= \pi \left( \dfrac{d_A + d_B}{2} \right)^2 \\ &= \dfrac{\pi}{4} \left( d_A^2 + 2d_A d_B + d_B^2 \right) \\ &= \dfrac{1}{4} \left( \sigma_A + 2 \sqrt{\sigma_A \sigma_B} + \sigma_B \right) \\ &= \dfrac{1}{2} \left[ \left( \dfrac{\sigma_A + \sigma_B}{2} \right) + \sqrt{\sigma_A \sigma_B} \right] \end{align} \label{13}\]
which, interestingly, is an average of the two types of averages of the two individual cross sections, the arithmetic and geometric averages!
Average collision Frequency
Consider a system of particles with individual cross sections \(\sigma\). A particle of cross section \(\sigma\) that moves a distance \(l\) in a time \(\Delta t\) will sweep out a cylindrical volume (ignoring the spherical caps) of volume \(\sigma l\) (Figure \(\PageIndex{1}\)). If the system has a number density \(\rho\), then the number of collisions that will occur is
\[N_{\text{coll}} = \rho \sigma l \label{14}\]
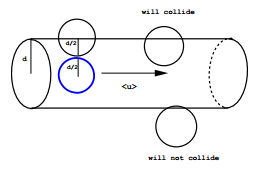
We define the average collision rate as \(N_{\text{coll}}/ \Delta t\), i.e.,
\[\gamma = \dfrac{N_{\text{coll}}}{\Delta t} = \dfrac{\rho \sigma l}{\Delta t} = \rho \sigma \langle | \textbf{v} | \rangle \label{15}\]
where \(\langle | \textbf{v} | \rangle\) is the average relative speed. If all of the particles are of the same type (say, type \(A\)), then performing the average over a Maxwell-Boltzmann speed distribution gives
\[\langle | \textbf{v} | \rangle = \sqrt{\dfrac{8 k_B T}{\pi \mu}} \label{16}\]
where \(\mu = m_A/2\) is the reduced mass. The average speed of a particle is
\[\langle | \textbf{v}_A | \rangle = \sqrt{\dfrac{8 k_B T}{\pi m_A}} \label{17}\]
so that
\[\langle | \textbf{v} | \rangle = \sqrt{2} \langle | \textbf{v}_A | \rangle \label{18}\]
Mean Free Path
The mean free path is defined as the distance a particle will travel, on average, before experiencing a collision event. This is defined as the product of the speed of a particle and the time between collisions. The former is \(\langle | \textbf{v} | \rangle/ \sqrt{2}\), while the latter is \(1/\gamma\). Hence, we have
\[\lambda = \dfrac{\langle | \textbf{v} |\rangle}{\sqrt{2} \rho \sigma \langle | \textbf{v} | \rangle} = \dfrac{1}{\sqrt{2} \rho \sigma} \label{19}\]
Random Walks
In any system, a particle undergoing frequent collisions will have the direction of its motion changed with each collision and will trace out a path that appears to be random. In fact, if we treat the process as statistical, then, we are, in fact, treating each collision event as a random event, and the particle will change its direction at random times in random ways! Such a path might appear as shown in Figure \(\PageIndex{2. Such a path is often referred to as a random walk path.
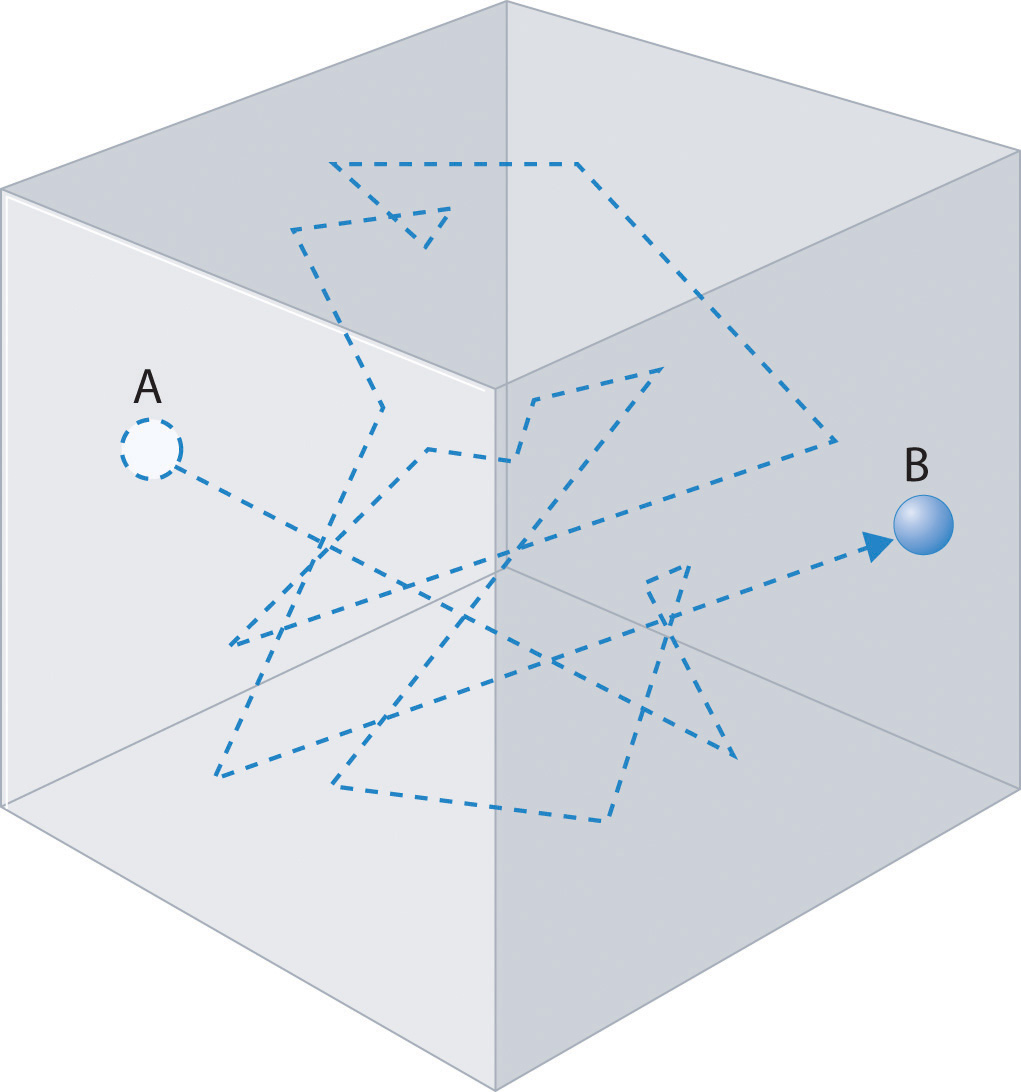
In order to analyze such paths, let us consider a random walk in one dimension. We’ll assume that the particle move a mean-free path length \(\lambda\) between collisions and that each collision changes the direction of the particles motion, which in one dimension, means that the particle moves either to the right or to the left after each event. This can be mapped onto a metaphoric “coin toss” that can come up heads “H” or tails “T”, with “H” causing motion to the right, and “T” causing motion to the left.
In three dimensions, we consider the three spatial directions to be independent, hence, the probability distribution for a particle to diffuse to a location \(\textbf{r} = (x, y, z)\) is just a product of the three one-dimensional distributions:
\[\mathcal{P}(\textbf{r}) = P(x) \: P(y) \: P(z) = \dfrac{1}{(4 \pi D t) ^{3/2}} \: e^{-\left( x^2 + y^2 + z^2 \right)/4Dt} \label{35}\]
where \(D\) is the diffusion constant. If we are only interested in diffusion over a distance \(r\), we can introduce spherical coordinates, integrate over the angles, and we find that
\[P(r, t) = \dfrac{4 \pi}{(4 \pi D t)^{3/2}} \: E^{-r^2/4Dt} \label{36}\]
Rates of Diffusion or Effusion
Graham’s law is an empirical relationship that states that the ratio of the rates of diffusion or effusion of two gases is the square root of the inverse ratio of their molar masses. The relationship is based on the postulate that all gases at the same temperature have the same average kinetic energy. We can write the expression for the average kinetic energy of two gases with different molar masses:
\[KE=\dfrac{1}{2}\dfrac{M_{\rm A}}{N_A}v_{\rm rms,A}^2=\dfrac{1}{2}\dfrac{M_{\rm B}}{N_A}v_{\rm rms,B}^2\label{6.8.2}\]
Multiplying both sides by 2 and rearranging give
\[\dfrac{v_{\rm rms, B}^2}{v_{\rm rms,A}^2}=\dfrac{M_{\rm A}}{M_{\rm B}}\label{6.8.3}\]
Taking the square root of both sides gives
\[\dfrac{v_{\rm rms, B}}{v_{\rm rms,A}}=\sqrt{\dfrac{M_{\rm A}}{M_{\rm B}}}\label{6.8.4}\]
Thus the rate at which a molecule, or a mole of molecules, diffuses or effuses is directly related to the speed at which it moves. Equation \(\ref{6.8.4}\) shows that Graham’s law is a direct consequence of the fact that gaseous molecules at the same temperature have the same average kinetic energy.
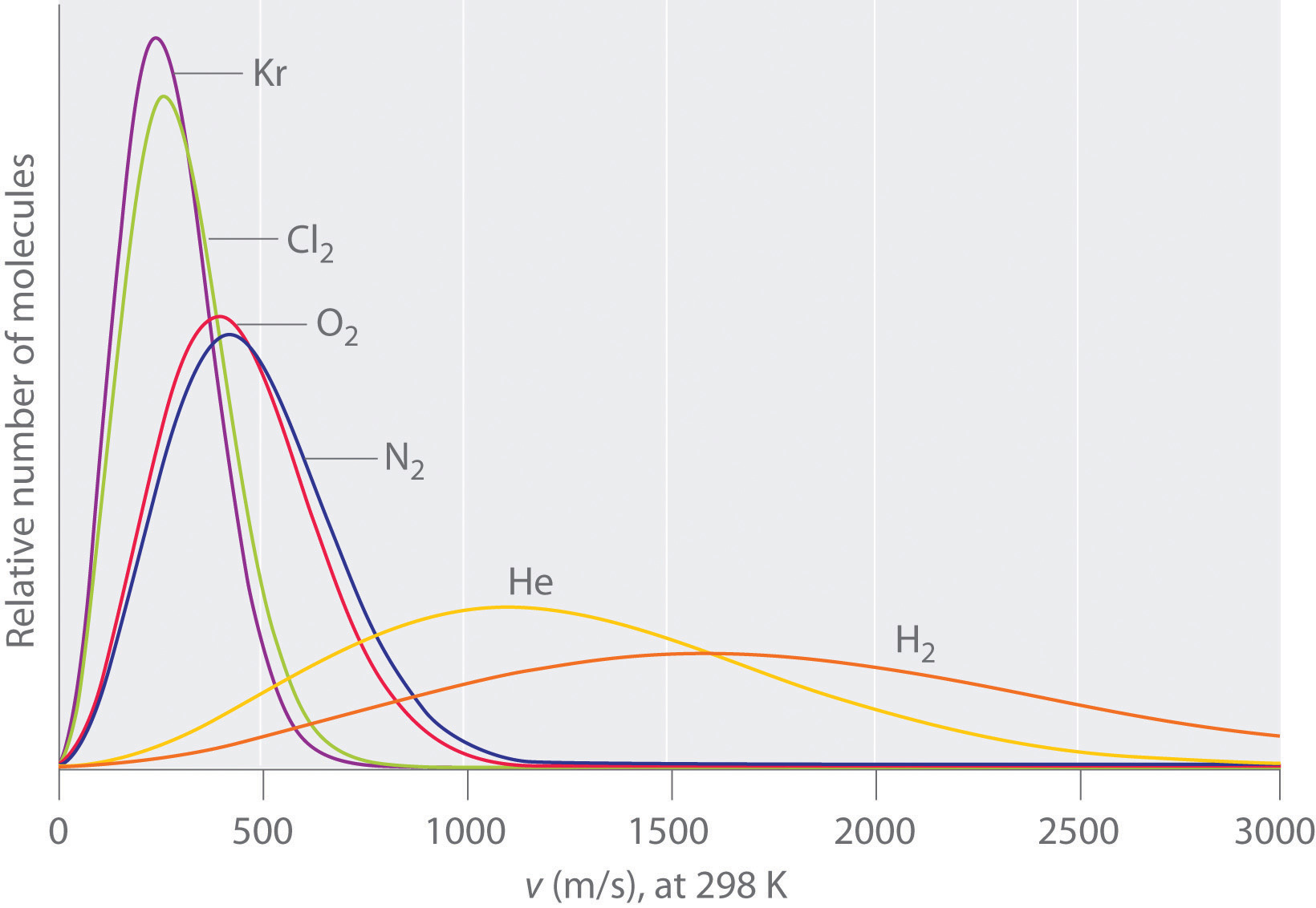
The lightest gases have a wider distribution of speeds and the highest average speeds.
Molecules with lower masses have a wider distribution of speeds and a higher average speed.
Gas molecules do not diffuse nearly as rapidly as their very high speeds might suggest. If molecules actually moved through a room at hundreds of miles per hour, we would detect odors faster than we hear sound. Instead, it can take several minutes for us to detect an aroma because molecules are traveling in a medium with other gas molecules. Because gas molecules collide as often as 1010 times per second, changing direction and speed with each collision, they do not diffuse across a room in a straight line.
The denser the gas, the shorter the mean free path.
Example \(\PageIndex{2}\)
Calculate the rms speed of a sample of cis-2-butene (C4H8) at 20°C.
Given: compound and temperature
Asked for: rms speed
Strategy:
Calculate the molar mass of cis-2-butene. Be certain that all quantities are expressed in the appropriate units and then use Equation \(\ref{6.8.5}\) to calculate the rms speed of the gas.
Solution:
To use Equation \(\ref{6.8.4}\), we need to calculate the molar mass of cis-2-butene and make sure that each quantity is expressed in the appropriate units. Butene is C4H8, so its molar mass is 56.11 g/mol. Thus
\[u_{\rm rms}=\sqrt{\dfrac{3RT}{M}}=\rm\sqrt{\dfrac{3\times8.3145\;\dfrac{J}{K\cdot mol}\times(20+273)\;K}{56.11\times10^{-3}\;kg}}=361\;m/s\]
or approximately 810 mi/h.Exercise \(\PageIndex{2}\)
Calculate the rms speed of a sample of radon gas at 23°C.
Answer: 1.82 × 102 m/s (about 410 mi/h)
Contributors and Attributions
- Wikipedia

