1.4: Real Gases
- Page ID
- 47220
According to Boyle's law, the product PV is a constant at any given temperature, so a plot of PV as a function of the pressure of an ideal gas yields a horizontal straight line. This implies that any increase in the pressure of the gas is exactly counteracted by a decrease in the volume as the molecules are crowded closer together. But we know that the molecules themselves are finite objects having volumes of their own, and this must place a lower limit on the volume into which they can be squeezed. So we must reformulate the ideal gas equation of state as a relation that is true only in the limiting case of zero pressure:
\[\lim_{P \rightarrow 0} PV=nRT\]
So what happens when a real gas is subjected to a very high pressure? The outcome varies with both the molar mass of the gas and its temperature, but in general we can see the the effects of both repulsive and attractive intermolecular forces:
- Repulsive forces: As a gas is compressed, the individual molecules begin to get in each other's way, giving rise to a very strong repulsive force acts to oppose any further volume decrease. We would therefore expect the PV vs P line to curve upward at high pressures, a nd this is in fact what is observed for all gases at sufficiently high pressures.
- Attractive forces: At very close distances, all molecules repel each other as their electron clouds come into contact. At greater distances, however, brief statistical fluctuations in the distribution these electron clouds give rise to a universal attractive force between all molecules. The more electrons in the molecule (and thus the greater the molecular weight), the greater is this attractive force. As long as the energy of thermal motion dominates this attractive force, the substance remains in the gaseous state, but at sufficiently low temperatures the attractions dominate and the substance condenses to a liquid or solid.
The universal attractive force described above is known as the dispersion, or London force. There may also be additional (and usually stronger) attractive forces related to charge imbalance in the molecule or to hydrogen bonding. These various attractive forces are often referred to collectively as van der Waals forces. A plot of PV/RT as a function of pressure is a very sensitive indicator of deviations from ideal behavior, since such a plot is just a horizontal line for an ideal gas. The two illustrations below show how these plots vary with the nature of the gas, and with temperature.
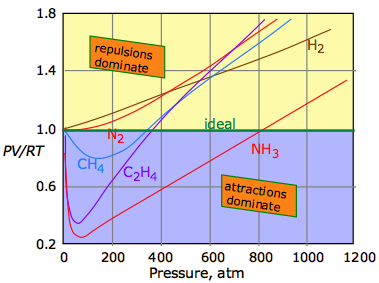
Intermolecular attractions, which generally increase with molecular weight, cause the PV product to decrease as higher pressures bring the molecules closer together and thus within the range of these attractive forces; the effect is to cause the volume to decrease more rapidly than it otherwise would. The repulsive forces always eventually win out. But as the molecules begin to intrude on each others' territory, the stronger repulsive forces cause the curve to bend upward.
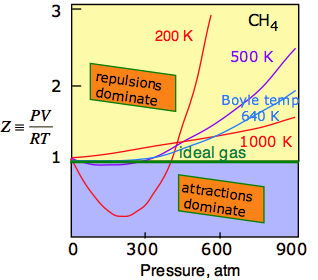
The temperature makes a big difference! At higher temperatures, increased thermal motions overcome the effects of intermolecular attractions which normally dominate at lower pressures. So all gases behave more ideally at higher temperatures. For any gas, there is a special temperature (the Boyle temperature) at which attractive and repulsive forces exactly balance each other at zero pressure. As you can see in this plot for methane, this some of this balance does remain as the pressure is increased.
The van der Waals Equation of State
How might we modify the ideal gas equation of state to take into account the effects of intermolecular interactions? The first and most well known answer to this question was offered by the Dutch scientist J.D. van der Waals (1837-1923) in 1873. The ideal gas model assumes that the gas molecules are merely points that occupy no volume; the "V" term in the equation is the volume of the container and is independent of the nature of the gas.

van der Waals recognized that the molecules themselves take up space that subtracts from the volume of the container, so that the “volume of the gas” V in the ideal gas equation should be replaced by the term (V–b), in which b relates to the excluded volume, typically of the order of 20-100 cm3 mol–1. The excluded volume surrounding any molecule defines the closest possible approach of any two molecules during collision. Note that the excluded volume is greater then the volume of the molecule, its radius being half again as great as that of a spherical molecule.
The other effect that van der Waals needed to correct for are the intermolecular attractive forces. These are ignored in the ideal gas model, but in real gases they exert a small cohesive force between the molecules, thus helping to hold the gas together and reducing the pressure it exerts on the walls of the container.
Because this pressure depends on both the frequency and the intensity of collisions with the walls, the reduction in pressure is proportional to the square of the number of molecules per volume of space, and thus for a fixed number of molecules such as one mole, the reduction in pressure is inversely proportional to the square of the volume of the gas. The smaller the volume, the closer are the molecules and the greater will be the effect. The van der Waals equation replaces the \(P\) term in the ideal gas equation with \(P + (a / V^2)\) in which the magnitude of the constant a increases with the strength of the intermolecular attractive forces.
The complete van der Waals equation of state can be written as
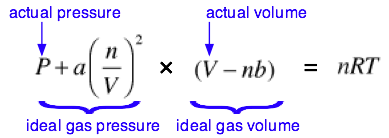
Although most students are not required to memorize this equation, you are expected to understand it and to explain the significance of the terms it contains. You should also understand that the van der Waals constants \(a\) and \(b\) must be determined empirically for every gas. This can be done by plotting the P-V behavior of the gas and adjusting the values of a and b until the van der Waals equation results in an identical plot. The constant \(a\) is related in a simple way to the molecular radius; thus the determination of \(a\) constitutes an indirect measurement of an important microscopic quantity.
|
Substance
|
molar mass, g |
a (L2-atm mole–2)
|
b (L mol–1)
|
|---|---|---|---|
| hydrogen H2 | 2 | 0.244 | 0.0266 |
| helium He | 4 | 0.034 | 0.0237 |
| methane CH4 | 16 | 2.25 | 0.0428 |
| water H2O | 18 | 5.46 | 0.0305 |
| nitrogen N2 | 28 | 1.39 | 0.0391 |
| carbon dioxide CO2 | 44 | 3.59 | 0.0427 |
| carbon tetrachloride CCl4 | 154 | 20.4 | 0.1383 |
The van der Waals equation is only one of many equations of state for real gases. More elaborate equations are required to describe the behavior of gases over wider pressure ranges. These generally take account of higher-order nonlinear attractive forces, and require the use of more empirical constants. Although we will make no use of them in this course, they are widely employed in chemical engineering work in which the behavior of gases at high pressures must be accurately predicted.
Contributors and Attributions
Stephen Lower, Professor Emeritus (Simon Fraser U.) Chem1 Virtual Textbook

