3.5: Optical Isomerism in Metal Complexes
- Page ID
- 81850
Optical isomers are stereoisomers that are related via non-superimposable mirror images of each other. They differ from geometric stereoisomers in that they rotate the polarization of plane-polarized light. These isomers are referred to as enantiomers or chiral.
Introduction
Optical activity refers to whether or not a compound has optical isomers. A coordinate compound that is optically active has optical isomers and a coordinate compound that is not optically active does not have optical isomers. As we will discuss later, optical isomers have the unique property of rotating light. When light is shot through a polarimeter, optical isomers can rotate the light so it comes out in with a different polarization on the other end. Armed with the knowledge of symmetry and mirror images, optical isomers should not be very difficult. There are two ways optical isomers can be determined: using mirror images or using planes of symmetry.
Optical isomers do not exhibit symmetry and do not have identical mirror images. Let's go through a quick review of symmetry and mirror images. A mirror image of an object is that object flipped or the way the object would look in front of a mirror. For example, the mirror image of your left hand would be your right hand. Symmetry on the other hand refers to when an object looks exactly the same when sliced in a certain direction with a plane. For example imagine the shape of a square. No matter in what direction it is sliced, the two resulting images will be the same.
What is a Polarimeter?
A polarimeter is a scientific instrument used to measure the angle of rotation caused by passing polarized light through an optically active substance. Some chemical substances are optically active, and polarized (uni-directional) light will rotate either to the left (counter-clockwise) or right (clockwise) when passed through these substances. The amount by which the light is rotated is known as the angle of rotation. The polarimeter is made up of a polarizer (#3 on Figure \(\PageIndex{1}\)) and an analyzer (#7 on Figure \(\PageIndex{1}\)). The polarizer allows only those light waves which move in a single plane. This causes the light to become plane polarized. When the analyzer is also placed in a similar position it allows the light waves coming from the polarizer to pass through it. When it is rotated through the right angle no waves can pass through the right angle and the field appears to be dark. If now a glass tube containing an optically active solution is placed between the polarizer and analyzer the light now rotates through the plane of polarization through a certain angle, the analyzer will have to be rotated in same angle.
.svg.png?revision=1&size=bestfit&width=601&height=334)
Chemists use polarimeters to investigate the influence of compounds (in the sample cell) on plane polarized light. Samples composed only of achiral molecules (e.g. water or hexane), have no effect on the polarized light beam. However, if a single enantiomer is examined (all sample molecules being right-handed, or all being left-handed), the plane of polarization is rotated in either a clockwise (positive) or counter-clockwise (negative) direction, and the analyzer must be turned an appropriate matching angle, α, if full light intensity is to reach the detector. In the above illustration, the sample has rotated the polarization plane clockwise by +90º, and the analyzer has been turned this amount to permit maximum light transmission.
The observed rotations (α) of enantiomers are opposite in direction. One enantiomer will rotate polarized light in a clockwise direction, termed dextrorotatory or (+), and its mirror-image partner in a counter-clockwise manner, termed levorotatory or (–). The prefixes dextro and levo come from the Latin dexter, meaning right, and laevus, for left, and are abbreviated d and l respectively. A 50:50 mixture of enantiomers has no observable optical activity. Such mixtures are called racemates or racemic modifications.
The "Mirror Image Method" to Determine Optical Isomers
Optical isomers do not exhibit symmetry and do not have identical mirror images. Let's go through a quick review of symmetry and mirror images. A mirror image of an object is that object flipped or the way the object would look in front of a mirror. For example, the mirror image of your left hand would be your right hand. Symmetry on the other hand refers to when an object looks exactly the same when sliced in a certain direction with a plane. For example imagine the shape of a square. No matter in what direction it is sliced, the two resulting images will be the same.
The mirror image method uses a mirror image of the molecule to determine whether optical isomers exist or not. If the mirror image can be rotated in such a way that it looks identical to the original molecule, then the molecule is said to be superimposable and has no optical isomers. On the other hand, if the mirror image cannot be rotated in any way such that it looks identical to the original molecule, then the molecule is said to be non-superimposable and the molecule has optical isomers. Once again, if the mirror image is superimposable, then no optical isomers, but if the mirror image is non-superimposable, then optical isomers exist.
Non-superimposable means the structure cannot be rotated in a way that one can be put on top of another. This means that no matter how the structure is rotated, it cannot be put on top of another with all points matching. An example of this is your hands. Both left and right hands are identical, but they cannot be put on top of each other with all points matching.
Non-superimposable means the structure cannot be rotated in a way that one can be put on top of another.
Example \(\PageIndex{1}\): The \(\ce{[OsCl_3(CO)_3]^{-}}\) Ion
Are there enantiomers for the \(fac-\ce{[OsCl3(CO)3]^{-}}\) complex ion?
Solution
To use mirror image method, we draw the 3D structure for this geometric isomer (not the mer isomer) and then take a mirror image like below.
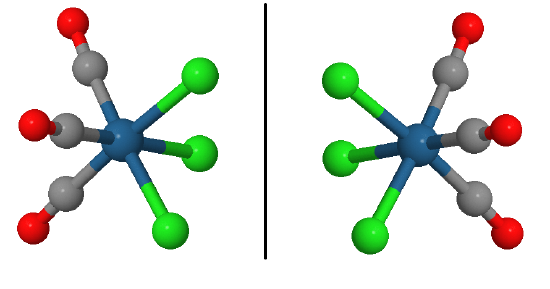
The left image can be rotated by 180° through a vertical axis to superimpose on the orginal. So the mer-\(\ce{[OsCl_3(CO)_3]^{-}}\) complex ion is not optically active or we can call it achiral.
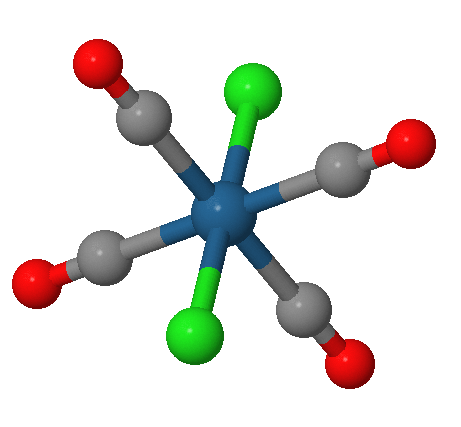
Exercise \(\PageIndex{1}\)
Use the mirror image method to determine if there are enantiomers for the \(\ce{mer-[OsCl_3(CO)_3]^{-}}\) complex ion.
Example \(\PageIndex{2}\)
Consider the octahedral complex with six monodentate ligands \(\ce{MA_2B_2C_2}\) have both cis and trans isomers. However, the cis isomer will also have two optical isomers (Figure \(\PageIndex{2}\)). No matter how one rotates one of the mirror images, they are are not superimposable.
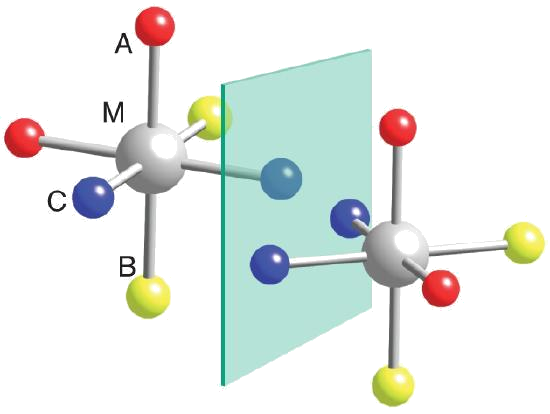
Exercise \(\PageIndex{1}\): \(\ce{MA2B2C2}\)
Confirm to yourself that if two like ligands in \(\ce{MA2B2C2}\) are trans to each other, then the complex will not have an optical isomer.
- Answer
-
If two like ligands are trans then there will be a mirror plane of symmetry normal to the line connecting the ligands that are trans to each other. The presence of the mirror plane means this complex will not have an optical isomer.
The "Plane of Symmetry Method" to Determine Optical Isomers
The plane of symmetry method uses symmetry also to identify optical isomers. In this method, one tries to see if such a plane exists which when cut through the coordinate compound produces two exact images. In other words, one looks for the existence of a plane of symmetry within the coordinate compound. If a plane of symmetry exists, then no optical isomers exist for that complex and it is called achiral.
Example \(\PageIndex{3}\): A Tetrahedral Complex
Consider the tetrahedral molecule, CHBrClF. Is this molecule optically active?
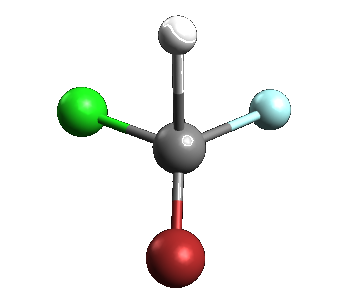
The CHBrClF molecule (note the color scheme: grey=carbon, white=hydrogen, green=chlorine, blue=fluorine, red=bromine)
Solution
- Mirror-image method
First take the Mirror-image method. The mirror image of the molecule is:
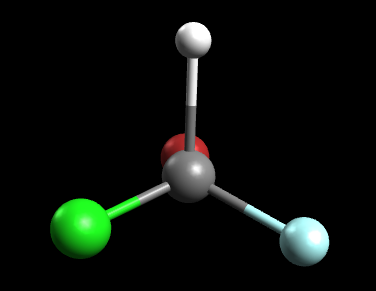
Note that this mirror image is not superimposable. In other words, the mirror image above cannot be rotated in any such way that it looks identical to the original molecule. Remember, if the mirror image is not superimposable, then optical isomers exist. Thus we know that this molecule has optical isomers.
- Plane of Symmetry Method
Let's try approaching this problem using the symmetry method. If we take the original molecule and draw an axis or plane of symmetry down the middle, this is what we get:
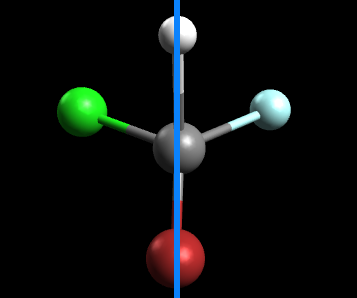
Since the left side is not identical to the right, this molecule does not have a symmetrical center and thus can be called chiral.Additionally, because it does not have a symmetrical center, we can conclude that this molecule has optical isomers. In general, when dealing with a tetrahedral molecule that has 4 different ligands, optical isomers will exist most of the time.
No matter which method you use, the answer will end up being the same.
Optical isomers have no plane of symmetry. For tetrahedral complexes, this is fairly easy to recognize the possibility of this by looking for a center atom with four different things attached to it. Unfortunately, this is not quite so easy with more complicated geometries!
Example \(\PageIndex{4}\): An Octahedral Complex
Is the octahedral compound \(\ce{FeCl3F3}\) optically active?
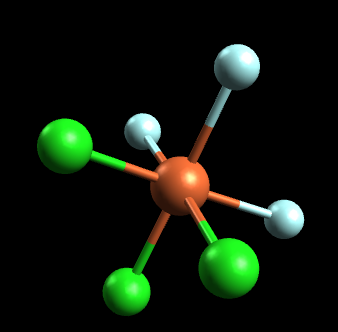
(note the color scheme: orange=iron, blue=fluorine, green=chlorine):
Solution
If we try to attempt this problem using the mirror image method, we notice that the mirror image is essentially identical to the original molecule. In other words, the mirror image can be placed on top of the original molecule and is thus superimposable. Since the mirror image is superimposable, this molecule does not have any optical isomers. Let's attempt this same problem using the symmetry method. If we draw an axis or plane of symmetry, this is what we get:
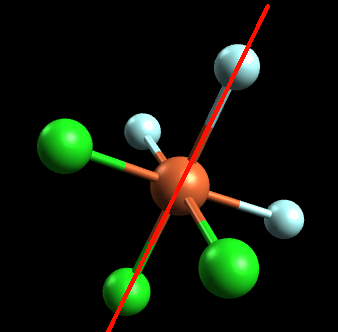
Since the left side is identical to the right side, this molecule has a symmetrical center and is an achiral molecule. Thus, it has no optical isomers.
Enantiomers in Octahedral Complexes with Bidentate Ligands
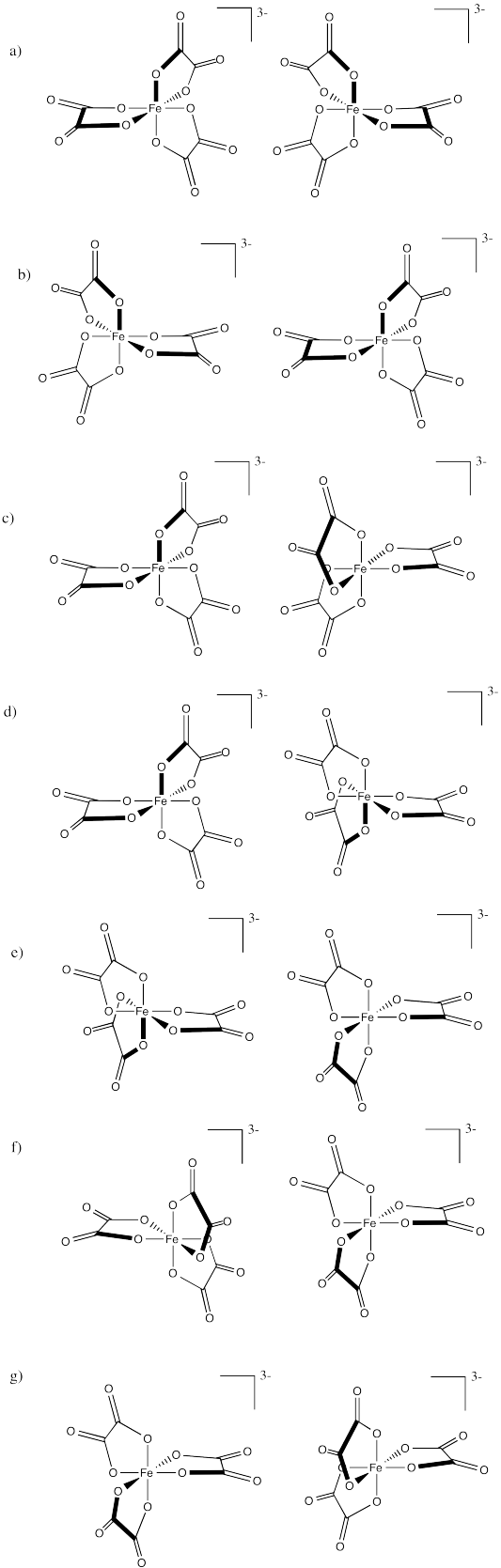
The examples you are most likely to need occur in octahedral complexes that contain bidentate ligands, e.g., complex ions like \(\ce{[Ni(NH_2CH_2CH_2NH_2)_3]^{2+}}\) or \(\ce{[Cr(C_2O_4)_3]^{3-}}\). In bidentate complexes or chelating complexes, a ligand binds very tightly to the metal because it holds onto the metal via more than one atom. Ethylenediamine is one example of a bidentate ligand.

As you may expect, bidentate ligands bind tightly to metals because they form two bonds with it, rather than just one. It is also important to recognize that in an octahedral complex, the two donor atoms in most bidentate ligand bind cis to each other and cannot reach all the way around the molecule to bind trans to each other (see below). The diagram below shows a simplified view of one of the complex ions with three oxalato ligands (also a bidentate ligand), however, they all have the same shape - all that differs is the nature of the "headphones".
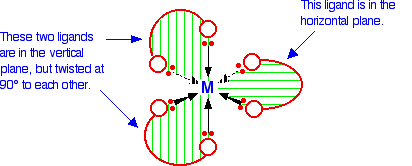
A substance with no plane of symmetry is going to have optical isomers - one of which is the mirror image of the other. One of the isomers will rotate the plane of polarization of plane polarized light clockwise; the other rotates it counter-clockwise. In this case, the two isomers are:
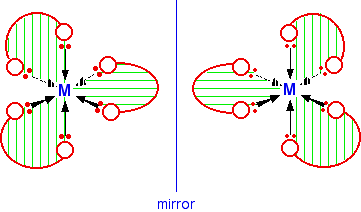
Most, but not all, Bidentate Ligands Bind to Metals in the cis Orientation
A wide variety of bidentate ligands bind to metals in the cis fashion, but few can bind in the trans geometry. These are called trans-spanning ligands and required building a bridge between the bonding atoms (e.g. methylene brindges \(\ce{-CH2CH2CH2CH2 -}\)).
We will not consider any trans-spanning ligands in this text.
A complex containing three bidentate ligands can take on the shape of a left-handed propeller or a right-handed propeller. You may be able to see that there is no way of rotating the second isomer in space so that it looks exactly the same as the first one. As long as you draw the isomers carefully, with the second one a true reflection of the first, the two structures will be different.
These kinds of complexes were historically important in demonstrating how small molecules and ions bound to metal cations. By showing that some metal complexes were chiral and displayed optical activity, early 20th century workers such as Alfred Werner were able to rule out some competing ideas about the structures of metal compounds. Today, we know that metal complexes play important roles in enzymes in biology, and Werner's work on metal complexes laid the groundwork for how we think about these complexes. In addition, stereochemistry in metal complexes became very important in the late 20th century, especially as pharmaceutical companies looked for catalysts that could aid in the production of one enantiomer of a drug, and not the other, in order to maximize pharmaceutical effectiveness and minimize side effects.
Contributors and Attributions
Prof. Robert J. Lancashire (The Department of Chemistry, University of the West Indies)
Jim Clark (Chemguide.co.uk)
Chris P Schaller, Ph.D., (College of Saint Benedict / Saint John's University)