13.7: Osmotic Pressure
- Page ID
- 42238
- To describe the relationship between solute concentration and the physical properties of a solution.
- To understand that the total number of nonvolatile solute particles determines the decrease in vapor pressure, increase in boiling point, and decrease in freezing point of a solution versus the pure solvent.
Osmotic pressure is a colligative property of solutions that is observed using a semipermeable membrane, a barrier with pores small enough to allow solvent molecules to pass through but not solute molecules or ions. The net flow of solvent through a semipermeable membrane is called osmosis (from the Greek osmós, meaning “push”). The direction of net solvent flow is always from the side with the lower concentration of solute to the side with the higher concentration.
Osmosis can be demonstrated using a U-tube like the one shown in Figure \(\PageIndex{1}\), which contains pure water in the left arm and a dilute aqueous solution of glucose in the right arm. A net flow of water through the membrane occurs until the levels in the arms eventually stop changing, which indicates that equilibrium has been reached. The osmotic pressure (\(\Pi\)) of the glucose solution is the difference in the pressure between the two sides, in this case the heights of the two columns. Although the semipermeable membrane allows water molecules to flow through in either direction, the rate of flow is not the same in both directions because the concentration of water is not the same in the two arms. The net flow of water through the membrane can be prevented by applying a pressure to the right arm that is equal to the osmotic pressure of the glucose solution.
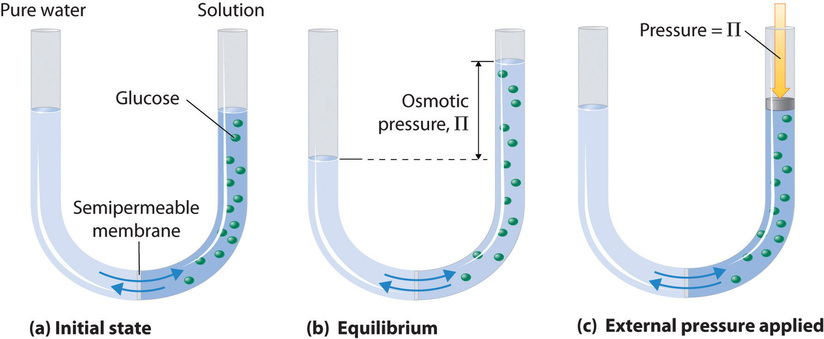
The osmotic pressure of a solution depends on the concentration of dissolved solute particles. Osmotic pressure obeys a law that resembles the ideal gas equation:
\[ \Pi=\dfrac{nRT}{V}=MRT \label{eq1}\]
where
- \(M\) is the number of moles of solute per unit volume of solution (i.e., the molarity of the solution),
- \(R\) is the ideal gas constant, and
- \(T\) is the absolute temperature.
As shown in Example \(\PageIndex{1}\), osmotic pressures tend to be quite high, even for rather dilute solutions.
When placed in a concentrated salt solution, certain yeasts are able to produce high internal concentrations of glycerol to counteract the osmotic pressure of the surrounding medium. Suppose that the yeast cells are placed in an aqueous solution containing 4.0% \(NaCl\) by mass; the solution density is 1.02 g/mL at 25°C.
Calculate the osmotic pressure of a 4.0% aqueous \(NaCl\) solution at 25°C.
If the normal osmotic pressure inside a yeast cell is 7.3 atm, corresponding to a total concentration of dissolved particles of 0.30 M, what concentration of glycerol must the cells synthesize to exactly balance the external osmotic pressure at 25°C?
Given: concentration, density, and temperature of \(NaCl\) solution; internal osmotic pressure of cell
Asked for: osmotic pressure of \(NaCl\) solution and concentration of glycerol needed
Strategy:
- Calculate the molarity of the \(NaCl\) solution using the formula mass of the solute and the density of the solution. Then calculate the total concentration of dissolved particles.
- Use Equation \ref{eq1} to calculate the osmotic pressure of the solution.
- Subtract the normal osmotic pressure of the cells from the osmotic pressure of the salt solution to obtain the additional pressure needed to balance the two. Use Equation \ref{eq1} to calculate the molarity of glycerol needed to create this osmotic pressure.
Solution:
A The solution contains 4.0 g of \(NaCl\) per 100 g of solution. Using the formula mass of \(NaCl\) (58.44 g/mol) and the density of the solution (1.02 g/mL), we can calculate the molarity:
\[\begin{align} M_{NaCl} &=\dfrac{moles\; NaCl}{\text{liter solution}} \nonumber \\[4pt] &=\left(\dfrac{4.0 \; \cancel{g} \;NaCl}{58.44\; \cancel{g}/mol\; NaCl}\right)\left(\dfrac{1}{100\; \cancel{g \;solution}}\right)\left(\dfrac{1.02\; \cancel{g\; solution}}{1.00\; \cancel{mL}\; solution}\right)\left(\dfrac{1000\; \cancel{mL}}{1\; L}\right) \nonumber \\[4pt] &= 0.70\; M\; NaCl \nonumber \end{align} \nonumber\]
Because 1 mol of \(NaCl\) produces 2 mol of particles in solution, the total concentration of dissolved particles in the solution is (2)(0.70 M) = 1.4 M.
B Now we can use Equation \ref{eq1} to calculate the osmotic pressure of the solution:
\[\begin{align*} \Pi &=MRT \\[4pt] &=(1.4 \;mol/L)\left[ 0.0821\; (L⋅atm)/(K⋅mol) \right ] (298\; K) \\[4pt] &= 34 \;atm \end{align*}\]
C If the yeast cells are to exactly balance the external osmotic pressure, they must produce enough glycerol to give an additional internal pressure of (34 atm − 7.3 atm) = 27 atm. Glycerol is a nonelectrolyte, so we can solve Equation \ref{eq1} for the molarity corresponding to this osmotic pressure:
\[\begin{align*} M &=\dfrac{\Pi}{RT} \\[4pt] &= \dfrac{27\; \cancel{atm}}{[0.0821(L⋅\cancel{atm})/(\cancel{K}⋅mol)] (298 \;\cancel{K})} \\[4pt] &= 1.1 \;M \;glycerol \end{align*}\]
In solving this problem, we could also have recognized that the only way the osmotic pressures can be the same inside the cells and in the solution is if the concentrations of dissolved particles are the same. We are given that the normal concentration of dissolved particles in the cells is 0.3 M, and we have calculated that the \(NaCl\) solution is effectively 1.4 M in dissolved particles. The yeast cells must therefore synthesize enough glycerol to increase the internal concentration of dissolved particles from 0.3 M to 1.4 M—that is, an additional 1.1 M concentration of glycerol.
Assume that the fluids inside a sausage are approximately 0.80 M in dissolved particles due to the salt and sodium nitrite used to prepare them. Calculate the osmotic pressure inside the sausage at 100°C to learn why experienced cooks pierce the semipermeable skin of sausages before boiling them.
Answer: 24 atm
Because of the large magnitude of osmotic pressures, osmosis is extraordinarily important in biochemistry, biology, and medicine. Virtually every barrier that separates an organism or cell from its environment acts like a semipermeable membrane, permitting the flow of water but not solutes. The same is true of the compartments inside an organism or cell. Some specialized barriers, such as those in your kidneys, are slightly more permeable and use a related process called dialysis, which permits both water and small molecules to pass through but not large molecules such as proteins.
The same principle has long been used to preserve fruits and their essential vitamins over the long winter. High concentrations of sugar are used in jams and jellies not for sweetness alone but because they greatly increase the osmotic pressure. Thus any bacteria not killed in the cooking process are dehydrated, which keeps them from multiplying in an otherwise rich medium for bacterial growth. A similar process using salt prevents bacteria from growing in ham, bacon, salt pork, salt cod, and other preserved meats. The effect of osmotic pressure is dramatically illustrated in Figure \(\PageIndex{2}\), which shows what happens when red blood cells are placed in a solution whose osmotic pressure is much lower or much higher than the internal pressure of the cells.

In addition to capillary action, trees use osmotic pressure to transport water and other nutrients from the roots to the upper branches. Evaporation of water from the leaves results in a local increase in the salt concentration, which generates an osmotic pressure that pulls water up the trunk of the tree to the leaves.
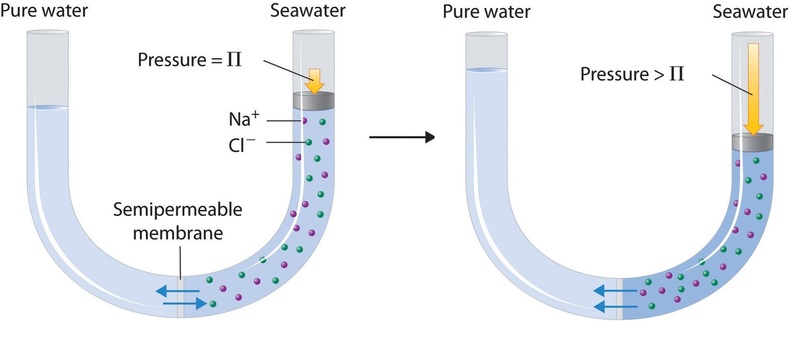
Finally, a process called reverse osmosis can be used to produce pure water from seawater. As shown schematically in Figure \(\PageIndex{3}\), applying high pressure to seawater forces water molecules to flow through a semipermeable membrane that separates pure water from the solution, leaving the dissolved salt behind. Large-scale desalinization plants that can produce hundreds of thousands of gallons of freshwater per day are common in the desert lands of the Middle East, where they supply a large proportion of the freshwater needed by the population. Similar facilities are now being used to supply freshwater in southern California. Small, hand-operated reverse osmosis units can produce approximately 5 L of freshwater per hour, enough to keep 25 people alive, and are now standard equipment on US Navy lifeboats.
Osmotic Pressure: https://youtu.be/uYQxI4mi3DA
Summary
When a solution and a pure solvent are separated by a semipermeable membrane, a barrier that allows solvent molecules but not solute molecules to pass through, the flow of solvent in opposing directions is unequal and produces an osmotic pressure, which is the difference in pressure between the two sides of the membrane. Osmosis is the net flow of solvent through such a membrane due to different solute concentrations. Dialysis uses a semipermeable membrane with pores that allow only small solute molecules and solvent molecules to pass through.

