1.1: Electromagnetic Radiation (Component 1)

Spectroscopy is the study of the interaction of radiation with matter. Electromagnetic radiation is a form of energy that is produce by oscillating electric and magnetic disturbance. It travels at the speed of light as a quantized harmonic wave. The electric and magnetic waves travel perpendicular to each other. Characteristics of waves include amplitude, wavelength, and frequency.

The electromagnetic spectrum consists of Radio/TV, Microwaves, Infrared, Visible, Ultraviolet, X-rays, and Gamma-rays (Figure \(\PageIndex{1}\)). The longest waves, radio waves, are approximately 10³ m in wavelength. As the name implies, radio waves are transmitted by radio broadcasts, TV broadcasts, and even cell phones. The shortest waves, Gamma rays, are approximately 10^-12 m in wavelength. Out this huge spectrum, the human eyes can only detect waves from 390 nm to 780 nm.

Figure \(\PageIndex{1}\): The Electromagnetic Spectrum. (a) This diagram shows the wavelength and frequency ranges of electromagnetic radiation. The visible portion of the electromagnetic spectrum is the narrow region with wavelengths between about 400 and 700 nm. (b) When white light is passed through a prism, it is split into light of different wavelengths, whose colors correspond to the visible spectrum. (CC BY-NC-SA; anonymous)

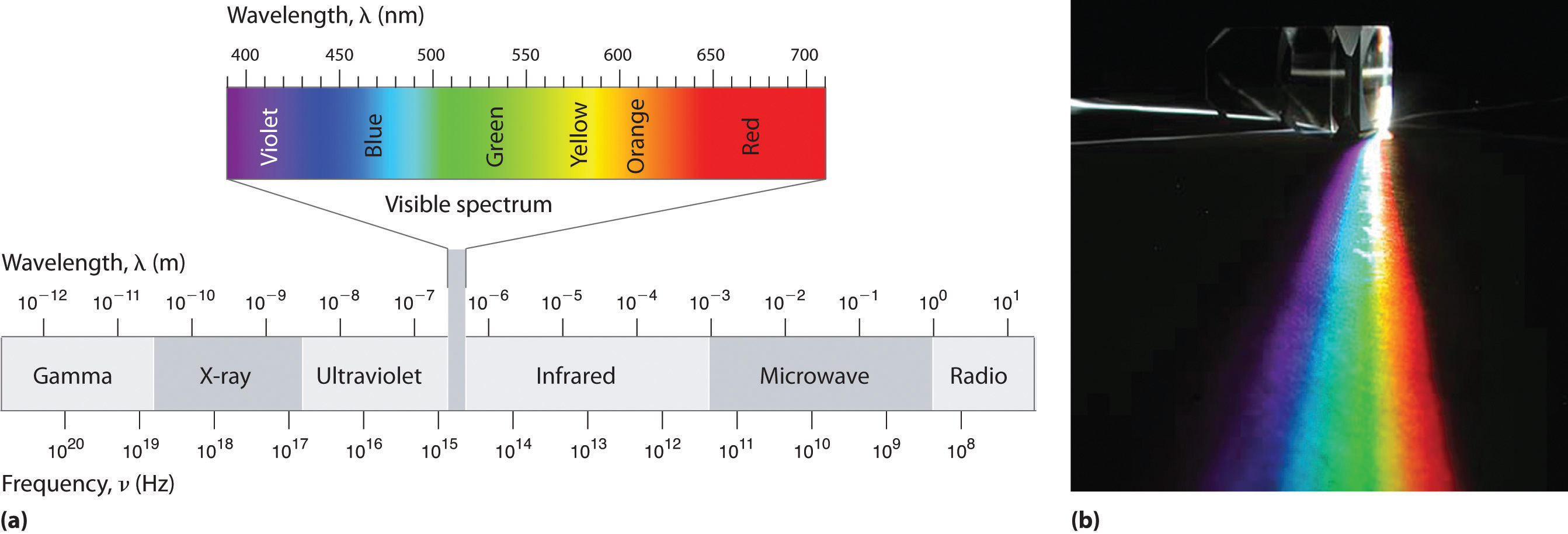
Within this visible range our eyes perceive radiation of different wavelengths (or frequencies) as light of different colors, ranging from red to violet in order of decreasing wavelength. The components of white light—a mixture of all the frequencies of visible light—can be separated by a prism (Figure \(\PageIndex{1b}\)). A similar phenomenon creates a rainbow, where water droplets suspended in the air act as tiny prisms.

Table \(\PageIndex{1}\): Common Wavelength Units for Electromagnetic Radiation

Unit	Symbol	Wavelength (m)	Type of Radiation
picometer	pm	10^−12	gamma ray
angstrom	Å	10^−10	x-ray
nanometer	nm	10^−9	x-ray
micrometer	μm	10^−6	infrared
millimeter	mm	10^−3	infrared
centimeter	cm	10^−2	microwave
meter	m	10^0	radio

We know that EM radiation of photons whose energy each with energies given by Planck’s law:

\[E = hv \label{eq5} \]

where \(h\) is Planck’s constant = \(6.626068 \times 10^{-34} \;m^2 kg/s\) and \(\nu\) is the frequency (\(1/s\) or \(Hz\)).

The speed of the electromagnetic radiation in vacuum is \(c\), which is equal to 299,792,458 m/s. Since

\[c = \lambda \nu \nonumber \]

EEquation \ref{eq5} can be written in the following two alternate forms:

\[E = \dfrac{hc}{\lambda} = hc\tilde{\nu} \nonumber \]

or

\[\tilde{\nu} = \dfrac{1}{\lambda}. \nonumber \]

where \(1/\lambda\) is the inverse wavelength or wavenumber (cm^-1).

The effect that a photon will have on matter or molecule will depend on \(E\), and thus on \(v\).

• For \(\tilde{\nu}\) < 10^-2 cm^-1 (λ ~ 1 m), we have radio frequencies. These are too low an energy photons for anything except to affect the magnetic energy of a nucleus in an external magnetic field (NMR Spectroscopy)
• For 10^-2 cm^-1 < \(\tilde{\nu}\) < 10 cm^-1 (λ ~ 1 cm ), we have microwave frequencies. Photons have enough energy to be absorbed by unpaired electrons spins in an externally magnetic field (ESR) or to change the rotational energy of a molecule (microwave rotational spectroscopy)
• For 10 cm^-1 < \(\tilde{\nu}\) < 10⁴ cm^-1 (λ ~ 5 μm ), we have infrared frequencies. Photons have sufficient energy to be absorbed in the rotational motion of the molecules. This is called vibrational spectroscopy.
• For 10^-2 cm^-1 < \(\tilde{\nu}\) < 10⁵ cm^-1 (λ < 1 μm ), we have visible and UV spectroscopy which involves excitations of electrons (valence) from stable orbits to higher energy orbits in the molecule. Electronic spectroscopy (UV-VIS)
• For 10⁵ cm^-1 < \(\tilde{\nu}\) < 10⁶ cm^-1, we have vacuum UV, where the photons have enough energy that if absorbed by a valence electron, the electron can be “knocked” out of the molecule. This is called photoelectron spectroscopy
• For 10⁶ cm^-1 < \(\tilde{\nu}\) < 10⁸ cm^-1, these are X-rays and have enough energy to ionize not only valence electrons, but also core electrons. This spectroscopy is call X-ray Photo-electron spectroscopy (XPS) and also Extended X-ray absorption fine structure (EXAFS) and X-ray Absorption Near Edge Structure (XANES).
• For \(\tilde{\nu}\) < 10⁸ cm^-1. These are very energetic gamma rays and are not used extensively for spectroscopy with chemists. One key exception is Mössbauer spectroscopy which is enough energy to promote changes in the nuclei of the atoms.

That is a quick run-down of the spectroscopies we will be address in this course. We will not be discussing mass spectroscopy or diffraction techniques although used quite constructively for many scientific endeavors.