2015 Final 2 Solutions

Q8.

Consider the ground state of H₂⁺ with the nuclei at their equilibrium separation, 1.06 angstrom.

1. (5 points) Write a full Hamiltonian for this system

\[H=-\dfrac{\hbar^2}{2m}\nabla^2-\dfrac{e^2}{4\pi\epsilon r_A}-\dfrac{e^2}{4\pi\epsilon r_B}+\dfrac{e^2}{4\pi\epsilon R}\]

where \(r_A,\ r_B\) are the distances between the electron and nuclei, and \(R\) is the distance between the nuclei.

2. (5 points) We approximate wave function for the ground electronic state has the general form \(\psi=1S_A+1S_B\) where the internuclear distance is treated as a fixed parameter. What does 1s represent?

Ground-state atomic orbital of hydrogen.

3. (5 points) To what do the labels A and B refer?

Nucleus A and nucleus B.

4. (5 points) How many independent spatial coordinates appear in our approximate \(\psi\)?

Two: \(r_A,\ r_B\).

5. (5 points) Derive the normalization constant for this wavefunction?

\[\int \psi ^* \psi d\tau = \left \langle \psi | \psi \right \rangle = 1 \]

\[\left \langle C_{+} [ 1s_A + 1s_B ] | C_{+} [ 1s_A + 1s_B ]\right \rangle = 1 \]

\[|C_{+}|^2 [ \left \langle1s_A | 1s_A\right \rangle + \left \langle1s_B | 1s_B\right \rangle + \left \langle 1s_B | 1s_A\right \rangle + \left \langle1s_A | 1s_B\right \rangle] = 1 \]

\(1s\) wavefunctions are real so

\[ \left \langle 1s_A | 1s_B \right \rangle = \left \langle 1s_B | 1s_A \right \rangle = S \]

Plug \(S\) in

\[|C_{+}|^2 (2 + 2S ) = 1 \]

\[C_{+} = \dfrac{1}{\sqrt{2(1 + S )}} \]

6. (5 points) Sketch the values of \(\psi\) along the internuclear axis.

The green curve in the figure below.

---

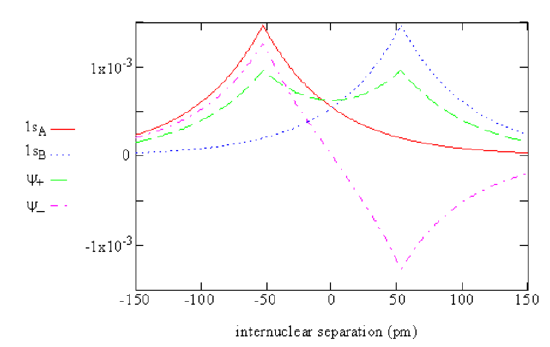
Q9.

The fundamental vibrational frequencies for ¹H¹⁹F and ²D¹⁹F are 4138.52 and 998.25 cm^-1, respectively, in the harmonic oscillator model. D_e for both molecules is 5.86 eV. The figure shows two possible potential energy curves for these two molecules.

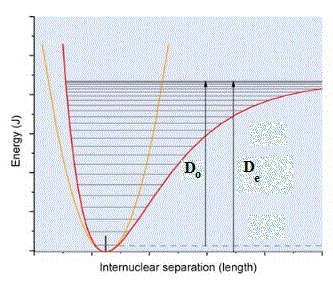
a. (2 points) Label the axes of the figure and give units.

It is partially done, however, the units of internuclear separation remain to be added (angstroms, nanometers, picometers, micrometers, centimeters, meters, etc.)

b. (4 points) Which potential surface better describes the vibration of the two molecules and why?

The red potential better describes the vibration of the two molecules because it shows that the force that holds the nuclei at a certain distance becomes weaker when the distance increases.

c. (3 points) Define D_e for the red potential.

D_e is the depth of the potential well.

d. (3 points) Write the chemical reaction that can be used to define the bond energy of ¹H¹⁹F.

HF(g)→H^•(g)+F^•​(g)

e. (3 points) What is the ground state (vibrational) energy of ¹H¹⁹F ?

\[E_0^H=\dfrac{h\nu}{2}\]

\[E_0^H=\dfrac{6.63×10^{-34} \ J×s \ ×3×10^{10}\ \dfrac{cm}{s} \ ×4138.52 \ cm^{-1}}{2}=4.1×10^{-20} \ J\]

or

\[E_0^H=\dfrac{4138.52}{2} \ cm^{-1}= 2069.26 \ cm^{-1} \]

f. (3 points) What is the ground state (vibrational) energy of ²D¹⁹F ?

\[E_0^D=\dfrac{h\nu}{2}\]

\[E_0^D=\dfrac{6.63×10^{-34} \ J×s \ ×3×10^{10}\ \dfrac{cm}{s} \ × 998.25 \ cm^{-1}}{2}=9.9×10^{-21} \ J\]

or

\[E_0^D=\dfrac{998.25}{2} \ cm^{-1}= 499.125 \ cm^{-1} \]

g. (4 points) What is the bond energy of ¹H¹⁹F ?

\[BE^H=D_e-E_0^H= 1.6×10^{-19} \ \dfrac{J}{eV} ×5.86 \ eV \ - 4.1×10^{-20} \ J = 8.9×10^{-19} \ J\]

or

\[BE^H=D_e-E_0^H= 5.86 \ eV \ - \dfrac{4.1×10^{-20} \ J}{1.6×10^{-19} \ \dfrac{J}{eV} } = 5.60 \ eV\]

f. (4 points) What is the bond energy of ²D¹⁹F ?

\[BE^D=D_e-E_0^D= 1.6×10^{-19} \ \dfrac{J}{eV} ×5.86 \ eV \ - 9.9×10^{-21} \ J = 9.2×10^{-19} \ J\]

or

\[BE^D=D_e-E_0^D= 5.86 \ eV \ - \dfrac{9.9×10^{-21} \ J}{1.6×10^{-19} \ \dfrac{J}{eV} } = 5.79 \ eV\]

i. (4 points) Which bond is stronger and why?

The bond in ²D¹⁹F is stronger because the bond energy \(BE^D\) is greater.

Q10.

In perturbation theory, the only things that matters is the modified part of the Hamiltonian.

\[\hat{H}' = Ax^6 \tag{5 points}\]

The first order correction to the energy is

\[E' = <\psi|\hat{H}'|\psi> \tag{5 points}\]

\[E' = <(\dfrac{\alpha}{\pi})^{1/4} e^{-\alpha x^2 /2} |Ax^6|(\dfrac{\alpha}{\pi})^{1/4} e^{-\alpha x^2 /2}> \tag{5 points}\]

\[E' = <(\dfrac{\alpha}{\pi})^{1/2} e^{-\alpha x^2} Ax^6> \]

\[E' = (\dfrac{\alpha}{\pi})^{1/2} A 2 \int_0^\infty x^6 e^{-\alpha x^2} \tag {5 points}\]

\[E' = (\dfrac{\alpha}{\pi})^{1/2} A 2 (\dfrac{\pi}{\alpha})^{1/2} \dfrac{15}{16\alpha^3} \]

\[E' = A \dfrac{15}{8\alpha^3} \tag{5 points}\]

So the first order energy

\[E^1 = \hbar\omega (1/2 + v) + A \dfrac{15}{8\alpha^3} = \dfrac{\hbar\omega}{2}+ A \dfrac{15\hbar^3}{8\mu^3\omega^3} \tag{5 points}\]

Q11.

The most probable radius is the maximum of the probability distribution including the volume element.

For the H 1s orbital -

\[P dr = \psi*\psi = R(r)^2 Y_m^l (\theta, \phi)^2 r^2 sin \theta dr d\theta d\phi \tag{2 points}\]

Integrating over the volume element leaves

\[P dr = R(r)^2 Y_m^l (\theta, \phi)^2 r^2 dr \int_{-\infty}^{\infty} sin \theta d\theta d\phi = R(r)^2 Y_m^l (\theta, \phi)^2 r^2 dr \times 4\pi \tag{3 points}\]

Inserting the 1s wavefunction

\[P = 4\pi \times r^2 \times \dfrac{1}{\pi} \dfrac{1}{a_0^3} e^{-2r/a_0} \]

\[P = r^2 \dfrac{4}{a_0^3} e^{-2r/a_0} \]

\[\dfrac{d}{dr} P = 2r \dfrac{4}{a_0^3} e^{-2r/a_0} + r^2 \dfrac{4}{a_0^3} \dfrac{-2}{a_0} e^{-2r/a_0}\]

\[\dfrac{d}{dr} P = \dfrac{8}{a_0^3} e^{-2r/a_0} r [1-\dfrac{r}{a_0}] \tag{3 points}\]

So the function equals zero at

\[r = 0, a_0 \]

\(r=0\) is a minimum and the answer is

\[r=a_0 \tag{2 points}\]

For the least probable location in 2s for He⁺

The 2s orbital has a node and will be the least probable location that is not at \(r=0 \) or \(r = \infty\) \[\tag{3 points}\]

\[\psi_{2s} = \dfrac{1}{\sqrt{32\pi}} (\dfrac{Z}{a_0})^{3/2} (2 - \dfrac{Zr}{a_0} ) e^{-\dfrac{Zr}{2a_0} } \tag{2 points}\]

This wavefunction will equal zero when

\[(2 - \dfrac{Zr}{a_0} ) = 0 \tag{3 points}\]

\[r= \dfrac{2a_0}{Z} = \dfrac{2a_0}{2} = a_0 \tag{3 points}\]

For the probability at a radius small than the node in 2s for Li²⁺ with the volume element

\[P = <\psi|\psi> = 4\pi \int_0^{\dfrac{2a_0}{3}} \dfrac{1}{\sqrt{32\pi}} (\dfrac{Z}{a_0})^{3/2} (2 - \dfrac{Zr}{a_0} ) e^{-\dfrac{Zr}{2a_0} } \]

\[\times \dfrac{1}{\sqrt{32\pi}} (\dfrac{Z}{a_0})^{3/2} (2 - \dfrac{Zr}{a_0} ) e^{-\dfrac{Zr}{2a_0} } r^2 dr \tag{3 points}\]

Where the limits of integration came from the previous question. The node is located at

\[r= \dfrac{2a_0}{Z} = \dfrac{2a_0}{3} \tag{2 points}\]

The final integral you were instructed not to solve is:

\[P = <\psi|\psi> = 4\pi \dfrac{1}{32\pi} (\dfrac{Z}{a_0})^3 \int_0^{\dfrac{2a_0}{3}} (2 - \dfrac{Zr}{a_0} )^2 e^{-\dfrac{Zr}{a_0} } r^2 dr \tag{5 points}\]