2015 Final 1 Solutions

Q1.

For a function to be an eigen function it must agree with this equation:

\[\hat{P}\psi = k\psi \tag{2 points}\]

\[\hat{P}\psi = \dfrac{d^2}{dx^2} Asin(nx) + Bcos(mx) \]

\[\hat{P}\psi = -n^2Asin(nx) - m^2Bcos(mx) \tag{2 points} \]

For this is be an eigenfunction

\[n^2=m^2=k \tag{3 points}\]

\[\hat{P}\psi = -k [Asin(nx) + Bcos(mx)] = -k\psi \]

\(A\) and \(B\) can be any value including zero. \(\tag{3 points}\)

Q2.

Boron has the configuration 1s²2s²2p¹

Filled orbitals do not contribute to the term symbol. \(\tag{2 points}\)

So only considering the 2p¹ electron we have

\[S = 1/2 \tag{2 points} \]

\[L = 1 \tag{2 points} \]

\[J = 3/2 , 1/2 \tag{2 points} \]

Therefore the term symbols are

²P_3/2 and ²P_1/2 \(\tag{2 points}\)

Q3.

Draw the proper wavefunctions and probabilities. \(\tag{2 points each}\)

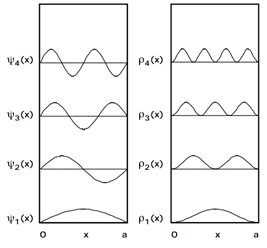
Because the Particle in a Box model is symmetric with respect to the center of the box the probability to be found in half of the box for any state is 1/2. \(\tag{2 points}\)

Q4.

To measure any observables simultaneously the operators must commute.

\[ [\hat{A} , \hat{B} ] = \hat{A}\hat{B}f(x) - \hat{B}\hat{A}f(x) \stackrel{?}{=} 0 \tag{2 points} \]

\[ = \dfrac{d}{dx} x^2 f(x) - x^2 \dfrac{d}{dx} f(x) \]

\[ = 2xf(x) - x^2 f'(x) \tag{4 points} \]

\[ [\hat{A} , \hat{B} ] \neq 0 \]

This means the operators do not commute, so the observables cannot be measured simultaneously. \(\tag{4 points}\)

Q5.

The bullet is an extremely large object, in quantum terms, so we would expect the uncertainty principle to have a very small impact.

\[\Delta p\Delta x \geq \dfrac{\hbar}{2} \tag{4 points} \]

\[\Delta p = mv \times uncertainty \tag{2 points} \]

\[\Delta x \geq \dfrac{\hbar}{2 \Delta p} = \dfrac{\hbar}{2mv\sigma} \tag{2 points}\]

Input the correct values and

\[\Delta x \geq 1.95 \times 10^{-33} m \tag{2 points} \]

Q6.

Rotational energy transition from \(J=0\) to \(J=1\) in NaH

The energy of the photon is equal to the difference in energy between the 2 levels.

\[E_{Rot} = BJ(J+1) \]

\[\Delta E_{Rot} = E_{photon} = 2B-0 \tag{3 points} \]

\[2B = \dfrac{2\hbar^2}{2I} = \dfrac{\hbar^2}{\mu r^2} = E_{photon} \]

\[\mu = \dfrac{m_{Na} \times m_{H}}{m_{Na} + m_{H}} \tag{1 point} \]

\[E_{photon} = h\nu \tag{1 point} \]

\[r = \sqrt{\dfrac{\hbar^2}{\mu\nu h}} \tag{2 points}\]

Input the correct values and

\[r = 1.89 \dot A \tag{3 points}\]

Q7.

Vibrational transition from \(v=0\) to \(v=1\) in the HF molecule.

\[E_{Vib} = \hbar\omega (1/2 + v) \]

\[\Delta E_{Vib} = \hbar\omega \tag{2 points} \]

\[\omega = \sqrt{\dfrac{k}{\mu}} \tag{1 points} \]

\[\mu = \dfrac{m_{F} \times m_{H}}{m_{F} + m_{H}} \tag{1 point} \]

With the proper numbers

\[\Delta E_{Vib} = \hbar\sqrt{\dfrac{k}{\mu}} = 8.41 \times 10^{-20} J \tag{3 points} \]

\[\Delta E_{Vib} = E_{photon} = \dfrac{hc}{\lambda} \]

With the correct values.

\[\lambda = \dfrac{hc}{\Delta E_{Vib}} = 2.36 \times 10^{-6} m = 2.36 \mu m \tag{3 points} \]

Q8.

What is the expectation for the electron probability density halfway between the two hydrogen nuclei for an electron in the first bonding molecular orbital compared to one in the first antibonding molecular orbital? You may use LCAO approximation for the molecular orbitals. Do not evaluate overlap, exchange and coulomb integrals if required.

The expression for bonding molecular orbital of \(H_2^{+}\) in LCAO approximation is

\[\psi_{H_2^{+}}=C_1\psi_{1s_A}+C_2\psi_{1s_B}=C_{+}(\psi_{1s_A}+\psi_{1s_B}) \tag{3 points} \]

where \(\psi_{1s_A}\) and \(\psi_{1s_B}\) are the atomic orbitals of an electron.

To use this wavefunction in calculation of electron probability density normalization is needed.

\[\int \psi ^*_{H_2^{+}} \psi _{H_2^{+}} d\tau = \left \langle \psi _{H_2^{+}} | \psi _{H_2^{+}} \right \rangle = 1 \]

\[\left \langle C_{+} [ \psi_{1s_A}+ \psi_{1s_B} ] | C_{+} [ \psi_{1s_A}+ \psi_{1s_B} ]\right \rangle = 1 \]

\[|C_{+}|^2 [\left \langle\psi_{1s_A} | \psi_{1s_A}\right \rangle + \left \langle\psi_{1s_B} | \psi_{1s_B}\right \rangle+ \left \langle\psi_{1s_B} | \psi_{1s_A}\right \rangle+ \left \langle\psi_{1s_A} | \psi_{1s_B}\right \rangle] = 1 \]

\(1s\) wavefunctions are real so

\[ \left \langle \psi_{1s_A} | \psi_{1s_B} \right \rangle = \left \langle \psi_{1s_B} | \psi_{1s_A} \right \rangle = S \]

Plug \(S\) in

\[|C_{+}|^2 (2 + 2S) = 1 \]

\[C_{+} = \dfrac{1}{\sqrt{2(1 + S)}} \tag{3 points} \]

The electron probability density is

\[\psi_{H_2^{+}}^*\psi_{H_2^{+}} \ (2 \ points) \ =C_{+}(\psi_{1s_A}+\psi_{1s_B})C_{+}(\psi_{1s_A}+\psi_{1s_B})=C_{+}^2(\psi_{1s_A}+\psi_{1s_B})^2=\dfrac{1}{2(1 + S)}(\psi_{1s_A}+\psi_{1s_B})^2\]

Plugs in the hydrogen like atomic wavefunction of the ground state in the expression for probability density

\[\psi_{H_2^{+}}^*\psi_{H_2^{+}}=\dfrac{1}{2(1 + S)}(\dfrac{1}{\sqrt{\pi}}(\dfrac{Z}{a_0})^\dfrac{3}{2}e^{-\dfrac{Zr_A}{a_0}}+\dfrac{1}{\sqrt{\pi}}(\dfrac{Z}{a_0})^\dfrac{3}{2}e^{-\dfrac{Zr_B}{a_0}})^2 \ (3 \ points) \ =\dfrac{1}{2\pi(1 + S)}(\dfrac{Z}{a_0})^{3}(e^{-\dfrac{Zr_A}{a_0}}+e^{-\dfrac{Zr_B}{a_0}})^2= \\ \dfrac{1}{2\pi(1 + S)}(\dfrac{Z}{a_0})^{3}(e^{-\dfrac{2Zr_A}{a_0}}+e^{-\dfrac{2Zr_B}{a_0}}+2e^{-\dfrac{Zr_A}{a_0}-\dfrac{Zr_B}{a_0}})\]

Since electron here is halfway between the two hydrogen nuclei \(r_A=r_B\)

\[\psi_{H_2^{+}}^*\psi_{H_2^{+}}=\dfrac{1}{2\pi(1 + S)}(\dfrac{Z}{a_0})^{3}(e^{-\dfrac{2Zr_A}{a_0}}+e^{-\dfrac{2Zr_B}{a_0}}+2e^{-\dfrac{Zr_A}{a_0}-\dfrac{Zr_B}{a_0}}) = \\ \dfrac{1}{2\pi(1 + S)}(\dfrac{Z}{a_0})^{3}(e^{-\dfrac{2Zr_A}{a_0}}+e^{-\dfrac{2Zr_A}{a_0}}+2e^{-\dfrac{Zr_A}{a_0}-\dfrac{Zr_A}{a_0}})= \\ \dfrac{1}{2\pi(1 + S)}(\dfrac{Z}{a_0})^{3}(2e^{-\dfrac{2Zr_A}{a_0}}+2e^{-\dfrac{2Zr_A}{a_0}})=\dfrac{2}{\pi(1 + S)}(\dfrac{Z}{a_0})^{3}e^{-\dfrac{2Zr_A}{a_0}} \ (4 \ points) \ \]

For antibonding molecular orbital there was no need to do such calculations. There is a node of the \(\psi_{H_2^{+}}\) wavefunction halfway between the two hydrogen nuclei. Therefore, the wavefunction as well as the electron probability density there is zero (15 points).

Alternative calculations for antibonding molecular orbital give the same result:

The expression for antibonding molecular orbital of \(H_2^{+}\) in LCAO approximation is

\[\psi_{H_2^{-}}=C_1\psi_{1s_A}-C_2\psi_{1s_B}=C_{-}(\psi_{1s_A}-\psi_{1s_B}) \tag{3 points} \]

where \(\psi_{1s_A}\) and \(\psi_{1s_B}\) are the atomic orbitals of an electron.

Normalization constant is

\[C_{-} = \dfrac{1}{\sqrt{2(1 - S)}} \tag{3 points} \]

The electron probability density is

\[\psi_{H_2^{+}}^*\psi_{H_2^{+}} \ (2 \ points) \ =\dfrac{1}{2(1 - S)}(\dfrac{1}{\sqrt{\pi}}(\dfrac{Z}{a_0})^\dfrac{3}{2}e^{-\dfrac{Zr_A}{a_0}}-\dfrac{1}{\sqrt{\pi}}(\dfrac{Z}{a_0})^\dfrac{3}{2}e^{-\dfrac{Zr_B}{a_0}})^2 \ (3 \ points) \ = \\ \dfrac{1}{2\pi(1 - S)}(\dfrac{Z}{a_0})^{3}(e^{-\dfrac{Zr_A}{a_0}}-e^{-\dfrac{Zr_B}{a_0}})^2= \\ \dfrac{1}{2\pi(1 - S)}(\dfrac{Z}{a_0})^{3}(e^{-\dfrac{2Zr_A}{a_0}}+e^{-\dfrac{2Zr_B}{a_0}}-2e^{-\dfrac{Zr_A}{a_0}-\dfrac{Zr_B}{a_0}})\]

Since electron here is halfway between the two hydrogen nuclei \(r_A=r_B\)

\[\psi_{H_2^{+}}^*\psi_{H_2^{+}}=\dfrac{1}{2\pi(1 - S)}(\dfrac{Z}{a_0})^{3}(e^{-\dfrac{2Zr_A}{a_0}}+e^{-\dfrac{2Zr_B}{a_0}}-2e^{-\dfrac{Zr_A}{a_0}-\dfrac{Zr_B}{a_0}})= \\ \dfrac{1}{2\pi(1 - S)}(\dfrac{Z}{a_0})^{3}(e^{-\dfrac{2Zr_A}{a_0}}+e^{-\dfrac{2Zr_A}{a_0}}-2e^{-\dfrac{Zr_A}{a_0}-\dfrac{Zr_A}{a_0}})= \\ \dfrac{1}{2\pi(1 - S)}(\dfrac{Z}{a_0})^{3}(2e^{-\dfrac{2Zr_A}{a_0}}-2e^{-\dfrac{2Zr_A}{a_0}})=0 \ (4 \ points) \ \]

Q9.

Estimate the ground-state energy of a harmonic oscillator using the following trial wavelfunction. Compare your answer to the energy of the true harmonic oscillator solution.

\[\psi=\alpha^2-x^2, \ where \ |x|<\alpha, \ and \ \psi=0, \ where \ |x|>\alpha\]

According to variational method the expression for the upper bound of the ground state energy is

\[\dfrac{\left \langle \psi | H | \psi \right \rangle}{\left \langle \psi | \psi \right \rangle} \]

Normalization

\[\left \langle \psi | \psi \right \rangle = \int_{-\alpha}^{\alpha}(\alpha^2-x^2)^2 dx=\int_{-\alpha}^{\alpha}(\alpha^4-2\alpha^2x^2+x^4)dx= \\(\dfrac{x^5}{5}-2\alpha^2\dfrac{x^3}{3}+\alpha^4x)\Biggr\rvert_{-\alpha}^{\alpha}=(\dfrac{\alpha^5}{5}-2\alpha^2\dfrac{\alpha^3}{3}+\alpha^4\alpha)-(\dfrac{(-\alpha)^5}{5}-2\alpha^2\dfrac{(-\alpha)^3}{3}+\alpha^4(-\alpha))= \\ \dfrac{\alpha^5}{5}-2\dfrac{\alpha^5}{3}+\alpha^5+\dfrac{\alpha^5}{5}-2\dfrac{\alpha^5}{3}+\alpha^5=\dfrac{2\alpha^5}{5}-4\dfrac{\alpha^5}{3}+2\alpha^5=\alpha^5 \dfrac{6-20+30}{15}=\dfrac{16}{15}\alpha^5 \tag{5 points} \]

Numerator

\[\left \langle \psi | H | \psi \right \rangle=\int_{-\alpha}^{\alpha}(\alpha^2-x^2)(-\dfrac{\hbar^2}{2m}\dfrac{d^2}{dx^2}+\dfrac{1}{2}kx^2)(\alpha^2-x^2)dx = \\ \int_{-\alpha}^{\alpha}(\alpha^2-x^2)(-\dfrac{\hbar^2}{2m}\dfrac{d^2}{dx^2})(\alpha^2-x^2)dx+\int_{-\alpha}^{\alpha}(\alpha^2-x^2)\dfrac{1}{2}kx^2(\alpha^2-x^2)dx=I_1+I_2\]

Calculation of \(I_1\)

\[I_1=\int_{-\alpha}^{\alpha}(\alpha^2-x^2)(-\dfrac{\hbar^2}{2m}\dfrac{d^2}{dx^2})(\alpha^2-x^2)dx=\int_{-\alpha}^{\alpha}(\alpha^2-x^2)(-\dfrac{\hbar^2}{2m}\dfrac{d}{dx})(-2x)dx = \\ \int_{-\alpha}^{\alpha}(\alpha^2-x^2)(-\dfrac{\hbar^2}{2m})(-2)dx=\dfrac{\hbar^2}{m}\int_{-\alpha}^{\alpha}(\alpha^2-x^2)dx= \\ \dfrac{\hbar^2}{m}(\alpha^2x-\dfrac{x^3}{3})\Biggr\rvert_{-\alpha}^{\alpha}=\dfrac{\hbar^2}{m}((\alpha^2\alpha-\dfrac{\alpha^3}{3})-(\alpha^2(-\alpha)-\dfrac{(-\alpha)^3}{3}))=\dfrac{\hbar^2}{m}(2\alpha^3-\dfrac{2\alpha^3}{3})=\dfrac{\hbar^2}{m}\dfrac{(6-2)\alpha^3}{3}=\dfrac{4\hbar^2\alpha^3}{3m} \tag{4 points} \]

Calculation of \(I_2\)

\[I_2=\int_{-\alpha}^{\alpha}(\alpha^2-x^2)\dfrac{1}{2}kx^2(\alpha^2-x^2)dx=\int_{-\alpha}^{\alpha}(\alpha^2-x^2)^2\dfrac{1}{2}kx^2dx=\int_{-\alpha}^{\alpha}(\alpha^4-2\alpha^2x^2+x^4)\dfrac{1}{2}kx^2dx= \\ \dfrac{1}{2}k \int_{-\alpha}^{\alpha}(\alpha^4x^2-2\alpha^2x^4+x^6)dx=\dfrac{1}{2}k (\alpha^4\dfrac{x^3}{3}-2\alpha^2\dfrac{x^5}{5}+\dfrac{x^7}{7})\Biggr\rvert_{-\alpha}^{\alpha} = \\ \dfrac{1}{2}k (\dfrac{2\alpha^7}{3}-4\dfrac{\alpha^7}{5}+2\dfrac{\alpha^7}{7})=\dfrac{1}{2}k\dfrac{2(35-42+15)\alpha^7}{105}=\dfrac{8k\alpha^7}{105} \tag{4 points} \]

Addition of \(I_1\) and \(I_2\) and division by normalization constant gives

\[E(\alpha)=\dfrac{\left \langle \psi | H | \psi \right \rangle}{\left \langle \psi | \psi \right \rangle}=\dfrac{5\hbar^2}{4m\alpha^2}+\dfrac{k\alpha^2}{14} \tag{2 points} \]

Minimization

\[\dfrac{dE(\alpha)}{d\alpha}=\dfrac{-5\hbar^2}{2m\alpha^3}+\dfrac{k\alpha}{7}=0 \]

Remember the expression for \(k\):

\(\omega=\sqrt{\dfrac{k}{m}}\), \(\omega^2=\dfrac{k}{m}\), thus \(k=m\omega^2\), then

\[\dfrac{dE(\alpha)}{d\alpha}=\dfrac{-5\hbar^2}{2m\alpha^3}+\dfrac{k\alpha}{7}=\dfrac{-5\hbar^2}{2m\alpha^3}+\dfrac{m\omega^2\alpha}{7} \tag{4 points} \]

Parameter value that minimizes \(E(\alpha)\) is

\[\alpha_{min}^2=\sqrt{\dfrac{35}{2}}\dfrac{\hbar}{m\omega} \tag{3 points} \]

The final expression for the upper bound of the ground-state energy is

\[E(\alpha_{min})=\dfrac{5}{4}\sqrt{\dfrac{2}{35}}\hbar\omega+\dfrac{1}{14}\sqrt{\dfrac{35}{2}}\hbar\omega \tag{3 points} \]

The true energy for the ground state of harmonic oscillator is \(\dfrac{\hbar\omega}{2}\) whereas the estimate appeared to be ≈ \(0.598\hbar\omega\). The estimate is \(\dfrac{0.598 \hbar \omega - 0.5 \hbar \omega}{0.5 \hbar \omega} = 0.2 \) or 20% greater than the true energy (5 points).