2015 Exam 2 Solutions

Q1.

The energy of a rigid rotor is found by:

\[E=BJ(J+1) \tag{1} \]

We need to find \(B\) from the given mass and bond length.

\[B = \dfrac{\hbar^2}{2I} = \dfrac{\hbar^2}{2{\mu}r^2} \tag{2}\]

\[\mu = \dfrac{m_H \times m_H}{m_H + m_H} = \dfrac{m_H}{2} \tag{3} \]

Therefore

\[I = \mu r^2 = 4.65 \times 10^{-48} \;kg \,m^2 \tag{4}\]

Putting these all together we have

\[E = \dfrac{\hbar^2J(J+1)}{m_Hr^2} = \dfrac{(1.05 \times 10^{-34} \;J)^2 1(1+1)}{(1.67 \times 10^{-27} \; kg)(74.6 \times 10^{-12} m)^2} \tag{5}\]

\[E = 2.37 \times 10^{-21} J \tag{6}\]

Q2.

With no shielding the total energy is the same as the Hydrogen atom.

\[E = -13.6 \; eV \dfrac{Z^2}{n^2} \tag{7}\]

\[E = -13.6 \; eV \dfrac{Z^2}{n^2} = -13.6 \; eV \dfrac{3^2}{2^2} =30.6 \; eV \tag{7}\]

With shielding we find the \(Z_{eff}\) with the ionization energy as the total energy value.

\[E = -13.6 \; eV \dfrac{Z_{eff}^2}{n^2} = -5.39 \; eV \tag{8} \]

\[Z_{eff} = \sqrt{\dfrac {-5.39 \;eV \times 2^2}{-13.6 \; eV}} \tag{9} \]

\[Z_{eff} = 1.26 \tag{10}\]

Q3.

The probability of finding an electron at a radius \(\r) from the nucleus depends on the wavefunction and is determined by

\[Prob = 4\pi r^2R(r)^2 dr \tag{11} \]

Graphically for the 1s and 2s orbitals we have

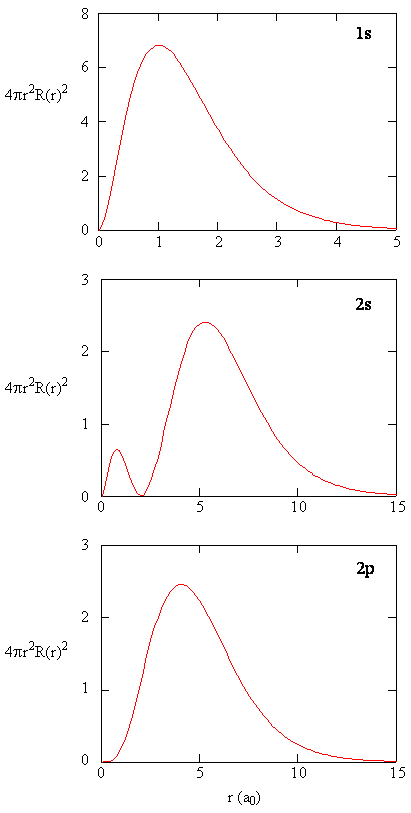
The probability of finding the election at \(r= 0\) in either orbital is \(0\)

Q4.

The expectation value of \(r\) in the 1s state of H is determined by

\[\langle \psi|r|\psi \rangle = \langle Y_{m,l} R_r|r|Y_{m,l} R_r \rangle \tag{12}\]

\[\int_0^\infty \int_0^\pi \int_0^{2\pi} \dfrac {1}{\sqrt{\pi}} \left(\frac{Z}{a_0}\right)^{\frac{3}{2}} e^{\frac{-Zr}{a_0}} \times r \times \dfrac {1}{\sqrt{\pi}} \left(\dfrac{Z}{a_0}\right)^{\frac{3}{2}} e^{\frac{-Zr}{a_0}} \underbrace{r^2 \sin\theta}_{Jacobian} \,dr\, d\theta\, d\phi \tag{13}\]

\[ \dfrac{1}{\pi} \left(\dfrac{Z}{a_0}\right)^{3} \int_0^\infty r^3 e^{\dfrac{-2Zr}{a_0}} dr \int_0^\pi \sin\theta \,d\theta \int_0^{2\pi} d\phi \tag{14}\]

The angular part of the integral is equal to \(4\pi\)

\[ \dfrac{4Z^3}{a_0^3} \int_0^\infty r^3 e^{\dfrac{-2Zr}{a_0}} dr \tag{15}\]

\[ \dfrac{4Z^3}{a_0^3} \dfrac{3!a_0^4}{2^4Z^4} \tag{16}\]

\[ \langle r \rangle = \dfrac {3a_0}{2Z} = \dfrac {3a_0}{2} \tag{17} \]

for H as \(Z = 1\)

Q5

There is two possible ways to solve the problem.

1. To apply both operators \(L_z\) and \(L^2\) on the wavefunction in the question and find eigenvalues \(m\) and \(l\).
2. To apply one of the operators \(L_z\) or \(L^2\) on the wavefunction in the question, and find eigenvalue \(m\) or \(l\), and show that these operators have the same eigenstates set (or \([L_z,L^2]=0\)).

For the solution you need to remember the expressions for \(L_z\) and \(L^2\) operators:

In Cartesian Coordinates

• \(\hat L_x=\hat y\hat p_z-\hat z\hat p_y=-i\hbar \left(y\dfrac{\partial }{\partial z}-z\dfrac{\partial}{\partial y}\right)\)
• \(\hat L_y=\hat z\hat p_x-\hat x\hat p_z=-i\hbar \left(z\dfrac{\partial }{\partial x}-x\dfrac{\partial}{\partial z}\right)\)
• \(\hat L_z=\hat x\hat p_y-\hat y\hat p_x=-i\hbar \left(x\dfrac{\partial }{\partial y}-y\dfrac{\partial}{\partial x}\right)\)

• \(\hat L^2=\hat L_x^2+\hat L_y^2+\hat L_z^2 = \hat L_x \hat L_x+\hat L_y \hat L_y+\hat L_z \hat L_z =\\ -\hbar^2((y^2+z^2)\dfrac{\partial^2}{\partial x^2} + (x^2+z^2)\dfrac{\partial^2}{\partial y^2} + (y^2+x^2)\dfrac{\partial^2}{\partial z^2}-2 (xy\dfrac{\partial^2}{\partial x \partial y}+xz\dfrac{\partial^2}{\partial x \partial z}+zy\dfrac{\partial^2}{\partial z \partial y})-2(x \dfrac{\partial }{\partial x}+y \dfrac{\partial }{\partial y}+z \dfrac{\partial }{\partial z}))\)

In Spherical Coordinates

• \(L_x = {\rm i}\,\hbar\,\left(\sin\varphi\, \dfrac{\partial}{\partial \theta} + \cot\theta \cos\varphi\,\dfrac{\partial}{\partial \varphi}\right) \)
• \( L_y = -{\rm i} \,\hbar\,\left(\cos\varphi\, \dfrac{\partial}{\partial\theta} -\cot\theta \sin\varphi \,\dfrac{\partial}{\partial \varphi}\right)\)
• \(L_z = -{\rm i}\,\hbar\,\dfrac{\partial}{\partial\varphi}\)
• \(L^2 = - \hbar^2\left( \dfrac{1}{\sin\theta}\dfrac{\partial}{\partial \theta} \sin \theta \dfrac{\partial}{\partial \theta} + \dfrac{1}{\sin^2\theta}\dfrac{\partial^2} {\partial\varphi^2}\right)\)

Cartesian coordinates:

Calculation of \(L_z\) in Cartesian coordinates:

\[\hat L_z (x^2+y^2-2z^2)=\hat x\hat p_y-\hat y\hat p_x (x^2+y^2-2z^2)= \\ -i\hbar \left(x\dfrac{\partial }{\partial y}-y\dfrac{\partial}{\partial x}\right) (x^2+y^2-2z^2) = \\ -i\hbar (x2y-y2x)=0\]

Thus, \(m\hbar=0\) and \(m=0\).

Calculation of \(L^2\) starts with calculation of the squares of its angular momentum components \(\hat L_x \hat L_x\),\(\hat L_y \hat L_y\) and \(\hat L_z \hat L_z\):

\[\hat L_x(\hat L_x (x^2+y^2-2z^2))=\\ (\hat y\hat p_z-\hat z\hat p_y)(\hat y\hat p_z-\hat z\hat p_y)(x^2+y^2-2z^2)=\\ -\hbar^2 \left(y\dfrac{\partial }{\partial z}-z\dfrac{\partial}{\partial y}\right)\left(y\dfrac{\partial }{\partial z}-z\dfrac{\partial}{\partial y}\right)(x^2+y^2-2z^2)= \\ -\hbar^2\left(y\dfrac{\partial }{\partial z}-z\dfrac{\partial}{\partial y}\right)(y(-4z)-z(2y))= \\ -\hbar^2 \left(y\dfrac{\partial }{\partial z}-z\dfrac{\partial}{\partial y}\right)(-6yz)= \\ -\hbar^2 (y(-6y)-z(-6z))=6\hbar^2 (y^2-z^2)\]

\[\hat L_y(\hat L_y (x^2+y^2-2z^2))= \\ (\hat z\hat p_x-\hat x\hat p_z)(\hat z\hat p_x-\hat x\hat p_z)(x^2+y^2-2z^2)= \\ -i\hbar \left(z\dfrac{\partial }{\partial x}-x\dfrac{\partial}{\partial z}\right)(-i\hbar) \left(z\dfrac{\partial }{\partial x}-x\dfrac{\partial}{\partial z}\right)(x^2+y^2-2z^2)= \\ -\hbar^2\left(z\dfrac{\partial }{\partial x}-x\dfrac{\partial}{\partial z}\right)\left(z\dfrac{\partial }{\partial x}-x\dfrac{\partial}{\partial z}\right)(x^2+y^2-2z^2)= \\ -\hbar^2\left(z\dfrac{\partial }{\partial x}-x\dfrac{\partial}{\partial z}\right)(z(2x)-x(-4z))= \\ -\hbar^2\left(z\dfrac{\partial }{\partial x}-x\dfrac{\partial}{\partial z}\right)(6xz)= \\ -\hbar^2(z(6z)-x(6x))=-6\hbar^2(z^2-x^2)=6\hbar^2(x^2-z^2)\]

\[\hat L_z(\hat L_z (x^2+y^2-2z^2))=\hat L_z(0)=0\]

Final calculation of \(L^2\) in Cartesian coordinates:

\[\hat L^2=\hat L_x^2+\hat L_y^2+\hat L_z^2 = \hat L_x \hat L_x+\hat L_y \hat L_y+\hat L_z \hat L_z = \\ 6\hbar^2 (y^2-z^2)+6\hbar^2(x^2-z^2) = \\ 6\hbar^2 (x^2+y^2-2z^2)\]

Thus, \(l(l+1)\hbar^2 = 6\hbar^2\) and \(l=2\).

Spherical coordinates:

Calculation of \(L_z\) in spherical coordinates:

First we need to remember the transform of Cartesian to spherical coordinates:

\[x = r \,\sin\theta\, \cos\varphi \]

\[ y = r\, \sin\theta\, \sin\varphi \]

\[ z =r \cos \theta \]

Transform the wavefunction to spherical coordinates :

\[\psi=x^2+y^2-2z^2 = r ^2\,\sin^2\theta\, \cos^2\varphi + r^2\, \sin^2\theta\, \sin^2\varphi -2 r ^2\cos^2 \theta = \\ r ^2 \sin^2\theta (\cos^2\varphi + \sin^2\varphi) -2 r ^2\cos^2 \theta = r ^2 \sin^2\theta -2 r ^2\cos^2 \theta\]

\[L_z=-i\hbar \dfrac{\partial}{\partial \phi}(r ^2 \sin^2\theta -2 r ^2\cos^2 \theta) = 0\]

Thus, \(m\hbar=0\) and \(m=0\).

Calculation of \(L^2\) in spherical coordinates:

Plug the transformed wavefunction in the equation for \(L^2\):

\[L^2 = - \hbar^2\left( \dfrac{1}{\sin\theta}\dfrac{\partial}{\partial \theta} \sin \theta \dfrac{\partial}{\partial \theta} + \dfrac{1}{\sin^2\theta}\dfrac{\partial^2} {\partial\varphi^2}\right) ( r^2 \sin^2 \theta -2 r^2\cos^2 \theta) =\\ - \hbar^2 \dfrac{1}{\sin\theta}\dfrac{\partial}{\partial \theta} (\sin \theta (2 \sin \theta \cos \theta - 4 \cos \theta (-\sin \theta))= \\ - \hbar^2 \dfrac{1}{\sin\theta}\dfrac{\partial}{\partial \theta} (2\sin^2 \theta \cos \theta +4\cos \theta \sin^2 \theta)= \\ - \hbar^2\dfrac{1}{\sin\theta}(4 \sin \theta \cos^2 \theta +2 \sin^2 \theta (-\sin \theta)+4\cos\theta 2\sin \theta \cos \theta + 4 \sin^2 \theta (-\sin \theta)) = \\ - \hbar^2 \dfrac{1}{\sin\theta} ( 4 \sin \theta \cos^2 \theta - 2 \sin^3 \theta +8\sin \theta \cos \theta - 4\sin^3 \theta) = \\ - \hbar^2 \dfrac{1}{\sin\theta} (12 \sin \theta \cos^2 \theta - 6 \sin^3 \theta) = - \hbar^2 (12 \cos^2 \theta - 6 \sin^2 \theta) = \hbar^2 (6 \sin^2 \theta - 12 \cos^2 \theta) = 6 \hbar^2 (\sin^2 \theta - 2 \cos^2 \theta)\]

Thus, \(l(l+1)\hbar^2 = 6 \hbar^2\) and \(l=2\).

Q6.

\[ | \psi_{trial} \rangle = Ne^{-\beta x^2}\]

\[E_{trial}= \dfrac{\langle\psi_{trial}| H | \psi_{trial}\rangle}{\langle\psi_{trial} | \psi_{trial} \rangle}\]

\[H = \dfrac{-\hbar^2}{2m} \dfrac{\delta^2}{\delta x^2}\]

\[\langle\psi_{trial}|\psi_{trial}\rangle = \int_{-\infty}^{\infty} N^2 e^{-2\beta x^2} dx = N^2(\dfrac{\pi}{2\beta})^{\dfrac{1}{2}} = 1\]

\[N = (\dfrac{\pi}{2\beta})^{\dfrac{-1}{4}}\]

\[E_{trial} = {\langle\psi_{trial}| H | \psi_{trial}\rangle} = \int_{-\infty}^{\infty} N^2 e^{-\beta x^2} \dfrac{-\hbar}{2m} \dfrac{\delta^2}{\delta x^2} e^{-\beta x^2} dx = \int_{-\infty}^{\infty} N^2 e^{-\beta x^2} \dfrac{-\hbar}{2m} \dfrac{\delta}{\delta x} (-2x\beta) e^{-\beta x^2} dx\]

\[= \int_{-\infty}^{\infty} N^2 e^{-\beta x^2} \dfrac{-\hbar}{2m} (-2\beta e^{-\beta x^2} + 4x^2\beta^2 e^{-\beta x^2})dx\]

\[= \dfrac{-N^2 \hbar^2}{2m} \int_{-\infty}^{\infty} e^{-\beta x^2}(-2\beta e^{-\beta x^2} + 4x^2\beta^2 e^{-\beta x^2})dx = \dfrac{-N^2 \hbar^2}{2m} (\int_{-\infty}^{\infty}-2\beta e^{-2\beta x^2} dx + \int_{-\infty}^{\infty} 4x^2\beta^2 e^{-2\beta x^2}dx)\]

\[=\dfrac{-N^2 \hbar^2}{2m} (-2\beta ((\dfrac{\pi}{2\beta})^{\dfrac{1}{2}} + (4\beta^2)(\dfrac{1}{4\beta}(\dfrac{\pi}{2\beta})^{\dfrac{1}{2}})\]

\[= \dfrac{-2(\dfrac{\pi}{2\beta})^{\dfrac{-1}{2}} \hbar^2}{2m}(-2\beta (\dfrac{\pi}{2\beta})^{\dfrac{1}{2}} + \beta (\dfrac{\pi}{2\beta})^{\dfrac{1}{2}}\]

\[= \dfrac{-2\hbar^2}{2m} (-2\beta + \beta) = \dfrac{\beta \hbar^2}{m} = E_{trial}\]

\[\dfrac{dE_{trial}}{d\beta} = \dfrac{\hbar^2}{m}\]

As beta is not in this derivative there is no way to minimize it using this method. Looking at the equation for the trial energy though it can be clearly seen that it minimizes at \(\beta = 0\). This value of zero arises because of the limits of integration that were used in order to calculate the integrals, we had to extend L out to infinity and zero to minus infinity so instead of having a particle in a box, we have a free particle which has no zero point energy. So if you did the problem this way, correctly you received full credit. The following is the more correct way solve the problem.

\[E_{trial}= \dfrac{\langle\psi_{trial}| H | \psi_{trial}\rangle}{\langle\psi_{trial} | \psi_{trial} \rangle}\]

\[H = \dfrac{-\hbar^2}{2m} \dfrac{\delta^2}{\delta x^2}\]

\[\langle\psi_{trial}|\psi_{trial}\rangle = \int_{0}^{L} N^2 e^{-2\beta x^2} dx = \int_{-(2\beta)^{1/2}L/2}^{(2\beta)^{1/2}L/2} N^2 (2\beta)^{1/2}e^{-t^2}dt = 1\]

Where \(t = (2\beta)^{1/2} x\) and \(dt = (\beta)^{1/2} dx\)

\[N = (\beta \pi)^{-1/4} \times (erf((2\beta)^{1/2} L))^{-1/2}\]

Where \(erf((2\beta)^{1/2}L\) is the error function evaluated at \((2\beta)^{1/2}L\).

\[ E_{trial} = {\langle\psi_{trial}| H | \psi_{trial}\rangle} = \int_{-(2\beta)^{1/2}L/2}^{(2\beta)^{1/2}L/2} N^2 e^{-\beta x^2} \dfrac{-\hbar}{2m} \dfrac{\delta^2}{\delta x^2} e^{-\beta x^2} dx = \int_{-(2\beta)^{1/2}L/2}^{(2\beta)^{1/2}L/2} N^2 e^{-\beta x^2} \dfrac{-\hbar}{2m} \dfrac{\delta}{\delta x} (-2x\beta) e^{-\beta x^2} dx\]

\[ = \int_{-(2\beta)^{1/2}L/2}^{(2\beta)^{1/2}L/2} N^2 \beta^{-1/2}e^{-t^2} \dfrac{-\hbar}{2m} (-2\beta e^{-t^2} + 4t^2\beta e^{-t^2})dt\]

\[= -\frac{N^2 \hbar^2}{2m\beta^{1/2}}[(-2\beta \int_{-(2\beta)^{1/2}L/2}^{(2\beta)^{1/2}L/2}e^{-t^2}dt) + (2\beta \int_{-(2\beta)^{1/2}L/2}^{(2\beta)^{1/2}L/2}t^2e^-t^2 dt)]\]

\[= -\frac{N^2 \hbar^2 \beta^{1/2}}{2m}(\frac{L(2\beta)^{1/2}}{2e^{L^22\beta}} - \frac{1}{2}\pi^{1/2}ierfi(\frac{Li(2\beta)^{1/2}}{2})\]

Where erfi is the imaginary error function. So overall we have for the unoptimized ground state energy:

\[E_{trial} = -\frac{(\beta \pi)^{-1/2} \times (erf((2\beta)^{1/2} L))^{-1} \hbar^2 \beta^{1/2}}{2m}(-\frac{L(2\beta)^{1/2}}{2e^{L^22\beta}} + \frac{1}{2}\pi^{1/2}erf(\frac{-L(2\beta)^{1/2}}{2}))\]

Normally to optimize the energy we would take the derivative of our trial energy with respected to beta and find the minimum. Here due to the complexity of the equation an easier solution would be to numerically plot the energy as a function of beta, though to do that we would need to have a value for L.