Solutions 8

Q7.10

In this problem the perturbation to the Hamiltonian is in the potential term. That's good because we don't need to take any derivatives.

\[\hat{H}=-\dfrac{(\hbar)^2}{2m}\dfrac{d}{dx^2}+\dfrac{1}{2}kx^2 + ax^3 \tag{1}\]

\[\hat{H}^1=ax^3 \tag{2}\]

\[E^1 = <\psi_0|\hat{H}^1|\psi_0> \tag{3}\]

\[E^1 = <\psi_0|ax^3|\psi_0> \tag{4}\]

Looking at the graph of the Harmonic Oscillator wavefunctions we see that \(\psi_0\) is even.

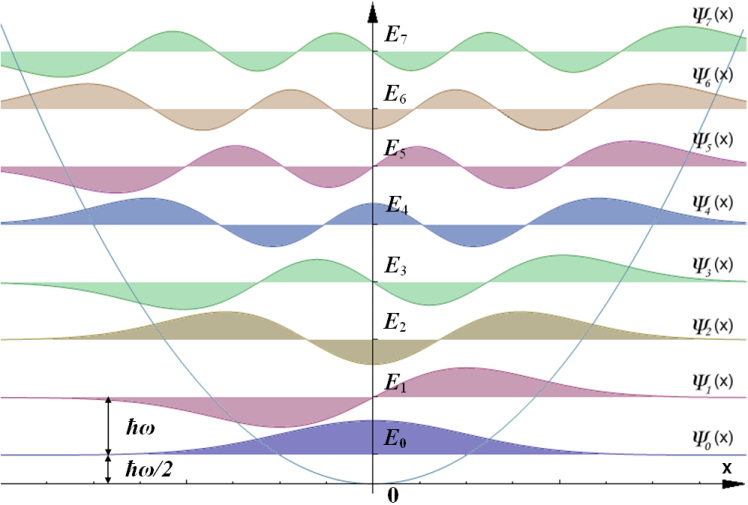
Image used with permission from Wikipedia.

\[E^1 = <\psi_0|ax^3|\psi_0> = <even|odd|even> = <odd> = 0 \tag{5}\]

Q7.11

Now we add another term to the potential.

\[\hat{H}=-\dfrac{(\hbar)^2}{2m}\dfrac{d}{dx^2}+\dfrac{1}{2}kx^2 + ax^3 +ax^4 \tag{6}\]

\[\hat{H}^1=ax^3 + ax^4 \tag{7}\]

\[E^1 = \langle\psi_0|\hat{H}^1|\psi_0\rangle \tag{8}\]

\[E^1 = \langle\psi_0|ax^3 + ax^4|\psi_0\rangle = \langle\psi_0|ax^3|\psi_0\rangle + \langle\psi_0|ax^4|\psi_0\rangle\tag{9}\]

\[E^1 = 0 + \langle\psi_0|ax^4|\psi_0\rangle\tag{10}\]

\[E^1 = \langle\psi_0|ax^4|\psi_0\rangle = \int_{-\infty}^{\infty} (\dfrac{\alpha}{\pi})^{1/4}e^{-\alpha x^2 / 2} \times ax^4 \times (\dfrac{\alpha}{\pi})^{1/4}e^{-\alpha x^2 / 2} dx \tag{11}\]

\[E^1 = a (\dfrac{\alpha}{\pi})^{1/2} \int_{-\infty}^{\infty} x^4 e^{-\alpha x^2} dx = constants\int_{-\infty}^{\infty} even \tag{12}\]

\[E^1 = 2a (\dfrac{\alpha}{\pi})^{1/2} \int_{0}^{\infty} x^4 e^{-\alpha x^2} dx \tag{13}\]

\[E^1 = 2a (\dfrac{\alpha}{\pi})^{1/2} \dfrac{3}{8\alpha^2}(\dfrac{\pi}{\alpha})^{1/2} \tag{14}\]

\[E^1 = \dfrac{3a}{4\alpha^2} \tag{15}\]

Q7.12

To find the wavefunction we have to do an infinite number of integrals.... But many of them are equal to \(0\) or so small that we can ignore them.

\[ | n \rangle = | n^o \rangle + | n^1 \rangle = | n^o \rangle + \sum _{m \neq n} \dfrac{|m^o \rangle \langle m^o | \hat{H}^1| n^o \rangle }{E_n^o - E_m^o} \tag{16}\]

\[\hat{H}^1=ax^3 \tag{2}\]

Look at the infinite sum, when do the integrals go to zero?

\[\langle \psi_{m^o}|ax^3|\psi_{n^o}\rangle = \langle even|odd|even\rangle or \langle odd|odd|odd\rangle = \langle odd\rangle = 0 \tag{17} \]

Therefore

\[\langle \psi_0|ax^3|\psi_2\rangle = \langle \psi_0|ax^3|\psi_4\rangle = \langle \psi_2|ax^3|\psi_4\rangle = \langle \psi_1|ax^3|\psi_3\rangle = etc etc = 0 \tag{18} \]

So many of our integrals are zero.

Now look at the denominator

\[E_n^o - E_m^o \tag {19}\]

is large when there are two very different wavefunctions and will make the sum term small enough to ignore.

What's left?

\[ | n \rangle = | \psi_0^0 \rangle + | \psi_0^1 \rangle = | \psi_0 \rangle + \dfrac{|\psi_1 \rangle \langle \psi_1 | \hat{H}^1| \psi_0 \rangle }{E_0^o - E_1^o} + \dfrac{|\psi_ 3\rangle \langle \psi_3 | \hat{H}^1| \psi_0 \rangle }{E_0^o - E_3^o} + \dfrac{|\psi_ 5\rangle \langle \psi_5 | \hat{H}^1| \psi_0 \rangle }{E_0^o - E_5^o} \tag{20}\]

Fix here with alphas

One term at a time

\[\dfrac{|\psi_1 \rangle \langle \psi_1 | \hat{H}^1| \psi_0 \rangle }{E_0^o - E_1^o} = \dfrac{|(\dfrac{4a ^3}{\pi})^{1/4}xe^{-\alpha x^2 /2} \rangle \langle (\dfrac{4a ^3}{\pi})^{1/4}xe^{-a x^2 /2} \times ax^3 \times (\dfrac{a}{\pi})^{1/4}e^{-a x^2 / 2} \rangle }{1/2 h \nu - 3/2 h \nu}\tag{21}\]

After integration and much simplification which I'm not going to type out the first term is

\[\dfrac{|\psi_1 \rangle \langle \psi_1 | \hat{H}^1| \psi_0 \rangle }{E_0^o - E_1^o} = \dfrac{-6}{h\nu} (\dfrac{a}{\pi})^{1/4}x e^{ax^2/2} \tag{22}\]

The second term

\[\dfrac{|\psi_3 \rangle \langle \psi_3 | \hat{H}^1| \psi_0 \rangle }{E_0^o - E_3^o} = \dfrac{|(\dfrac{a ^3}{9\pi})^{1/4}(2ax^3 -3x) e^{-\alpha x^2 /2} \rangle \langle (\dfrac{a ^3}{9\pi})^{1/4}(2ax^3 -3x) e^{-\alpha x^2 /2} \times ax^3 \times (\dfrac{a}{\pi})^{1/4}e^{-a x^2 / 2} \rangle }{1/2 h \nu - 5/2 h \nu}\tag{23}\]

Some combination of constants and seperation into 2 integrals gives

\[\dfrac{|\psi_3 \rangle \langle \psi_3 | \hat{H}^1| \psi_0 \rangle }{E_0^o - E_3^o} = \dfrac{(\dfrac{a ^3}{9\pi})^{1/4}(2ax^3 -3x) e^{-a x^2 /2} \left[ \dfrac{4a^3}{9^{1/4}\pi^{1/2}} \int_0^\infty x^6 e^{-ax^2} dx - \dfrac{6a^2}{9^{1/4}\pi^{1/2}} \int_0^\infty x^4 e^{ax^2} dx \right] }{1/2 h \nu - 5/2 h \nu}\tag{24}\]

\[\dfrac{|\psi_3 \rangle \langle \psi_3 | \hat{H}^1| \psi_0 \rangle }{E_0^o - E_3^o} =\dfrac{-1}{4h\nu}(\dfrac{a}{\pi})^{1/4}(2ax^3 - 3x) e^{-a x^2 /2}\tag{25}\]

I'm going to assume that

\[\dfrac{|\psi_5 \rangle \langle \psi_5 | \hat{H}^1| \psi_0 \rangle }{E_0^o - E_5^o} = 0 \tag{26}\]

Cause that integral is HARD and th energy difference is bigger.

Therefore the final answer is:

\[ | n \rangle = (\dfrac{a}{\pi})^{1/4}e^{-a x^2 / 2} + \dfrac{-6}{h\nu} (\dfrac{a}{\pi})^{1/4} e^{ax^2/2} + \dfrac{-1}{4h\nu}(\dfrac{a}{\pi})^{1/4}(2ax^3 - 3x) e^{-a x^2 /2} \]

\[= |\psi_0\rangle +\dfrac{-6}{4^{1/4}a^{1/2}h\nu} |\psi_1\rangle + \dfrac{-9^{1/4}}{a^{1/2}4h\nu} |\psi_3\rangle \]

\[= |\psi_0\rangle +\dfrac{-4.28}{a^{1/2}h\nu} |\psi_1\rangle + \dfrac{-0.433}{a^{1/2}h\nu} |\psi_3\rangle \tag{27}\]

Q7.13 (VERY optional)

\[E_{trial}= \dfrac{\langle\psi_{trial}| H | \psi_{trial}\rangle}{\langle\psi_{trial} | \psi_{trial} \rangle}\]

\[H = \dfrac{-\hbar^2}{2m} \dfrac{\delta^2}{\delta x^2}\]

\[\langle\psi_{trial}|\psi_{trial}\rangle = \int_{0}^{L} N^2 e^{-2\beta x^2} dx = \int_{-(2\beta)^{1/2}L/2}^{(2\beta)^{1/2}L/2} N^2 (2\beta)^{1/2}e^{-t^2}dt = 1\]

where

• \(t = (2\beta)^{1/2} x\) and
• \(dt = (\beta)^{1/2} dx\)

\[N = (\beta \pi)^{-1/4} \times (erf((2\beta)^{1/2} L))^{-1/2}\]

Where \(erf((2\beta)^{1/2}L\) is the error function evaluated at \((2\beta)^{1/2}L\).

\[ E_{trial} = {\langle\psi_{trial}| H | \psi_{trial}\rangle} = \int_{-(2\beta)^{1/2}L/2}^{(2\beta)^{1/2}L/2} N^2 e^{-\beta x^2} \dfrac{-\hbar}{2m} \dfrac{\delta^2}{\delta x^2} e^{-\beta x^2} dx = \int_{-(2\beta)^{1/2}L/2}^{(2\beta)^{1/2}L/2} N^2 e^{-\beta x^2} \dfrac{-\hbar}{2m} \dfrac{\delta}{\delta x} 2x\beta e^{-\beta x^2} dx\]

\[ = \int_{-(2\beta)^{1/2}L/2}^{(2\beta)^{1/2}L/2} N^2 \beta^{-1/2}e^{-t^2} \dfrac{-\hbar}{2m} (-2\beta e^{-t^2} + 4t^2\beta e^{-t^2})dt\]

\[= -\frac{N^2 \hbar^2}{2m\beta^{1/2}}\left[\left(-2\beta \int_{-(2\beta)^{1/2}L/2}^{(2\beta)^{1/2}L/2}e^{-t^2}dt\right) + \left(2\beta \int_{-(2\beta)^{1/2}L/2}^{(2\beta)^{1/2}L/2}t^2e^-t^2 dt\right)\right]\]

\[= -\frac{N^2 \hbar^2 \beta^{1/2}}{2m}(\frac{L(2\beta)^{1/2}}{2e^{L^22\beta}} - \frac{1}{2}\pi^{1/2}ierfi(\frac{Li(2\beta)^{1/2}}{2}) -(2\beta \pi)^{1/2}erf(\frac{(2\beta)^{1/2}L}{2})))\]

Where erfi is the imaginary error function. So overall we have for the unoptimized ground state energy:

\[E_{trial} = -\frac{(\beta \pi)^{-1/2} \times (erf((2\beta)^{1/2} \frac{L}{2}))^{-1} \hbar^2 \beta^{1/2}}{2m}(-\frac{L(2\beta)^{1/2}}{2e^{\frac{L^2\beta}{2}}} + \frac{1}{2}\pi^{1/2}erf(\frac{-L(2\beta)^{1/2}}{2}) - (2\beta \pi)^{1/2}erf(\frac{(2\beta)^{1/2}L}{2}))\]

Normally to optimize the energy we would take the derivative of our trial energy with respected to beta and find the minimum. Here due to the complexity of the equation an easier solution would be to numerically plot the energy as a function of beta, though to do that we would need to have a value for L.

A) and B) A Gaussian is a poor trial function for a particle in a box since a Gaussian does not go to zero at any values other than infinity. While the box potential has a finite size, if the box potential had infinite size then we would be dealing with a free particle.

C) This problem can be solved up to the unoptimized trial energy analytically but taking the derivative leads to a transcendental equation so it has to be solved numerically.