#5 Solutions

Q1

First from the many assignments before we should know by now that:

\[\sigma_x^2 = <x^2> - <x>^2 \tag{1}\]

And in any harmonic oscillator wavefunction \( <x> = 0 \) as the system is symmetric about the center of the distribution.

So all we have to find is \(<x^2>\) for \(\psi_0 \) and \(\psi_1\).

\[\psi_0 = \Big(\frac{\alpha}{\pi}\Big)^{1/4}e^{-(\alpha x^2)/2}\tag{2}\]

\[<x^2> = \Big(\frac{\alpha}{\pi}\Big)^{1/2}\int_{-\infty}^{\infty}x^2e^{-\alpha x^2} dx\tag{3}\]

You did this on your test....

\[\langle x^2 \rangle = 2 \Big(\dfrac{\alpha}{\pi}\Big) ^{1/2} \int_{0}^{\infty} x^2 e^{- \alpha x^2} dx \tag{4}\]

\[\langle x^2 \rangle = 2 \Big(\dfrac{\alpha}{\pi}\Big) ^{1/2} \times \dfrac{1}{2^2 \alpha} \Big(\dfrac{\pi}{\alpha}\Big) ^{1/2} \tag{5}\]

\[\langle x^2 \rangle = \dfrac{1}{2\alpha} \tag{6}\]

Then find the deviation

\[\sigma_x = \Big(\dfrac{1}{2\alpha}\Big)^{1/2} \tag{7} \]

And do the same for the first excited state.

\[\psi_1 = (\frac{4\alpha^3}{\pi})^{1/4}xe^{-(\alpha x^2)/2}\tag{8}\]

\[\langle x^2 \rangle = \Big(\frac{4\alpha^3}{\pi}\Big)^{1/2}\int_{-\infty}^{\infty} x^4e^{-(\alpha x^2)} \tag{9}\]

\[\langle x^2 \rangle = 2 \Big(\frac{4\alpha^3}{\pi}\Big)^{1/2} \int_{0}^{\infty} x^4e^{-(\alpha x^2)} \tag{10} \]

\[\langle x^2 \rangle = 2 \Big(\frac{4\alpha^3}{\pi}\Big)^{1/2} \dfrac{3}{2^3 \alpha^2} \Big(\dfrac{\pi}{\alpha}\Big)^{1/2} \tag{11}\]

\[\langle x^2 \rangle = \dfrac{3}{2 \alpha} \tag{12}\]

For \(\psi_1\)

\[\sigma_x = \Big(\dfrac{3}{2\alpha}\Big)^{1/2} \tag{13} \]

So the higher excited state has a larger deviation in x which means the wavefunction has a larger spread of the probability which is what you should expect from looking at the graphs.

Q2

Two requirements for a molecule to absorb IR radiation are that the normal coordinate motion of the molecule must cause it's dipole moment to change (1) and the energy level of the molecule (v) must change by plus or minus one (2).

Both of these are the result of the requirement that the transition moment integral be nonzero:

\[\int_a^b \psi_1 \hat\mu \psi_2 d\tau \tag{1} \]

Where \(\hat\mu\) is the dipole moment operator and \(\psi_1 , \psi_2 \) are the starting and ending wavefunctions.

Q3

To show that a transition is forbidden the transition moment integral must equal zero:

\[\psi_0 = (\frac{\alpha}{\pi})^{1/4}e^{-(\alpha x^2)/2}\ \tag{1}\]

\[\psi_2 = (\frac{\alpha}{4\pi})^{1/4}(2\alpha x^2 - 1)e^{-(\alpha x^2)/2}\tag{2}\]

\[\hat\mu = e_cx\tag{3}\]

This is \(e\) the charge on an electron not \(e\) the natural number so I added the subscript.

\[<\psi_0|<\hat\mu>|\psi_2> = e_c(\frac{\alpha^2}{4\pi^2})\int_{-\infty}^{\infty}(2\alpha x^3 - x)e^{-\alpha x^2} dx\tag{4}\]

This integral can be split up to two integrals \(\int_{-\infty}^{\infty}x^3e^{-\alpha x^2}dx\) and \(\int_{-\infty}^{\infty}xe^{-\alpha x^2}dx\) both of these integrals can be seen to be zero as they are odd functions integrated over symmetric limits. Thus the transition moment integral is zero and the transition is not possible.

\[\psi_1 = (\frac{4\alpha^3}{\pi})^{1/4}xe^{-(\alpha x^2)/2}\tag{5}\]

\[<\psi_0|<\hat\mu>|\psi_1> = e_c\int_{-\infty}^{\infty}(\frac{\alpha}{\pi})^{1/4}(\frac{4\alpha^3}{\pi})^{1/4}x^2e^{-\alpha x^2}dx = e(\frac{4\alpha^4}{\pi^2})^{1/2}(\frac{1}{2}(\frac{\pi}{\alpha^3})^{1/2}) = e_c(\frac{1}{2\alpha})^{1/2}\tag{6}\]

Since this integral is not zero the transition is allowed.

Q4

a) Not IR active

b) IR active

c) IR active

d) IR active

e) IR active

Q5

Overtones are transitions with \(\Delta v > 1\) which are forbidden in the harmonic oscillator model.

The presence of overtones in the IR spectrum reveals that the anharmonicity of the potential relaxes the selection rules imposed by the harmonic potential.

This figure compares the Harmonic Oscillator with anharmonic potential for diatomic molecules called the Morse Potential.

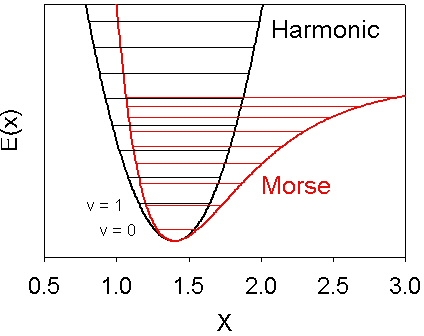
A few other things you should notice/know about the Morse and anharmonic potentials is the energy levels get closer as they get higher; the left or repulsive wall is steeper where the molecules come too close and repel each other; the right or attractive wall is shallower and flattens out at large distances to represent the energy of the seperated atoms.

There are other anharmonic potentials which share these features (Leonard-Jones) and all are still only models. Real molecules are HARD.

Q6

For each of these problems we need to use

\[E = h\nu \tag 1 \]

in the appropriate units.

\[c = \lambda\nu \tag 2\]

\[\nu = \dfrac{c}{\lambda} \tag 3 \]

UV- Vis, 500 nm

\[E = \dfrac{hc}{\lambda} = \dfrac{1.986\times 10^{-25} \;Jm}{500 \times 10^{-9} \;m} = 3.972 \times 10^{-19} \;J = 19995 \;cm^{-1} \tag 4\]

IR, 6 micron

\[E = \dfrac{hc}{\lambda} = \dfrac{1.986\times 10^{-25} \;Jm}{6 \times 10^{-6} \;m} = 3.31 \times 10^{-20} \;J = 1666 \;cm^{-1} \tag 5\]

Microwave, \(6 \times 10^{11} \;Hz\)

\[E = h\nu = (6.626 \times 10^{-34} \;Js)(6 \times 10^{11}) \;s^{-1} = 3.97 \times 10^{-22} \;J = 20.0\;cm^{-1} \tag 5\]

Q7

Spectroscopic Signature			Degree of Freedom
Type EM Range	Typical Wavelength of Transition	Typical Energy of Transition	sensitive to electronic transition (yes/no)	Sensitive to vibrational transition (yes/no)	sensitive to rotational transitions (yes/no)
UV-Visible	500 nm	\[4.0 \times 10^-19 \;J\] \[\approx 20,000 \; cm^{-1}\]	Y	Y, Vibrational fine structure is present in gas phase UV-Vis	N
Infrared	6 \(\mu\)	\[3.0 \times 10^-20 \;J\] \[\approx 2,000 \; cm^{-1}\]	N	Y	Y, Rotational fine structure is present in gas phase IR
Microwave	50 cm	\[3.0 \times 10^-22 \;J\] \[\approx 20 \; cm^{-1}\]	N	N	Y

If any spectroscopy is sensitive to more than one degree of freedom, explain why.

Q8

Energy of a rigid rotor is

\[E = BJ(J+1) \;where B = \dfrac{\hbar^2}{2I} \tag 1\]

for \(J = 5 \;and J = 20\)

\[E =\dfrac{J\hbar^2}{2I}(J+1) = \dfrac{5\hbar^2}{2I}(5+1) =\dfrac{30 \times (1.054 \times 10^{-34} \; Js)^2 }{2 \times 2.6 \times 10^{-47} \;Kg\times m^2} = 6.409 \times 10^{-20} J = 322 cm^{-1} \tag 2\]

\[E =\dfrac{J\hbar^2}{2I}(J+1) = \dfrac{20\hbar^2}{2I}(20+1) =\dfrac{420 \times (1.054 \times 10^{-34} \; Js)^2 }{2 \times 2.6 \times 10^{-47} \;Kg\times m^2} = 8.972 \times 10^{-20} J = 4516 cm^{-1} \tag 3\]

For the temperature

\[E=k_bT = E_{J=5} \tag4\]

\[T = \dfrac{E_{J=5}}{k_b} = \dfrac{322 cm^{-1}}{0.69 cm^{-1} \times K^{-1}} = 466 K \tag{5}\]

\[T = \dfrac{E_{J=20}}{k_b} = \dfrac{4516 cm^{-1}}{0.69 cm^{-1} \times K^{-1}} = 6544 K \tag{6}\]

Q9

The bond length is extra information you don't need. This problem is a plug and chug just like the last part of #8.

\[T = \dfrac{E_{v}}{k_b} = \dfrac{2886 cm^{-1}}{0.69 cm^{-1} \times K^{-1}} = 4182 K \tag{1}\]

Q10

a) Rotations are allowed to have J=0, so the zero point energy = 0. Vibrations have zero point energy and the value would be determined by the spring constant.

\[\omega = \sqrt{\dfrac{k}{\mu}} \tag{1}\]

\[\omega = \sqrt{\dfrac{970 \;N\times m^{-1}}{1.577 \times 10^{-27} \;kg}} = 7.84 \times 10^{14} \; Hz \tag{2}\]

\[E = (v +1/2)\hbar\omega = \dfrac{\hbar\omega}{2} = \dfrac{1.054 \times 10^{-34} \;Js \times 7.84 \times 10^{14} \; Hz}{2} = 4.13 \times 10^{-20} = 2080 \;cm^{-1} \tag{3}\]

b) The rotational transition will be from J=0 to J=1

\[E = BJ(J+1) \;Where B = \dfrac{\hbar^2}{2I} \;Where I = r^2\mu \tag {4}\]

\[E = \dfrac{2\hbar^2}{2r^2\mu} = \dfrac{2 \times (1.054 \times 10^{-34} \; Js) ^2}{2 \times (91.7 \times 10^{-12} \; m)^2 \times 1.577 \times 10^{-27} \; kg} = 8.377 \times 10^{-22} = 42 \;cm^{-1} \tag{5}\]