11.6: Properties of Liquids
- Page ID
- 42168
Introduction
Now that we have covered the basic Intermolecular Forces, we will cover some of the properties of liquids. These will include:
- Vaporization and Condensation
- Vapor Pressure
- Enthalpy of Vaporization
- Clausius-Claperyon Equation
- Boiling Point
- Critical Temperature and Pressure
- Surface Temperature and Pressure
Vaporization and Condensation
A molecule in a liquid which is moving towards the surface of the liquid may have enough kinetic energy to overcome the cohesive forces that hold the molecules in the liquid together and escape into the vapor (gas) phase. Likewise a molecule in the gas (vapor) phase that collides with molecules on the surface of the liquid can transfer energy to the liquid molecules and enter the liquid phase. This results in two phase transitions.
- Vaporization - the physical change of state where a chemical entity transforms from a liquid to a vapor.
- Condensation - the physical change of state where a chemical entity transforms from a gas (vapor) to a liquid.
This concept can also be extended to solids which undergo sublimation and deposition, and we can define two types of substances:
- Volatile Substance - a substance that can vaporize or sublime.
- Nonvolatile Substance - a substance that does not vaporize or sublime.
A volatile substance has a measurable vapor pressure, which is the partial pressure due to the molecules that have entered the gas phase. A nonvolatile substance does not have a measurable vapor pressure. It should also be noted that the terms "vapor" and "gas" are often used synonymously, although there is an implicit difference. A vapor phase molecule is a gas phase molecule, but it is implied that there can be particles in a solid or liquid phase too. That is, the system is, or was, heterogeneous. So if a sample of water entirely vaporizes (so there is no liquid left), it is a pure gas, but it is often referred to as a vapor, even though it was a pure gas.
In this chapter we will look at liquids and in the next chapter we will look at solids.
Vapor Pressure
The vapor pressure of liquid substance is the partial pressure due to the particles of that substance which have enough kinetic energy to overcome the cohesive forces near the surface of the liquid and enter the gas phase and form a vapor. The moment a chemical entity enters the gas phase it can hit the surface and condense back into the liquid phase (Figure \(\PageIndex{1}\)). If we ignore intermolecular interactions for the molecules that enter the vapor phase we can use the ideal gas law (PV=nRT) to correlate the vapor pressure to the number of particles in that phase, where the vapor pressure becomes the partial pressure due to the gas.
\[P_{A}=\frac{n_{A}RT}{V}\]
Vapor Pressure as an Equilibrium Pressure
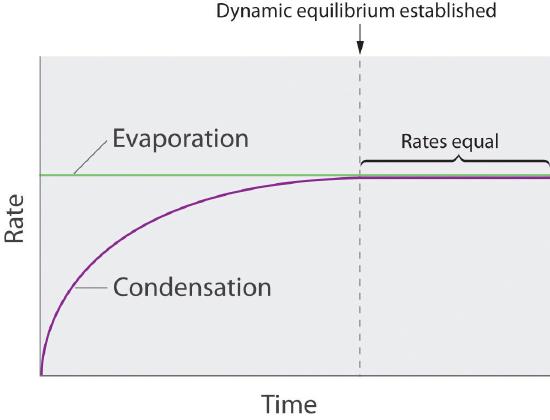
Although Equation 11.6.1 describes the pressure due to a liquid (A) whose molecules have entered the vapor phase, this is not always what chemists refer to as the vapor pressure. Chemists consider the Vapor Pressure to be the Equilibrium Pressure when the Rate at which Chemical Entities Vaporize Equals the Rate at which they Condense. If these rates are not equal the total number of molecules in the vapor phase changes, and so the vapor pressure changes. When they are equal you have a dynamic equilibrium, where individual particles are continually vaporizing and condensing, but the number of particles in the gas phase is constant and this results in a constant valued equilibrium pressure, which is what is referred to as the Vapor Pressure of that substance (above its liquid surface). These values do depend on the temperature (see below) and are often tabulated in thermodynamic tables as a function of the temperature.
Figure \(\PageIndex{2}\) illustrate this concept. Imagine you had a volatile liquid (a liquid which can vaporize) that completely filled a container so there was no space above the liquid, (so there could be no vapor). If you then instantly removed some of the liquid (say with a syringe), there would be a void above the liquid, but no molecules. They would start to evaporate, and the rate at which they evaporate would be related to the surface (the greater the surface area the faster the rate) and the temperature (which describes the average kinetic energy of the system. If the temperature and surface area are constant, then the rate of evaporation is constant (green line, Figure \(\PageIndex{2}\)). Initially there were no liquid particles in the gas phase, and so both the partial pressure (Figure \(\PageIndex{3}\)) and the initial rate of condensation (Figure \(\PageIndex{2}\)) are zero. As soon as some molecules enter the gas phase the partial pressure starts to rise (eq. 11.6.1 & Figure \(\PageIndex{3}\)), and some of these molecules can now collide with the surface and condense. As the number of particles in the gas phase increases the rate at which they collide with the surface increases and so the rate of condensation increases (Figure \(\PageIndex{2}\)). The number of particles in the gas phase keeps rising until the rate at which they evaporate (a constant value) equals the rate at which they condense, and a dynamic equilibrium pressure is achieved (the flat region of the curves in figures 11.6.2 & 3).
You need to be alert, that the constant valued equilibrium pressure is what chemists refer to as the vapor pressure, although if a system was not at equilibrium (left of the dotted line indicating the rates of condensation and vaporization are equal), we would still call that a vapor pressure. Figure \(\PageIndex{4}\) shows an apparatus for measuring the vapor pressure of a liquid. This is often a challenge for students, as the meaning of a word is often dependent on the context, (like is oxygen a monatomic atom "O" or a diatomic molecule "O2"?) Unless we are specifically describing a system that is not in equilibrium, the vapor pressure is the equilibrium pressure when the rates of evaporation equal condensation, and that has a specific value (which is a function of the temperature).
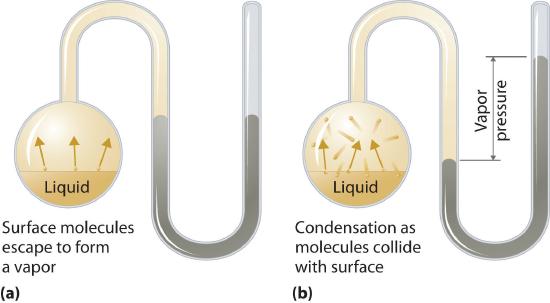
It needs to be emphasized that the vapor pressure is an equilibrium phenomena, and thus requires the gas to be in a closed container. If a container of water is closed, some will evaporate until it reaches its equilibrium vapor pressure. If the container is open to the atmosphere, all the water will eventually evaporate and you will have a gas, not a gas in equilibrium with its liquid.
Temperature Dependence of Vapor Pressure
We need to realize that concepts like liquid, gas, vaporization and condensation are not properties of individual chemical entities like a molecule or atom, but of a huge number of them, and need to be viewed as properties of an ensemble of particles, and not of individual atoms or molecules. A group of molecules has its energies distributed over a range of values resulting in velocity profiles like those in figure 11.6.5. The area under the curves are equal and represent the total number of molecules in a sample. As the temperature increases the curve flattens out and stretches to the right as more molecules move faster. If Vescape is the minimum velocity required to escape the surface of the liquid, only those molecules with a velocity equal or greater to this can escape (shaded part of the curve). It is clear from figure 11.6.5 that the fraction of molecules that can enter the gas phase (ratio of the shaded area to the total area under the curve) increases as the temperature rises, and so the number of molecules in the vapor phase increases as the temperature increases. This results in an increase in the vapor pressure as a function of temperature, which is plotted in figure 11.6.6 for a variety of substances.
It should be noted that just because a particle is moving fast enough to escape the surface does not mean it will, as it must also be moving in the correct direction.
In the next figure (11.6.6) we are looking at the vapor pressure as a function of temperature. This is an important diagram to understand as it relates molecular structure to the vapor pressure of a substance. That is, for molecules of similar mass, the stronger the intermolecular forces the lower the vapor pressure. We can sort of visualize an interplay between two different and opposing energies; increasing kinetic energy which favors the vapor phase, while increasing intermolecular forces favors the liquid phase. In the next section we will look into this in more detail, and you should reference back to this diagram.
Vapor Pressure: Intermolecular Forces, Particle Masses and the Enthalpy of Vaporization
From the Kinetic Molecular Theory of Gases and our studies of Grahm's Law of Effusion we know that the kinetic energy is proportional to the absolute temperature, and as we raise the temperature we raise the kinetic energy, 1/2mv2 (where m=mass and v=velocity), and thus a light molecule would move faster than a heavy one. Of course for a gas or a liquid you have an ensemble of particles and there is a velocity distribution function as in figure 11.6.7, with lighter particles tending to move faster than heavier ones (if they have similar intermolecular forces).
In Summary:
- Lighter molecules tend to move faster than heavier ones at a given temperature, and so increasing mass leads to a lowering of the vapor pressure.
- Stronger intermolecular forces suppresses the vapor pressure
These effects are evident in 11.6.6, where we can observe several trends at a given pressure and you should be able to explain these
- At a given temperature Pdiethyl ether>Pethanol>Pwater>Pethylene glycol. Diethyl ether is nonpolar and so even though it is the heaviest, has the weakest intermolecular forces and is easiest to vaporize. The other three compounds are not only polar, but have hydrogen bonds. Ethanol has one OH group while both water and ethylene glycol both have two, so even though it is heavier than water, is has a lower vapor pressure. Water and ethylene glycol both have two OH groups, but water is lighter, and so has a higher vapor pressure.
- At a given temperature Pwater>Pn-octane as even though the water has hydrogen bonds, the n-octane a 114 amu, weighting 6.3 times as much as the water, and being a large highly polarizable molecule with a lot of surface areas has strong London dispersion forces.
- Mercury has a very low vapor pressure and it needs to be realized that being a metal has metallic bonds, which we will cover in the next chapter. Although mercury is a liquid at standard conditions with a small vapor pressure, its vapor represents a serious health problem as it bioaccumulates.
The enthalpy of vaporization is the enthalpy required transform one mole of a substance from a liquid to a vapor, and is influenced by both the particles mass and its intermolecular forces. The higher the enthalpy of vaporization the more energy required to vaporize a substance and the lower the vapor pressure. Higher mass and stronger intermolecular forces result in a higher enthalpy of vaporization, and a lower vapor pressure.
Clausius-Clapeyron Equation: Mathematical derivation of the vapor pressure
In essence the vapor pressure above a liquid represents the partitioning of the particles between two phases, the liquid and the gas, that is, there is a fraction of the particles in each phase. There is an interplay between the enthalpy of vaporization (the higher it is, the more they want to be in the liquid phase) and the kinetic energy. The equation that describes this is the Clausius-Clapeyron, which is an exponential function. Like any exponential function, there are two forms, the exponential form, and the natural log form
\[\underbrace{P_{A}=ke^{-\frac{\Delta H_{vap,A}}{RT}}}_{\text{exponential form}} \label{11.6.2}\]
\[\underbrace{\ln P_{A}=-\frac{\Delta H_{vap,A}}{RT}+C}_{\text{logarithmic form}} \label{11.6.3}\]
where:
- PA=Vapor Pressure above volatile liquid "A"
- \(\Delta H_{vap,A}\) = Enthalpy of Vaporization for "A", always positive because it is endothermic
- R = 8.314J/mol-K (Ideal gas constant)
- T = Absolute Temperature in Kelvin (always positive
- k=a positive constant in units of Pressure, we will treat it as an "unknown constant", but it is related to the highest possible pressure, and will not be used in our calculations.
- C=lnk another constant we will not use
Lets take a closer look at the term
\[e^{-\frac{\Delta H_{vap,A}}{RT}}=\frac{1}{e^{\frac{\Delta H_{vap,A}}{RT}}}\label{11.6.4 }\]
- The term in eq. 11.6.4 itself is a fraction because the enthalpy of vaporization is endothermic (positive), and R and T are positive, so it is of the form \(\large\frac{1}{e^{positive\: number}}=\frac{1}{number>1}\)=a fraction
- \(\Delta H_{vap,A}\)
- As \(\Delta H_{vap,A}\) gets small and approaches zero, the fraction approaches 1 as e0=1
- As \(\Delta H_{vap,A}\) gets large and elarge number gets very large, and the reciprocal of a large number approaches zero.
- RT This is the molar kinetic energy term associated with three dimensional translational motion (Through the ideal gas law it is related to PV work, from section 5.1). Remember one of the postulates of the Kinetic Molecular Theory was that the Kinetic Energy of a gas is proportional to the absolute temperature, R is the molar proportionality constant (PV/n=RT).
- As T gets small, the fraction approaches zero
- 1/T gets large, so \(e^{\frac1{RT}}\) gets large and \(\frac{1}{e^{\frac1{RT}}}\) approaches zero
- As T gets large, the fraction approaches one
- 1/T gets small and approaches zero, so \(e^{\frac1{RT}}\) approaches e0, which is 1, and \(\frac{1}{e^{\frac1{RT}}}\) approaches one
- As T gets small, the fraction approaches zero
- \(\Delta H_{vap,A}\)
In Summary:
Small \(\Delta H_{vap,A}\) and high T favor large Vapor Pressures because the fraction \(e^{-\frac{\Delta H_{vap,A}}{RT}}\) approaches 1.
Large \(\Delta H_{vap,A}\) and low T favor low Vapor Pressures because the fraction \(e^{-\frac{\Delta H_{vap,A}}{RT}}\) approaches 0.
Remember, at constant pressure, the smallest T is defined by the freezing point, and the highest T is defined by the boiling point, and only in this range do you a system where a vapor can be in equilibrium with it liquid. Below this temperature the liquid freezes, and above it have a gas (once they system has reached equilibrium).
From eq. 11.6.3, the slope of the linear plot of the lnPv as a function of the reciprocal temperature (1/T) is equal to -\(\Delta H_{vap,A}\)/R and can be used to measure the enthalpy of vaporization.
Two State Form of the Clausius-Claperyron Equation:
The two state approach will be used over and over this semester, and was introduced in gen chem 1 in the gas laws (section 10.2.4) when it was applied to the ideal gas equation, and here is is applied to the Clausius-Claperyon Equation, which is an exponential equation. Note, there are two forms, the exponential and the logarithmic.
Exponential form:
Knowing Pvap at one T and\(\Delta H_{vap,A}\) you can calculate it at another temperature. You start by dividing eq 11.6.2 at one state (state 1: Pvap,1,T1) by the same equation at another state (state 2 :Pvap,2,T2.)
\[\frac{P_{v,1}}{P_{v,2}}=\frac{ke^{-\frac{\Delta H_{v}}{RT_1}}}{ke^{-\frac{\Delta H_{v}}{RT_2}}}=\frac{e^{-\frac{\Delta H_{v}}{RT_1}}}{e^{-\frac{\Delta H_{v}}{RT_2}}}={e^{-\frac{\Delta H_{v}}{R}(\frac{1}{T_1}-\frac{1}{T_2})}}\label{11.6.5 }\]
If you know the vapor pressure at one Temperature, (T2), you can rearrange the above equation to determine it at another temperature (T1)
\[P_{v,1}=P_{v,2}\: {e^{\frac{\Delta H_{v}}{R}(\frac{T_1-T_2}{T_2T_1})}}\label{11.6.6}\]
Logarithmic Form:
You can take the natural log of eq. 11.6.5 and solve for the enthalpy of vaporization
\[ln(\frac{P_1}{P_2})=-\frac{\Delta H_V}{R}\left ( \frac{1}{T_1}-\frac{1}{T_2} \right )\label{11.6.7}\]
This can be rearranged to
\[\Delta H_V=\frac{R}{\frac{1}{T_2}-\frac{1}{T_1}}ln(\frac{P_1}{P_2})\label{11.6.8}\]
or
\[\Delta H_V=\frac{RT_1T_2}{T_1-T_2}ln\frac{P_1}{P_2}\label{11.6.9}\]
There are advantages to the forms represented in equations 11.6.6 and 11.6.9 in that they are easier to "read". You know that as T goes up, the vapor pressure goes up, and you know that the enthalpy of vaporization must be positive.
Lets look at 11.6.6:
- If T1<T2, then the exponent on the right side is negative, and a fraction, meaning P2>P1, which makes sense.
- If T1>T2, then the exponent on the right side is positive, the number is greater than 1, meaning P2<P1, which makes sense.
Lets look at 11.6.9
- If T1<T2, then P1<P2 ,
- The 1/(T1-T2) term is negative
- P1/P2 ,is a fraction and ln of a fraction is a negative number
This means the enthalpy of vaporization is a positive number as dividing a negative number into a positive number gives a negative number, and it makes sense.
- If T1>T2, then P1>P2 ,
- The 1/(T1-T2) term is positive
- P1/P2 ,is greater than 1 and the ln is a positive number
Once again, the enthalpy of vaporization is positive.
The Clausius-Claperyon equation is the first equation we cover this semester that is of this form. As the semester progresses we will have other similar equations, like the Arrhenius equation (exam 2) and Gibbs Free Energy Equation (exam 4). These may be a bit intimidating now, but by the end of the semester you will be able to manipulate these equations.
Exercise \(\PageIndex{1}\)
Calculate the vapor pressure of water at 45o C if it is 12.79 torr at 15o C, given:
| Substance | \(\Delta H_{f}^{o}\) |
|---|---|
| H2O(l) | -285.8 |
| H2O(g) | -241.8 |
- Answer
-
72.27 Torr, which is not far off from the published value of 71.93 Torr. Note, we first solved the equation and then assigned the states. There are many correct forms this equation can take. At the end of the problem you should always ask, does my answer make sense? In this case we raised the temperature, which caused the vapor pressure to go up, and that makes sense. If in a problem you raise the temperature, and the pressure goes down, you need to take a closer look at your work to see if you can find your mistake. Usually it is either a math mistake, or not properly assigning your data to the algebraic variables. That is why I create a table with a column for each state, as it reduces the chance of switching the values.
Boiling Point
The definition of the boiling point is when the vapor pressure equals ambient (surrounding) pressure. At this pressure molecules within the bulk of the liquid turn to a vapor and bubble up through the liquid. This is the difference between boiling and evaporation.
What is the difference between boiling and evaporation?
- Evaporation - surface phenomena where liquid molecules at the surface vaporize and escape the cohesive (attractive) forces and enter the gas phase
- Boiling - a bulk fluid phenomena where the liquid state becomes unstable and spontaneously forms a vapor, even if it is not near the surface. This occurs when the vapor pressure equals ambient pressure. When you see water boil, those bubbles are not air bubbles, but water vapor.
What are the two ways to boil a substance
- At constant pressure (isobar), raise the Temperature until the vapor pressure equals the ambient pressure
- At constant temperature (isotherm) lower the ambient pressure until it equals the vapor pressure.
This explains how a pressure cooker or autoclave works to cook food or sterilize equipment because you can raise the temperature above 100oC. It also explains why you have to boil an egg longer in the mountains, because the ambient pressure is lower. Table 11.6.1 shows how the boiling pt. a different locations on the earth changes as the elevation changes (remember, the pressure is due to the "column of air" on top of you, and the higher up you are, the less air their is above you.
What is meant by NORMAL BOILING POINT?
The normal boiling point is the temperature a substance boils at 1 atmosphere pressure
| Place | Altitude above Sea Level (ft) | Atmospheric Pressure (mmHg) | Boiling Point of Water (°C) |
|---|---|---|---|
| Mt. Everest, Nepal/Tibet | 29,028 | 240 | 70 |
| Bogota, Colombia | 11,490 | 495 | 88 |
| Denver, Colorado | 5280 | 633 | 95 |
| Washington, DC | 25 | 759 | 100 |
| Dead Sea, Israel/Jordan | −1312 | 799 | 101.4 |
Exercise \(\PageIndex{1}\)
Given the following melting and boiling points, give two reasons why Iodine is a solid and fluorine is a gas at STP?
| Halogen | mp(K) | bp(K) |
|---|---|---|
| F2 | 53.5 | 85.0 |
| Cl2 | 172.2 | 238.6 |
| Br2 | 265.9 | 331.9 |
| I2 | 386.7 | 457.5 |
- Answer
-
All of the above molecules are nonpolar and have London Dispersion forces interacting between them (Instantaneous dipole-induced dipole).
- Reason 1: The fluorine molecules are lighter and thus tend to move faster at a given temperature than the heavier iodine molecules (look at velocity profiles).
- Reason 2: Iodine is more polarizable and thus has stronger intermolecular forces. It is more polarizable because it has (a) more electrons and (b) a larger volume, that results in its electrons being less tightly held (and thus more polarizable).
Boiling points are an indicator of intermolecular forces, and we will look at the phenomena of boiling in more detail in a later section of this chapter. From the kinetic molecular theory of gases we learned that the kinetic energy of a molecule is proportional to its absolute temperature, where KETranslation = 1/2mv2, (m is the mass, and v is the velocity). We also learned that there is a velocity profile with different molecules moving at different speeds, but that heavier molecules tend to move slower than lighter ones (remember macroscopic observables like liquids and boiling are the result of the interactions of a huge number of molecules which possess a distribution of energies). So all things equal, we would anticipate that it is easier to boil a lighter molecule than a heavier one, and we would predict the heavier one to have a higher boiling point.
Class Activity
Boiling Point and Hydrogen Bonds
Figure \(\PageIndex{4}\). shows the trend for various hydrides of different families of the periodic table. Our predictions based on molar mass work for group IV (CH4 through SnH4), but does not work for groups VII, VI and V, where the hydrides of the second period (N,O,F) have higher boiling points than would be predicted from their mass trends.
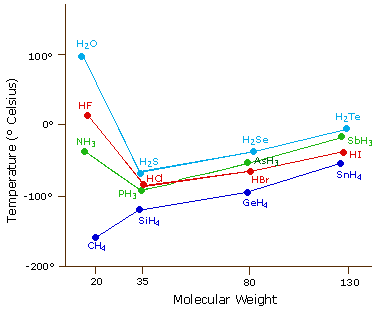
Figure \(\PageIndex{10}\): Periodic trends in boiling point for various hydrides.
There are a multitude of questions that can come out of figure \(\PageIndex{4}\), and you should familiarize yourself with this figure. You should also revisit this figure after we have covered the section on boiling. Right now let it suffice that to boil a substance you need to overcome the intermolecular forces that hold the liquid together (the cohesive forces), and that as you increase the temperature you increase the kinetic energy of the molecules (so they can escape the liquid and become a vapor).
First, lets look at the group 4 hydrides (CH4, SiH4, GeH4& SnH4),. As we go down the table from carbon to silicon to germanium to Tin we see an increase in the boiling points. These are symmetric nonpolar molecules and there are two reasons why going down this family shows an increase in the boiling point.
- Going down group 4 the mass increases, requiring a higher temperature for molecules to gain enough kinetic energy to vaporize.
- Going down the table the valence electrons occupy more diffuse orbitals, resulting in a higher polarizability, which in turn results in larger London dispersion forces.
So both of these trends would indicate an increase in the boiling point as we go down the family.
Second, ammonia, hydrofluoric acid and water show a deviation in this trend. That is, they are lighter, but there is an increase in their boiling points. This is due to hydrogen bonding. That is, although these molecules are lighter, they have very strong intermolecular forces, which must be overcome for them to boil.
Third, water has a higher boiling point than HF, yet fluorine is more electronegative than oxygen, it is also smaller, and so you would expect the HF hydrogen bond to be stronger than the OH hydrogen bond. In fact, this is all true, and what this argument does not take into account is the number of hydrogen bonds. That is, the cohesive forces that hold the liquid together are not just the strength of the bonds, but also the number of bonds. Each HF molecule has one H, and 3 lone pairs on the fluorine. So in a macroscopic system like a mole of HF (remember that to be a liquid, you need a lot of molecules), each HF would on average be involved with 2 bonds, one involving the hydrogen (hydrogen donor), and one involving a fluorine lone pair (hydrogen acceptor), and simple speaking, there are not enough hydrogens to use up all the lone pairs, (two of the fluorine's lone pairs are not involved in H bonds.) In the case of water, the number of lone pairs equals the number of hydrogens, and so each water molecule can on the average, be involved with 4 hydrogen bonds. So even though the individual hydrogen bonds in water may be weaker than in HF, there are more of them, making the boiling point of water higher than HF.
Exercise 11.5.2: Look at Real Molecules (Exam Material)
Before reading on, look at the following three molecules and their boiling points, and try and answer the following 2 questions.
1. Why is pentane's boiling point so much lower than the other two?
- Answer
-
Pentane is non polar and the other two have hydrogen bonds through the OH group.
2. Why does butan-1-ol have a higher boiling point than 2-methylpropan-1-ol?
- Answer
-
Both of these molecules are isomers with the same chemical constituents (C4H10O) and both have an OH group than can be involved with hydrogen bonds. But butan-1-ol is more diffuse, thus more polarizable and has stronger van der Waals (London dispersion) interactions
Exercise \(\PageIndex{2}\)
Predict the trend in boiling points for the following linear hydrocarbons: CH4, C2H6, C3H8, C4H10 and C5H12:
- Answer
-
CH4 < C2H6 < C3H8 < C4H10 < C5H12. because that is the direction of (a) increasing mass and (b) increasing polarizability and thus increasing Lodon Dispersion forces.
Exercise \(\PageIndex{3}\)
Rank the following in order of increasing boiling point.
1. HF, HCl, HBr and HI
- Answer
-
HCl < HBr < HI < HF. HI is greater than HBr because of its mass, which in turn is greater than HCl, but the lighter HF breaks this trend because it has strong hydrogen bonds, and thus even though it is the lightest, if has the strongest intermolecular forces and thus has the highest boiling point. Note here the trends of mass and of polarity go in opposite directions, in that HCl is more polar the HBr, which is turn is more polar than HI.
Surface Tension, Capillary Action and Viscosity
Introduction
Cohesive forces are the forces of attraction between particles within a substance (or phase), and adhesive are between two different substances (or phases). These can explain properties like surface tension and viscosity, and phenomena like capillary action and why meniscus sometimes are concave and other times are convex.
- Cohesive Forces - the intermolecular forces of attraction holding the particles of a liquid together.
- Adhesive Forces - the intermolecular forces between a liquid's molecules and another substance, like a glass surface.
You should be able to predict trends based on intermolecular forces for these.
Surface Tension
On the surface of a liquid, there are negligible adhesive forces attracting the liquid to the gas phase, but substantial cohesive forces attracting the liquid to itself. The result is that particles near the surface of the liquid feel a net force pulling them into the liquid, with a resulting contraction in volume, which is why liquids form drops. The surface tension is related to the force required to increase the surface area, and can explain why objects like a paper clip can float if they are on the surface, but sink if they are placed below the surface. The stronger the intermolecular forces, the greater the surface tension.
 Figure \(\PageIndex{10}\): Image showing how surface area contracts due to cohesive forces (public domain Wikipedia)
Figure \(\PageIndex{10}\): Image showing how surface area contracts due to cohesive forces (public domain Wikipedia)
1:24 youtubeYoutube on Surface Tension by Berkeley Lab's Molecular Foundry, https://youtu.be/ciqNNRlS2yA .
Capillary Action
Through capillary action polar liquids like water can rise up narrow diameter tubes against the force of gravity.
In reality, not all substances rise up, some even fall down. This is the result of the interaction of a liquid with a solid, and there are two types of forces at play, cohesive and adhesive.
Glass is based on silicon dioxide (like sand) and the surface has a lot of hydroxy groups (OH) that can participate in hydrogen bonds. This results in strong adhesive forces with polar solvents like water, and if the adhesive forces are greater than the cohesive forces, the water will crawl up the small capillary tube as illustrated in figure 11.6.m.
Meniscus: The meniscus curves up when the adhesive forces > cohesive and down when the cohesive forces > adhesive. In the case of water and glass, a slight film of water creeps up the surface of large diameter devices like burettes and graduated cylinders, and you read from the bottom of the meniscus. In the case of instruments like mercury thermometers and barometers, you read from the top of the meniscus.
- Adhesive > Cohesive - meniscus goes up
- Cohesive > Adhesive - meniscus goes down
Figure \(\PageIndex{13}\): Diagram showing different types of meniscus.
Viscosity - Resistance to Flow
The viscosity of a fluid is a measurement of its resistance to flow. A high viscous fluid is like molasses and has a large resistance to flow, while a low viscous fluid would be like water and have a low resistance to flow. The following 2 You Tubes demonstrate high and low viscous fluids.
0.33 min Youtube showing a high and low viscous fluids being poured, https://youtu.be/vNzTYzjLgKE .
0.33 min YouTube animation showing lead ball being dropped into two cylinders, one with a high viscous fluid and one with a low viscous fluid.
The units of viscosity are the poise (P) or centipoise (cP
1P = 0.1N s m-2 = 0.1 Pascal-second
1cP = 0.001N s m-2
| Common liquid |
Viscosity /cP |
Surface tension /N m-1 |
|---|---|---|
| Diethyl ether | 0.233 | 0.0728 |
| Chloroform | 0.58 | 0.0271 |
| Benzene | 0.652 | 0.0289 |
| Carbon tetrachloride | 0.969 | 0.0270 |
| Water | 1.002 | 0.0728 |
| Ethanol | 1.200 | 0.0228 |
| Mercury | 1.554 | 0.436 |
| Olive oil | 84 | - |
| Castor oil | 986 | - |
| Glycerol | 1490 | 0.0634 |
| Glasses | very large | - |
Viscosity is a strong function of temperature as indicated in table 11.6.3
| Temperature /°C |
Viscosity /cP |
|---|---|
| 20 | 1.002 |
| 40 | 0.653 |
| 60 | 0.467 |
| 80 | 0.355 |
| 100 | 0.282 |
Automobile oil lubricates you car's engine and are rated by their viscosity with an SAE (Society of Automotive Engineers) number with SAE 5 being low viscosity oil (appropriate for winter conditions) and SAE 40 or 50 being more viscous and appropriate for summer conditions.
Supercritical Fluids
At very high pressure and temperatures the boundary between the a gas and its liquid disappears. That is, at high temperature there is a lot of kinetic energy, which dominates the intermolecular forces and the system behaves like a gas with very low viscosity (like a gas), but at high pressure the particles are pushed close to each other and the density rises to that of a liquid.
d
At the Critical point the two fluid phases become one, and there is not boundary between them. At pressures and temperatures above the critical point you have a supercritical fluid.
There are two fluid phases, the gas and the liquid.
- Gas Phase,
- favored at low pressure (particles are far apart)
- Favored at high temperature (particles have high kinetic energy make attractive forces negligible)
- Liquid Phase
- Favored at high pressure (molecules are close to each other)
- Favored at low temperature (attractive forces are able to compete with motion and keep molecules together
The following video was created at ETH Zurich as part of a Carbon Capture and Storage Exhibit. In this video they have two substances of different densities that "float" on liquid carbon dioxide at 28oC and 69 bar, but one is more dense than supercritical carbon dioxide. They then raise it to the critical point 31.1oC and 73.9 bar and the phases merge, with the one float sinking, and the other moving around. They then return to the initial condition, and the boundary reforms with both floats returning to the surface.
YouTube developed by ETH Zurich describing supercritical fluids https://youtu.be/P9EftqFYaHg
We will return to supercritical fluids and the critical point in the next chapter when we cover phase diagrams.
Supercritical fluids can occur in underwater volcanoes deep below the surface where the pressure is high and the
 Figure \(\PageIndex{1}\): Black smokers, it is likely the volcanic fluids are at supercritical conditions although they cool when they reach the surface, but on occasions these can be supercritical. (Public Domain, P. Rona, NOAA Photolibrary)
Figure \(\PageIndex{1}\): Black smokers, it is likely the volcanic fluids are at supercritical conditions although they cool when they reach the surface, but on occasions these can be supercritical. (Public Domain, P. Rona, NOAA Photolibrary)
In Class Activities
ADAPT \(\PageIndex{1}\)
ADAPT \(\PageIndex{2}\)


