6.2: Quantization: Planck, Einstein, Energy, and Photons
- Page ID
- 52778
Learning Objectives
- Explain how the study of Blackbody Radiation lead to the understanding of quantized energy
- Relate wavelength and frequency to the energy associated with electromagnetic radiation
- Summarize the photoelectric effect and its impact on discovering the photon
Introduction
In the last section we saw that c=\(\lambda \nu\), which means the frequency and wavelength of light are inversely related, that is \(\nu =\frac{c}{\lambda }\), and so doubling the wavelength halves the frequency. In this section, we shall define the concept of a photon of light and see how planck's equation relates the frequency and wavelength to the energy of light.
Planck's Equation and Black Body Radiation
A black body is an object that absorbs light of all frequencies, and if heated, a black body will emit light of a characteristic spectrum. It could be experimentally observed that both the frequency (color) and the intensity (amount) of the light emitted by a black body is a function of its temperature, as indicated in Figure 6.2.1. By intensity, we mean how much light of a given color, so as the temperature goes from 3000K to 6000K we see that not only is more light given off, but that its color has shifted from the red to the blue.
 |
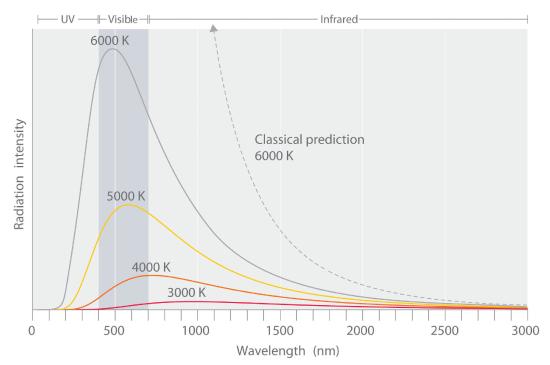 |
Figure \(\PageIndex{1}\): The intensity of light being emitted by a black body is a function of the temperature. As the temperature goes up two things happen. First, the intensity of light increases, and second, there is a blue-shift. That is, at low temperatures the light is red, and as it heats up, it moves towards the ultraviolet. Image on right from Wikipedia.
Phet Simulation \(\PageIndex{1}\): Interactive black body spectrum showing how the both the intensity and peak wavelength are a function of temperature.
It can be observed that as the energy goes up the intensity goes down, and around 1900 Max Planck accounted for this by considering the light to be emanating from oscillations that he associated with atoms of a specific frequency \(\nu\). He recognized that different particles could oscillate at different frequencies, and the energy of the oscillation was proportional to the frequency, as given by Planck's Law.
\[E = h\nu \label{6.2.1}\]
Today Planck's constant is considered to be a fundamental physical constant (section 1B.1.3) and is in fact used in the modern definition of the kilogram. The current defined value of the Planck's constant is:
\[h \equiv 6.626070040(81)×10^{-34} J \cdot s (joule \cdot seconds)\]
In this class we will typically use it to 4 significant digits.
\[ h = 6.626 × 10^{-34} J \cdot s\]
Planck actually related the intensity of light to an integer times this value, but to truly understand this equation we need to look at the photoelectric effect, where we will see that n is related to the number of particles oscillating at the frequency \(\nu\).
\[I = nh\nu\]
To understand blackbody radiation and Figure 6.2.1 we need to rewrite Planck's law in terms of wavelength
\[E=h\nu =h\frac{c}{\lambda } \] \[ I=nh\nu =nh\frac{c}{\lambda } \].
The blue shift in the wavelength is because as E goes up, \(\lambda\) goes down. The increase in intensity is because as the temperature rises, n goes up.
Example \(\PageIndex{1}\)
A ruby laser, a device that produces light in a narrow range of wavelengths emits red light at a wavelength of 694.3 nm (Figure \(\PageIndex{4}\)). What is the energy in joules of a single photon?
Given: wavelength
Asked for: energy of single photon.
Strategy:
- Use Equation \(\ref{6.2.1}\) and the relationship between wavelength and frequency to calculate the energy in joules.
Solution:
The energy of a single photon is given by \[E = h\nu = \dfrac{hc}{λ}.\]
Exercise \(\PageIndex{1}\)
An x-ray generator, such as those used in hospitals, emits radiation with a wavelength of 1.544 Å.
- What is the energy in joules of a single photon?
- How many times more energetic is a single x-ray photon of this wavelength than a photon emitted by a ruby laser?
- Answer a
-
\(1.287 \times 10^{-15}\; J/photon\)
- Answer b
-
4497 times
Exercise \(\PageIndex{2}\)
When we see light from a neon sign, we are observing radiation from excited neon atoms. If this radiation has a wavelength of 640 nm, what is the energy of the photon being emitted?.
- Answer
-
We use the part of Planck's equation that includes the wavelength, λ, and convert units of nanometers to meters so that the units of λ and c are the same.
\[E=\dfrac{hc}{λ} onumber\]
\[\begin{align*}
E&=\mathrm{\dfrac{(6.626×10^{−34}\:J\cancel{s})(2.998×10^{8}\:m\cancel{s}^{−1})}{(640\cancel{nm})\left(\dfrac{1\:m}{10^9\cancel{nm}}\right)}}\\
E&=\mathrm{3.10×10^{−19}\:J}
\end{align*}\]
Exercise \(\PageIndex{3}\)
The microwaves in an oven are of a specific frequency that will heat the water molecules contained in food. (This is why most plastics and glass do not become hot in a microwave oven-they do not contain water molecules.) This frequency is about 3 × 109 Hz. What is the energy of one photon in these microwaves?
- Answer
-
2 × 10−24 J
Photoelectric Effect
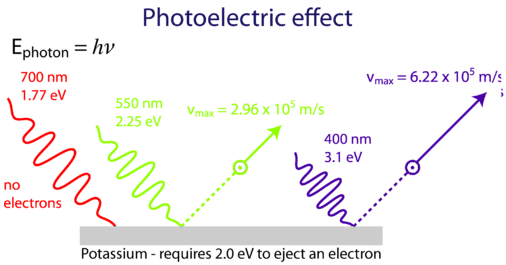
The photoelectric effect was the observation that an electric current can be generated if light of certain frequencies hits the surface of a metal object, but that light of only certain colors can do this. In fact, for each type of metal there was a maximum wavelength that could eject an electron, and any light with a longer wavelength would have no effect, even if you increased its intensity. Einstein recognized that this could be explained by Planck's equation where one could define a "particle of light" or photon as having a fundamental energy of h\(\nu\).
\[E_{photon} = h\nu\]
Einstein was able to use Planck's quantization hypothesis to explain the photoelectric effect. As indicated in Figure \(\PageIndex{2}\) a minimum energy of 2.0 eV is required to eject a photon off of potassium, and so red light would not work, while green and purple would.
The following video shows the photoelectric effect,
Video \(\PageIndex{1}\): 1'35" YouTube demonstrating the photoelectric effect. Credits go to College of Chemistry, University of California, Berkeley
Developed by Professor Alex Pines and Dr. Mark Kubinec with the support of The Camille & Henry Dreyfus Foundation (https://youtu.be/kcSYV8bJox8)
This second video by BestOfScience is a bit long, but summarizes this Chapter
Exercise \(\PageIndex{4}\)
Identify which of the following statements are false and, where necessary, change the italicized word or phrase to make them true, consistent with Einstein's explanation of the photoelectric effect.
- Increasing the brightness of incoming light increases the kinetic energy of the ejected electrons.
- Increasing the wavelength of incoming light increases the kinetic energy of the ejected electrons.
- Increasing the brightness of incoming light increases the number of ejected electrons.
- Increasing the frequency of incoming light can increase the number of ejected electrons.
- Answer a
-
False, brightness is related to the intensity of light and a bright light has a lot of photons, not the energy of each photon. If the light has enough energy to eject an electron this will increase the current (the number of electrons), but not the energy of each electron. If the photon does not have enough energy to eject an electron, increasing the brightness of that color of light will have no effect.
- Answer b
-
False, increasing the frequency, how fast the wave oscillated increases the energy. In fact the effect is the opposite, and a long wavelenght oscillates slower and so this would decrease the energy.
- Answer c
-
True, a bright light has a large flux (number of photons per unit surface area), and so with more photons striking the metal surface the number of electrons ejected increases.
- Answer d
-
True and False. If the initial frequency is below the threshold value, then initially no current flows and as the frequency is increased a current starts to flow once that threshold energy is reached. But after that value is reached, further increasing the frequency does not increase the flow of electrons (the current), but it does increase the energy of each ejected electron.
Exercise \(\PageIndex{5}\)
Calculate the threshold energy in kJ/mol of electrons in aluminum, given that the lowest frequency photon for which the photoelectric effect is observed is \(9.87 \times 10^{14}\; Hz\).
- Answer
-
\(3.94 \: kJ/mol\)
Contributors and Attributions
Robert E. Belford (University of Arkansas Little Rock; Department of Chemistry). The breadth, depth and veracity of this work is the responsibility of Robert E. Belford, rebelford@ualr.edu. You should contact him if you have any concerns. This material has both original contributions, and content built upon prior contributions of the LibreTexts Community and other resources, including but not limited to:
- Ronia Kattoum (UALR)
- Paul Flowers, et al. Open Stax (examples and exercises)
- anonymous


