Skip to main content
Chemistry LibreTexts

2.8: Atoms and the Mole

  1. Last updated
  2. Save as PDF
  • Page ID
    50436

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    learning objectives

    • Define the mole
    • Differentiate molar mass from molecular weight
    • Calculate molar mass of a compound from its formula

    The Mole

    The mole is a unit of measurement that defines quantity as a counted number. It is the value of Avogadro's constant, one of the seven SI base units (review section 1B1.3.1) and the modern definition is the number of entities defined by , 6.02214076 x 1023 . This may not be intuitive, but this is an exact definition and there is no uncertainty to it.

    1 dozen of eggs = 12 eggs

    1 mole of eggs = 6.02214129 x1023 eggs

    Note, the symbol for mole is mol and not M (which means mol/liter).

    To appreciate the magnitude of Avogadro’s number, consider a mole of pennies. Stacked vertically, a mole of pennies would be 4.5 × 1017 mi high, or almost six times the diameter of the Milky Way galaxy. If a mole of pennies were distributed equally among the entire population on Earth, each person would have more than one trillion dollars. The mole is so large that it is useful only for measuring very small objects, such as atoms.

    Students need to memorize this number to 4 significant digits (6.022 x 1023) but may need more if they use it in a calculation where using 4 significant digits determines the wrong number of significant digits in the answer. So if you multiply a six digit number like 1.00000 by Avogadro's number, you should use 7 digits for avagadro's number, ie., 6.022140 x 1023 .and the answer is 6.02214 x 1023 and not 6.022 x 1023.

    Video \(\PageIndex{1}\) Ted-Ed video on "How big is a mol?" by Daniel Dulek

    Molar Mass

    The molar mass is the mass of 6.022x1023) atoms or compounds (molecules or ionic formula).

    Substance (formula) Atomic, Molecular, or Formula Mass (u) Molar Mass (g/mol) Structure
    Helium (He) 4.0026 (atomic mass) 4.0026 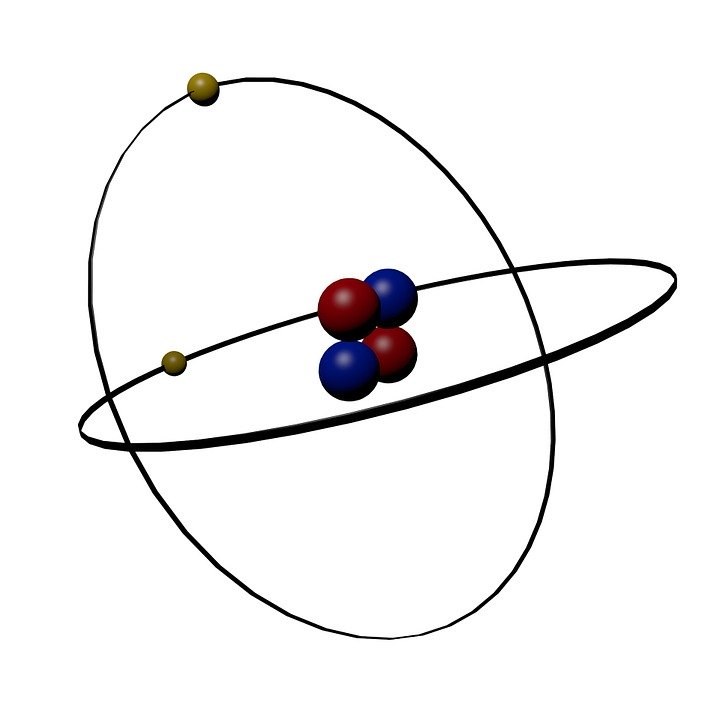Helium, Atom, Animation
    Pixabay
    ethanol (C2H5OH) 46.069 (molecular mass) 46.069 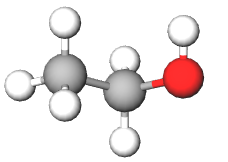clipboard_ef43b53f56d39d1359b88c5c768cf0f9c.png
    calcium phosphate [Ca3(PO4)2] 310.177 (formula mass) 310.177 File:Ca3(PO4)2 from crystallography.jpg
    wikimedia commons

    Figure \(\PageIndex{1}\): Comparison of atomic and molar mass for atom, molecule and ionic compound

    The molar mass is often called the molecular weight or the formula weight (fw). Technically speaking, molecular weight only works for molecules, where it is the weight of one mole of molecules, where each molecule is a particle. For ionic compounds you could have one piece of crystal that has a mole of its constituent elements as defined by the ionic formula, but there is only one particle, and so it is better to consider its formula mass, or formula weight. We will use the symbold fw to indicate formula weight

     

    Molar Mass of Elements

    The importance of a mole is that if you have one mole of an element, the mass of the mole in grams is the same as the average mass of each element in Daltons (u). So if the average isotopic mass of an atom in a sample of carbon weights 12.011 u, then one mole of a sample of carbon weights 12.011 grams.

    clipboard_efd1b4e60927522bbda619018b2c22aa2.png clipboard_e22204d715a68aad76ff23f06a230cc22.png
    clipboard_e13235a5a43bb64f27f61bd24639d26fb.png clipboard_edf350337d90bdbc053f035a890cc1810.png

    Figure \(\PageIndex{2}\): The two samples of carbon (left) and copper (right) have the same number of molecules (1 mol or 6.022x1023) but different masses and volumes. Note, these are tared weights, that is, the weight of the container was subtracted from the displayed value (see use of analytical balances).

    Exercise \(\PageIndex{1}\)

    Which has a greater number of particles? Which of the following has a greater mass?

    A) 2.5 moles of He

    B) 2.5 moles of Ar

    Answer

    Both have the same number of particles because there are 2.5 moles of each. That is similar to saying 2.5 dozen of donuts is the same number of items as the 2.5 dozen of cars. However, 2.5 moles of cars is going to have a larger mass than 2.5 dozen of trucks. By the same token, 2.5 moles of Ar is going to have more mass than 2.5 moles of He, even if they have the same number of particles.

    Molar Mass of Compounds

    Molecular

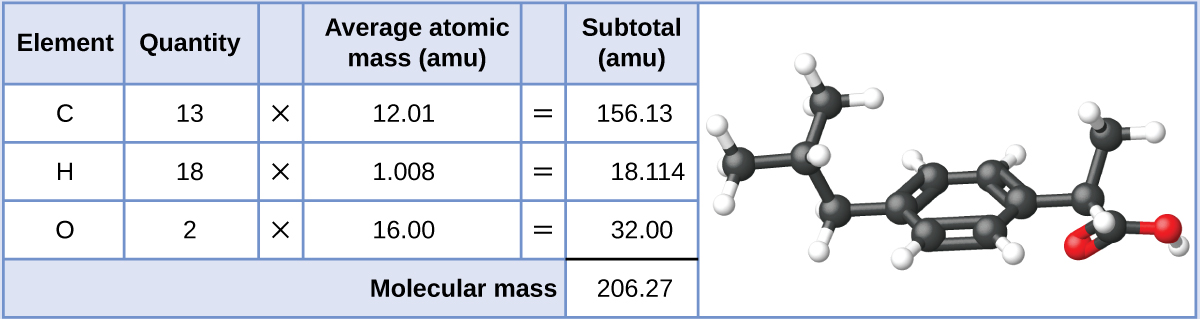
    Ibuprofen, C13H18O2, is a covalent compound and the active ingredient in several popular nonprescription pain medications, such as Advil and Motrin.

    CNX_Chem_03_01_ibuprofenmass_img.jpg
    Figure \(\PageIndex{3}\): Calculation of molar mass of molecule (ibuprofen) (adopted from OpenSTAX)

    Ionic

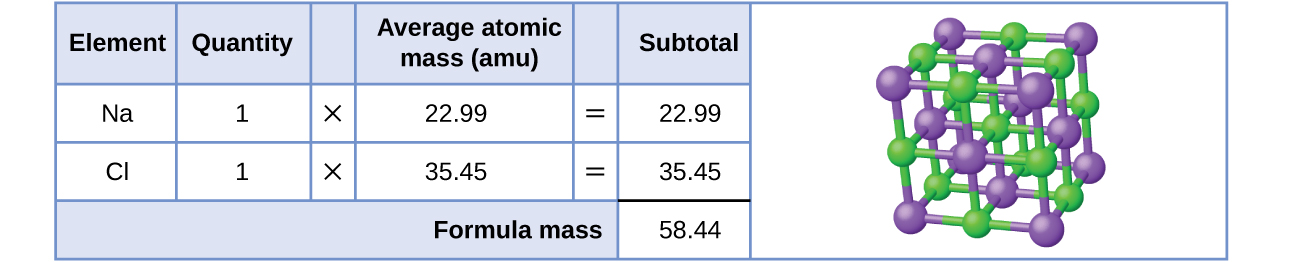
    Remember Ionic compounds are discrete cations and anions combined to form a neutral crystal lattice. The formula for an ionic compound is the lowest whole number ratio of cations to anions and is not defined by the bonds, and there is no discrete "molecule" like there was for ibuprofen. Sodium chloride for example has the formula of NaCl, even though each sodium is bonded to 6 chlorines, while each chlorine in turn if bonded to 6 sodiums forming a lattice in 3 diensional space. Sodium chloride is an ionic compound composed of sodium cations, Na+, and chloride anions, Cl−, combined in a 1:1 ratio. The formula mass for this compound is computed as 58.44 amu (Figure \(\PageIndex{4}\) ), even though a real sample has many more sodium and chloride ions within its crystal structure.

    A table and diagram are shown. The table is made up of six columns and four rows. The header row reads: “Element,” “Quantity,” a blank space, “Average atomic mass (a m u),” a blank space and “Subtotal (a m u).” The first column contains the symbols “N a”, “C l,” and a merged cell. The merged cell runs the length of the first five columns. The second column contains the numbers “1” and “1” as well as the merged cell. The third column contains the multiplication symbol in each cell except for the last, merged cell. The fourth column contains the numbers “22.99” and “35.45” as well as the merged cell. The fifth column contains the symbol “=” in each cell except for the last, merged cell. The sixth column contains the values “22.99,” “35.45,” and “58.44.” There is a thick black line below the number “35.45.” The merged cell under the first five columns reads “Formula mass.” To the left of the table is a diagram of a chemical structure. The diagram shows green and purple spheres placed in an alternating pattern, making up the corners of eight stacked cubes to form one larger cube. The green spheres are slightly smaller than the purple spheres.
    Figure \(\PageIndex{4}\): Calculation of molar mass of ionic compound (table salt, NaCl) (adopted from OpenSTAX)

    You can also calculate the molar mass of polyatomic ions. This is often called molecular weight or formula weight.

    Example: The molar mass of sulfate (SO4-2)

    1 mole S (1)(32.07) = 32.06g
    4 mole O (4)(16.00) = 64.00g
    1 mole SO4-2 = 96.06g

    Practice

    Exercise \(\PageIndex{2}\)

    What is the molar mass for each of the following molecules?

    1. Aluminum Sulfate
    2. Benzene (C6H6)
    3. Acetylene (C2H2)
    4. Water
    5. Hydrogen Peroxide
    Answer a

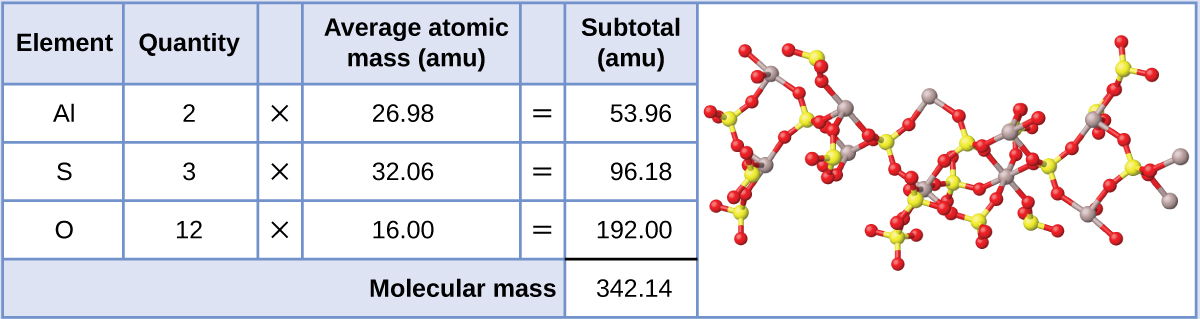
    <div data-mt-source="1"><img alt="A table is shown that is made up of six columns and five rows. The header row reads: “Element,” “Quantity,” a blank space, “Average atomic mass (a m u),” a blank space, and “Subtotal (a m u).” The first column contains the symbols “A l,” “S,” “O,” and a merged cell. The merged cell runs the length of the first five columns. The second column contains the numbers “2,” “3,” and “12” as well as the merged cell. The third column contains the multiplication symbol in each cell except for the last, merged cell. The fourth column contains the numbers “26.98,” “32.06,” and “16.00” as well as the merged cell. The fifth column contains the symbol “=” in each cell except for the last, merged cell. The sixth column contains the values “53.96,” “96.18,” “192.00,” and “342.14.” There is a thick black line under the number 192.00. The merged cell under the first five columns reads “Molecular mass.” To the right of this table is a ball-and-stick structure. It shows yellow and grey sphere connected to red spheres in a complex pattern. The yellow and grey spheres are similar in size, but the red spheres appear to be smaller by comparison." data-cke-saved-src="http://cnx.org/resources/69320dd9501e62acfadfea27070af496cb632641/CNX_Chem_03_01_alsulfatemass_img.jpg" src="http://cnx.org/resources/69320dd9501e62acfadfea27070af496cb632641/CNX_Chem_03_01_alsulfatemass_img.jpg"></div>

    Aluminum Sulfate (Al2(SO4)3) = 342.14g/mol (Image adopted from OpenSTAX)

    NOTE: we could have used the molar mass of sulfate that was calculated above

    \[3x96.06 + 2(26.98)= 241.14 \nonumber\]

    Answer b

    Benzene (C6H6) = 78.12g/mol

    Answer c

    Acetylene (C2H2) = 26.04g/mol

    Answer d

    Water (H2O) = 18.02g/mol

    Answer e

    Hydrogen Peroxide (H2O2) = 34.02g/mol

    Exercise \(\PageIndex{3}\)

    What is the molar mass for each of the following molecules?

    1. Sodium Bicarbonate
    2. Ammonium Nitrate
    3. Potassium Perchlorate
    4. Silver Chloride
    5. Acetic Acid
    Answer a

    Sodium Bicarbonate (NaHCO3) = 84.02g/mol

    Answer b

    Ammonium Nitrate (NH4NO3) = 80.08g/mol

    Answer c

    Potassium Perchlorate (ClKO4) = 138.54g/mol

    Answer d

    Silver Chloride (AgCl) = 143.32g/mol

    Answer e

    Acetic Acid (CH3COOH) = 60.06g/mol

    Contributors and Attributions

    Robert E. Belford (University of Arkansas Little Rock; Department of Chemistry). The breadth, depth and veracity of this work is the responsibility of Robert E. Belford, rebelford@ualr.edu. You should contact him if you have any concerns. This material has both original contributions, and content built upon prior contributions of the LibreTexts Community and other resources, including but not limited to:

    • November Palmer, Ronia Kattoum & Emily Choate (UALR)
    • Some material adapted from Paul Flowers, Klaus Theopold & Richard Langley via OpenStax (LibreText Copy section 3.1)

    This page titled 2.8: Atoms and the Mole is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Robert Belford.