8.1: Measuring Concentrations of Solutions
- Page ID
- 283929
Learning Objectives
- Define Molarity
- Differentiate between solute, solvent, and solution
- Calculate the molar concentration for solutes
- Outline the steps to make a solution of a desired concentration from a solid or aqueous solute
- Calculate the concentration of ions in a soluble ionic compound
- Perform stoichiometric calculations involving aqueous solutes
- Calculate the concentration of unknown solutes
Introduction
Up to this point we have used stoichiometry to "count" atoms, molecules and ions by measuring mass of pure substances and using molar masses to calculate the number of chemical entities (moles). Many of the reactions we have studied involve solutions, where we are interested in a solute that is dissolved in a solvent, and we can not measure the mass of the solute independent of the solvent. We also need to realize that many chemical reactions require the reactants to be mobile, where they can bump into each other, and this can occur when they are dissolved in a solvent. So it is very important that we can count chemical entities when the entity of interest is a solute dissolved in a solvent, and in which case we measure the mass of volume of the solution as a whole (solvent plus all solutes) of which volume is typically the easiest to measure.
Concentration of a Solute
There are two basic ways of reporting the concentration of a solute in a solvent, by reporting the mass of solute in a given volume, or the number of moles of solute in a given volume. These are effectively conversion factors that define the equivalent mass or moles of a solute to the volume of the solution.
- Mass Concentration: has typical units of g/L \[\frac{mass\: solute}{vol \: solution}=\frac{m(g))}{V(L))}\]
- Mole Concentration (Molarity): has units of mol/L or M . You can consider M as a shorthand notation for mol/L.\[\frac{moles\: solute}{vol \: solution}=\frac{n(moles))}{V(L))} = M \; or \; (mol/L)\]
So a 3.0M solution of sucrose has 3.0 mole of sucrose per liter
How do we convert between mass and mole based concentration?
Simply by multiplying or dividing by the molar mass (g/mol). If you know the g/L, you simply divide by the molar mass, and if you know the moles/L and want the mass/L, you multiply by the molar mass (just use the molar mass as an equivalence statement).
How do we "count" solute molecules and ions?
By measuring the volume and knowing the molarity. This is analagous to measuring the mass and knowing the molar mass for a pure substance.
\[n(moles)=M(\frac{mol}{L})(V(L)) \\ n=MV\]
This can be contrasted to how we "count" chemical entities that are pure solids.
\[n(moles)=\frac{m(g)}{molar \; mass (\frac{g}{mol})} \\ n=\frac{m}{fw}\]
Making a Solution with a Solid Solute.
Step 1: Calculate Mass of solute needed for desired volume
Step 2: Quantitatively Transfer Mass to Volumetric Flask
Step 3: Dilute to volume with solvent, ensuring that all of the solid has dissolved.
Making 500.0 mL of 0.500 M Copper(II)Sulfate
Step 1: Calculate Mass CuSO4(s) needed.
\[0.5000L\left (\frac{0.500molCuSO_{4}}{L} \right )\left ( \frac{159.6gCuSO_{4}}{mol} \right )=39.9gCuSO_{4}\]
Step 2: Weight 39.9g CuSO4(s) and quantitatively transfer to 500 mL graduated cylinder (which is calibrated to 500.0 mL), being sure all the salt is transferred.
Step 3: Fill half way and mix, then dilute to volume. Make sure all the solute is dissolved, and recheck that solution level is at bottom of meniscus.
Exercise \(\PageIndex{1}\)
What is the molarity of a solution made when 66.2 g of C6H12O6 are dissolved to make 235 mL of solution?
- Answer
-
1.57 M C6H12O6
Why can't you just add 500.0mL of water to 39.9 g CuSO4 to make 500.0 mL of 0.500M solution?
First, this is not taking into account the volume of the solute, and second, there is usually a change in volume when you dissolve a solute into a solvent, and in the case of ionic compounds this is a contraction.
Exercise \(\PageIndex{2}\)
Using concentration as a conversion factor, perform the following calculation.
- How many liters of 0.0444 M CH2O are needed to obtain 0.0773 mol of CH2O?
- What mass of solute is present in 1.08 L of 0.0578 M H2SO4?
- What volume of 1.50 M HCl solution contains 10.0 g of hydrogen chloride?
- Answer a
-
1.74 L
\[0.0773mol \;CH_2O\left ( \frac{L \; solution}{0.0444mol \; CH_2O} \right )=1.7409L\]
- Answer b
-
6.12 g
\[1.08L \;solution\left ( \frac{0.0578mol \; H_2SO_4}{L \; solution} \right )\left ( \frac{98.08g \; H_2SO_4}{mol} \right )=6.122546 g \;H_2SO_4\]
- Answer c
-
183 mL or 0.183L
\[10.0g \;HCl\left ( \frac{mol \; HCl}{36.46g} \right )\left ( \frac{L \; solution}{1.5mol \; HCl} \right )=0.182849L\]
Ion Concentrations in Solution
When an ionic compound dissolves it breaks up into its ions.
(NH4)2Cr2O7(aq) --> 2NH4+(aq) + Cr2O7(aq)
Dissolving 252.07 grams of ammonium dichromate (fw = 252.07 g/mol) results in a solution that is 1M ammonium dichromate, but when an ionic salt dissolves, it breaks up into ions, and so what you really have is a solution that is 2 M ammonium ion (NH4+) and 1 M in dichromate ion (Cr2O7+2)
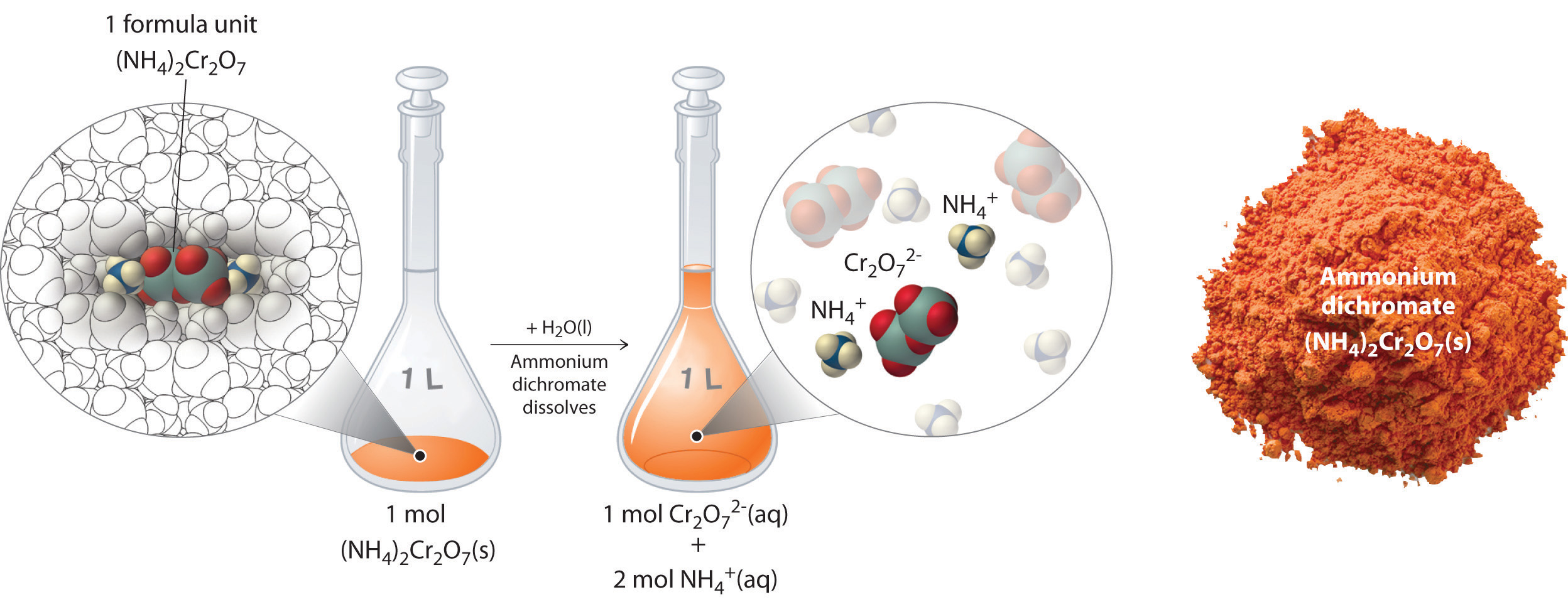
Dissolution of 1 mol of an Ionic Compound. In this case, dissolving 1 mol of (NH4)2Cr2O7 produces a solution that contains 1 mol of Cr2O72− ions and 2 mol of NH4+ ions. (Water molecules are omitted from a molecular view of the solution for clarity.)
Example \(\PageIndex{1}\) Solution Concentration of Iron(II)chloride
Water is added to 2.16 g of the ionic compound ferrous chloride to make a solution with a total volume of 100.0 mL. Express the concentration of the salt solution, and that of its ions.
1. What is the salt concentration?
2. What are the ion concentrations?
Solution
Video \(\PageIndex{1}\) goes over this calculation.
Ans: 0.170M FeCl2(aq)
0.170M Fe+2(aq)
0.340M Cl-(aq)
Yes, there are three answers! (that of the salt, and of the ions)
Video \(\PageIndex{1}\): 3'36" YouTube calculating the concentration of a Ferrous Chloride in example \(\PageIndex{1}\).
Exercise \(\PageIndex{3}\)
You have a 1.50 M solution of Na2CO3. What is the concentration of:
A) sodium ions?
B) carbonate ions?
C) total ions?
- Answer
-
A) [Na+] = 3.00 M
B) [CO3-2]= 1.50 M
C) [Na+] + [CO3 -2] = 4.50 M ; or you can choose think for every 1 mole of Na2CO3, there are 3 moles of ions (identify of the ions is irrelevant).
Preparing Solutions with Stock Concentrated Solutions (Dilution).
Many stockroom reagents come as concentrated solutions that can easily be diluted to a desired concentration by adding solvent. Adding a solvent does not change the moles of solute (n), so
ninitial = nfinal
ni = nf
MiVi = MfVf
Step 1: Calculate initial volume of stock
Step 2: Transfer to volumetric flask with a volumetric pipette
Step 3: Dilute to Volume
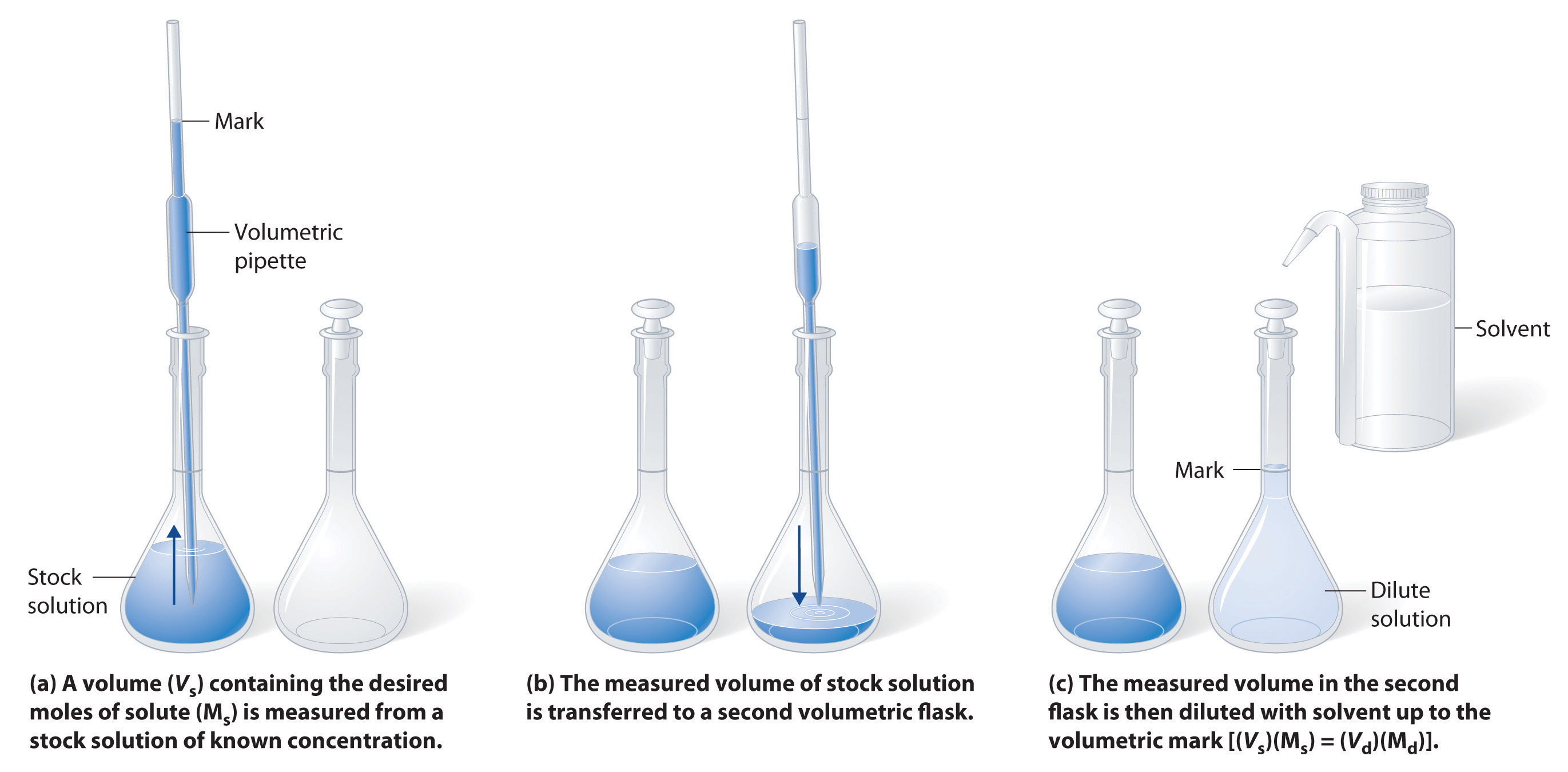
Example \(\PageIndex{2}\)
How do you make 500.0 ml of 0.70M HCl solution from stock 11.6 M HCl?
Solution
Step 1: Calculate initial volume of 11.6 M hydrochloric acid needed.
\[M_{i}V_{i}=M_{F}V_{F}\]
\[V_{i}=V_{f}\left ( \frac{M_{f}}{M_{i}} \right )=500.0mL\left ( \frac{0.70M}{11.6M} \right )=30.2mL\]
Step 2: Quantitatively transfer this volume to a 500 mL volumetric flask (this has 4 significant Figures, that is, it is calibrated to 500.0 mL)
Step 3: Dilute with water to mark
Exercise \(\PageIndex{3}\)
What is the concentration of an HCl solution if 598 mL of 0.778 M HCl is diluted to 1.00 L?
- Answer
-
\[M_{i}V_{i}=M_{F}V_{F}\nonumber\]
\[M_{f}=M_{i}\left ( \frac{V_{i}}{V_{f}} \right )=0.778 M \left ( \frac{0.0598 L }{1.00 L} \right )=0.465 M \nonumber\]
Contributors and Attributions
Robert E. Belford (University of Arkansas Little Rock; Department of Chemistry). The breadth, depth and veracity of this work is the responsibility of Robert E. Belford, rebelford@ualr.edu. You should contact him if you have any concerns. This material has both original contributions, and content built upon prior contributions of the LibreTexts Community and other resources, including but not limited to:
- November Palmer & Ronia Kattoum (UALR)
- anonymous

