6.5: Molecular Formulas

Last updated
Save as PDF

Page ID: 282802

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

learning objectives

Distinguish between empirical formula and molecular formula
Determine empirical formula and molecular formula using percent composition
Determine empirical formula and molecular formula using mass data

Introduction

Empirical measurements are based on a measurable (empirical) quantity like mass. Knowing the mass of each element in a compound we can determine its formula. There are two types of formulas, empirical and molecular.

Empirical Formula: Lowest whole number ratio of the elements in a compound

Molecular Formula: Actual whole number ratio of the elements in a compound.

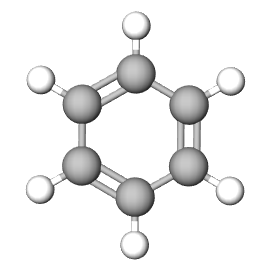
The Empirical formula is the lowest whole number ratio of the elements in a compound. In (section 2.10), we discovered that benzene and acetylene have the same mass percent composition, and thus it is logical that they have the same ratio of elements to each other, that is, they have the same empirical formula.

Compound	Acetylene	benzene	NaCl
Structure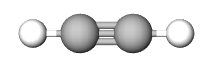
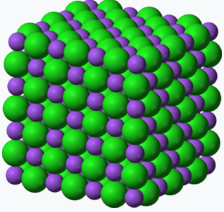Empirical Formula	CH	CH	NaCl
Molecular Formula	C₂H₂	C₆H₆	not a molecule (use NaCl)

Figure \(\PageIndex{1}\): Empirical and molecular formulas of several simple compounds.

Molecular Formula

To calculate the molecular formula we need additional information beyond that of the mass or mass percent composition, we need to know the molar mass of the substance. There are many experimental ways that can be determined, and we will learn some as the semester proceeds. The mass spectrometer that we used to determine the isotopic composition in section 2.3 of this Chapter could be used to determine the molar mass of many unknowns. But there are other techniques, and at this point in the semester, the molar mass will be treated as a given.

The empirical formula represents the lowest whole number ratio of the elements in a molecule while the molecular formula represents the actual formula of the molecule. So the molecular formula must be an integer multiple of the empircal formula, that is it is n times larger where n=1 or 2 or 3 or.... but it is an integer. This gives the following relationship

\[\text{[Molecular Formula = n([Empirical Formula)]}\]

then if we have one mole

\[\text{[Molecular Weight = n([Empirical Weight)]}\]

\[n=\frac{\text{[Molecular Weight]}}{\text{[Empirical Weight]}}\]

So you calculate the Empirical formula as above, then determine the weight of one mole, divide that into the molar mass, and that tells you how many times it is bigger, and then multiple the emprical formula by that number.

Let's compare Benzene to acetylene. In video 2.10.2 (section 2.10.2) we saw that benzene and acetylene had the same mass % composition and in exercise 2.11.3 we say they had the same empirical formula

Table \(\PageIndex{1}\): data setup for calculating molecular formula for empirical formula and molar mass for benzene and acetylene
name:	Benzene	Acetylene
Formula Weight	78.12g/mol	26.04g/mol
Empirical Formula	CH	CH
Empirical Formula Weight	13.017	13.017
n=\(\frac{\text{[Molecular Weight]}}{\text{[Empirical Weight]}}\)	\(\frac{78.12}{13.017}=6\)	\(\frac{26.04}{13.017}=2\)
Formula = n times empirical formula	6(CH) = C₆H₆	2(CH) = C₂H₂

Calculating Molecular Formulas

Example \(\PageIndex{2}\)

A certain compound was found to contain 67.6% C, 22.5% O, and 9.9% H. If the molecular weight of the compound was found to be approximately 142 g/mol, what is the correct molecular formula for the compound?

Solution

C₄H₇O has a empirical weight of

(4)(12.01) + (7)(1.007) + (16.00) = 71.09g/mol

\[\left ( \frac{142g/mol}{71.09g/mol} \right )= 2\]

multiply the coefficients by 2

C₈H₁₄O₂

Test Yourself

Homework: Section 6.5

Graded Assignment: Section 6.5

Exercise \(\PageIndex{4}\): Molecular formula

Calculate the molecular formula for the following

A compound has an empirical formula of C₂HF has a molar mass of 132.06 g/mol.
200.0 g sample of an acid with a molar mass of 616.73g/mol contains 171.36 g of carbon, 18.18g of nitrogen and the rest is hydrogen.
Strychine has a molar mass of 334 g/mol and percent composition of 75.42%C, 6.63%H and 8.38%N and the rest oxygen.

Answer a: C₆H₃F₃

Answer b: C₄₄N₄H₃₂

Answer c: C₂₁N₂H₂₂O₂

Contributors and Attributions

Robert E. Belford (University of Arkansas Little Rock; Department of Chemistry). The breadth, depth and veracity of this work is the responsibility of Robert E. Belford, rebelford@ualr.edu. You should contact him if you have any concerns. This material has both original contributions, and content built upon prior contributions of the LibreTexts Community and other resources, including but not limited to:

November Palmer & Emily Choate (UALR)
Ronia Kattoum (Learning Objectives)