1.2: Mathematics and Scientific Communication
- Page ID
- 211895
Introduction
Before covering any chemistry it is important to understand the difference between algebra and arithmetic, and how they are applied to scientific theory. In this activity we will jump to material that will be covered later in the semester, like the First Law of Thermodynamics, and our goal is not to solve a thermodynamic problem, but to understand the difference between an algebraic equation and an arithmetic calculation. That is, to the scientist algebra is a language that can state knowledge through the use of variables that have physical meaning and significance, and just like a sentence in the English language, it can be read and understood by someone who knows the science. The algebraic equation (sentence) can mathematically be solved for a specific variable whose value can be arithmetically determined if the values of the other variables are known, but once you substitute that numerical values into the variables, it can no longer be read like a sentence in the English language. Figure \(\PageIndex{1}\) shows a flow chart that relates these where you develop an algebraic equation based on scientific theory and law, solve that for the value you seek and then substitute in the numbers to produce the answer you desire.
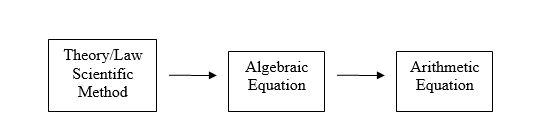
Lets apply Figure \(\PageIndex{1}\) to a scientific problem that we will need to be able to solve before this semester is over. We could ask the following question in English.
Example \(\PageIndex{1}\)
What is the final temperature if a 1 g piece of aluminum at 800 C is dropped into 1 mL of water at 200 C in a thermally isolated system?
Solution
To solve this problem we need to derive an algebraic equation from scientific theory and law. Later in this semester you will learn about the First Law of Thermodynamics, which states that the Energy of the Universe is constant, and that for an isolated system the heat lost by a hot object is the heat gained by a cold object if they are in a thermally isolated system. This can be described by the following algebraic equation, where Qh is the heat leaving the hot object (note there is a negative sign) and Qc is the heat gained by the cold object.
-Qh = Qc
But the above equation gives us no information relating this energy flow to the temperature and so as written, can not be used to solve our problem. But as we shall learn later this semester, when you add heat to a substance one of three things typically happens
- The temperature rises
- A phase change occurs
- A chemical reaction occurs
For a system at constant phase where there is no reaction occurring (the iron does not heat the water so much that it boils or breaks into hydrogen and oxygen), we can relate the heat transferred and temperature change to a property of the matter called its heat capacitance, which can be expressed as
\[Q=C \Delta T \]
or
\[Q=mc\Delta T \]
where for aluminum cAl= 0.902J/(g-K) and for water cWater= 4.184J/(g-K)
substituting eq into eq gives
-mhch(TF-TH) = mccc(TF-Tc)
Which can be solved for the final Temperature
\[T_F=\frac{m_Hc_HT_H+m_cc_cT_c}{m_Hc_H+m_cc_c} \]
Once this is done, you plug in your numbers and do the arithmetic.
\[T_F=\frac{(1.00g)(0.902\frac{J}{g\cdot ^{o}C})80.0^{o}C+(1.00ml)(\frac{1.00g}{1.00ml})(4.184\frac{J}{g\cdot ^{o}C})20.0^{o}C}{(1.00g)(0.902\frac{J}{g\cdot ^{o}C})+(1.00ml)(\frac{1.00g}{1.00ml})(4.184\frac{J}{g\cdot ^{o}C})} =30.0^o C\]
or worse, you could do the math as a pure arithmetic problem
\[T_F=\frac{(1.00)(0.902)80.0+(1.00)(\frac{1.00}{1.00})(4.184)20.0}{(1.00)(0.902)+(1.00ml)(\frac{1.00}{1.00})(4.184)} =30.0^o C\]
The important message is you can read eq. _____ but can not read eq. ____. That is, eq. is an algebraic equation, and a scientist who has passed freshmen chemistry can read the equation and identify if there was a mathematical mistake when it was solved, where as eq. is just an arithmetic operation where you plug the numbers into a calculator and come up with an answer.
Can you see another potential issue with eq.____? There are no units, and you should always include units when you convert you algebraic equations to arithmetic ones, as the units should cancel in a manner where the answer has the same units on both sides of the equations (if you are solving for temperature, your answer needs the units of temperature or you made a mistake.
IMPORTANT: PARTIAL CREDIT
in this class
WILL ONLY BE GIVEN IF THE ALGEBRAIC EQUATIONS ARE SHOWN,
and when a problem states
"SHOW CALCULATIONS"
you must show both the
algebraic and the arithmetic calculations.
This is very important and a very common mistake that students make. They solve the arithmetic problems and not the algebraic, and the sooner you learn to solve the algebra, and then do the arithmetic, the better off you will be. That is the purpose of this example, and anyone who knows chemistry can read eq (), and see if there is a mistake, but eq() can not be read, it is just a bunch of numbers, that could mean anything.


