11.6: Nanoscale Metal Particles
- Last updated
- Save as PDF
- Page ID
- 226769

Nanoscale metal particles have been the subject of intense research over the past 20 years, especially because of their unusual optical, magnetic, and catalytic properties. The synthesis of metal nanocrystals in various shapes has become increasingly sophisticated and rational, like the synthesis of semiconductor nanocrystals described above. By controlling the separate phases of nucleation and growth, and by using ligands that cap specific crystal faces during growth, it is possible to make metal nanocrystals of uniform size in a variety of interesting and useful shapes including cubes, truncated cubes, octahedra, triangular prisms, and high aspect ratio rods. By exploiting displacement reactions that replace one metal with another, complex hollow shapes such as nanocages (as shown at the left) can be made starting with other shapes. In this case, solid silver nanocubes are transformed to gold nanocages.
|
Five-fold twinning in a gold nanoparticle |
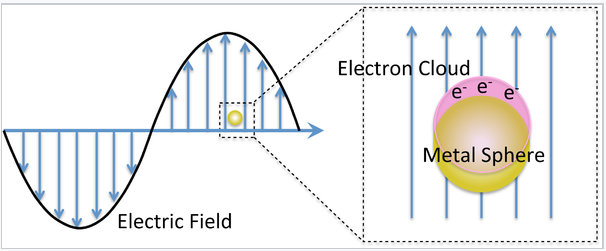
The interesting optical properties of nanocrystalline Au, Ag, Cu, and a number of other metals, derive from the collective oscillation of their valence electrons, a phenomenon known as plasmon resonance. Remember that in these metals, the electron mean free path is long (about 100 times larger than the size of the atoms), so the valence electrons feel only the average positive charge of the atomic cores as they zoom around the crystal. Light impinging on the metal acts as an oscillating electric field, pushing and pulling on the valence electrons at the characteristic frequency of the light wave. The situation is very much like a pendulum or a weight on a spring. The electrons, pushed away from their equilibrium positions, feel a restoring force that is proportional to their displacement. Their motion can be described by Hooke's Law:
\[F = kx\]
where the spring constant k determines the "stiffness" of the spring. In the case of the plasmon resonance, k is proportional to the number density of valence electrons n, and the square of the electronic charge e:
\[k = \frac{ne^{2}}{\varepsilon_{0}}\]
The resonant frequency of the plasma oscillation is given by:
\[\omega_{p} = (\frac{k}{m})^{\frac{1}{2}} = (\frac{ne^{2}}{m_{e}\varepsilon_{0}}^{\frac{1}{2}}\]
where me is the electron mass. For most metals, the plasmon resonance is in the ultraviolet part of the spectrum, but for a few metals like Au, Ag, and Cu it is in the visible.
|
The Lycurgus cup (4th century Roman glass) derives its unique coloration from noble metal nanoparticles. The cup is red in transmitted light and green in scattered (reflected) light. |
For metal particles that are much smaller than the wavelength of light, this effect is called the localized surface plasmon resonance, or LSPR. There are three important consequences of the LSPR effect:
- The local electric field of the incoming light wave is greatly enhanced at the particle surface. This gives rise to huge enhancement factors in optical processes such as Raman scattering and fluorescence. Thus, certain analytical spectroscopic techniques are greatly enhanced by LSPR.
- Near the plasmon resonance frequency, metal nanocrystals absorb and scatter light very strongly. This makes them brightly reflective, and the strong light absorption can be exploited for light-induced local heating. These properties are being applied in medical diagnostics and therapy, e.g., for detection and photothermal destruction of cancer cells. By adjusting the size and shape of the gold nanoparticles, which are more stable than Ag and Cu in biological media, the plasmon frequency can be tuned to the tissue-transparent near-IR region of the spectrum between 700 and 900 nm. Small quantities of plasmonic Ag and Au particles also make brightly colored and strongly scattering pigments, e.g. in stained glass as shown above at the right.
- The plasmon frequency is sensitive to the refractive index of the particle's surroundings, i.e., its chemical environment. This makes metal nanoparticles of special interest for sensing and biosensing applications.
|
The colors of plasmonic gold nanoparticles depend on their size and shape. |
Theory of light scattering and absorption by metal nanoparticles
The valence electrons in metal nanoparticles oscillate in the electric field of a light wave. While the nature of these oscillations is somewhat complex in metal particles that are non-spherical, the theory for spherical particles is relatively simple and in fact was worked out over 100 years ago by German physicist Gustav Mie.
|
|
Mie considered the interaction of a spherical particle with a uniform electric field, E, oscillating at angular frequency ω (= 2π f). This is a good approximation when the particle diameter is much smaller than the wavelength of light, as shown on the left. The particle is embedded in a uniform, insulating material (e.g. a solvent) that has a dielectric constant εdiel. For insulators, εdiel is a positive real number.
The dielectric constant ε of a metal is actually a complex number:
\[\varepsilon = \varepsilon^{'} + i \varepsilon^{"}\]
Here the real part, ε', is related to the refraction of light, and the imaginary part, ε", is related to light absorption. Both ε' and ε" are dependent on the frequency of the light. For metals near the plasmon resonance frequency, ε' is typically a negative number.
The cross-section for absorption of the light wave by the particle is:
\[\sigma_{absorption} = \frac{9 \omega}{c} \epsilon^{\frac{3}{2}}_{diel} V \frac{\epsilon^{"}_{metal}}{(\epsilon^{'}_{metal} + 2 \epsilon_{diel})^{2} + (\epsilon^{"}_{metal})^{2}}\]
and the cross-section for scattering is:
\[ \sigma_{scattering} = \frac{3}{2\pi} (\frac{\omega^{4}}{c}) \epsilon^{2}_{diel} V^{2} \frac{(\epsilon^{'}_{metal} - \epsilon_{diel})^{2} + (\epsilon^{"}_{metal})^{2}}{(\epsilon^{'}_{metal} + 2 \epsilon_{diel})^{2} + (\epsilon^{"}_{metal})^{2}}\]
The sum of these two is the cross-section for extinction:
\[\sigma_{extinction} = \sigma_{absorption} + \sigma_{scattering}\]
These cross-sections become large when the (ε'metal + 2εdiel) term in the denominator becomes small. This occurs when
\[\epsilon^{'}_{metal} \simeq -2\epsilon_{diel}\]
For 15 nm diameter gold nanoparticles in water, this happens at about 580 nm, resulting in the characteristic wine-red color of colloidal gold solutions. Changing the solution environment (e.g., by adsorbing a molecule onto the gold surface) changes εdiel and thus alters the color slightly.
It is important to note that the cross-section for scattering is proportional to the square of the volume of the particle, V2, whereas the absorption is proportional to V. This means that very small gold particles (< 5 nm) are strongly absorbing but not strongly scattering. Larger particles (>30 nm) scatter light very strongly. Depending on the application, therefore, we choose larger or smaller particles.
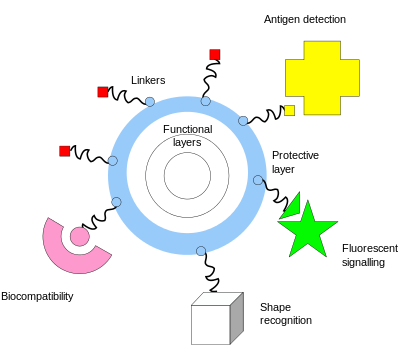
One of the key complementary properties of noble metal nanoparticles that is important to their use in biomedicine is the ease with which they can be covalently conjugated with polymers or small molecules, typically via thiol or amine bonds at their surface. This imparts biological recognition properties to the particles that enables them to bind to specific biomolecular targets. The figure at the left illustrates some of the functionality that can be imparted to nanoparticles through surface functionalization.
Functionalization of gold nanoparticles with thiol-terminated single-stranded DNA was the basis of one of the first nanoparticle sensors, developed by the Mirkin group at Northwestern University. DNA-coated nanoparticles have the characterstic wine-red plasmonic color of spherical nano-gold. However, when these particles are linked together by a complementary DNA strand, the resonance frequency shifs, resulting in a blue color. This color change, illustrated in the figure at the right, provides a "litmus test" for the presence of the target DNA sequence.[10] "Melting" of the DNA - heating it to the temperature at which double stranded DNA dissociates to make single strands - reverses the color change. The DNA hybridization/melting transition is highly cooperative because of the aggregation of many gold particles, so the transition temperature is very sharp. With proper temperature control, the color change can be sensitive to a single base mismatch in the target DNA that is detected by this method.
|
Aggregation of Au nanoparticles (in this case by adding salt to a colloidal solution) causes a color change from wine red (left) to blue (right). Photo credit: George Lisensky, Beloit College |
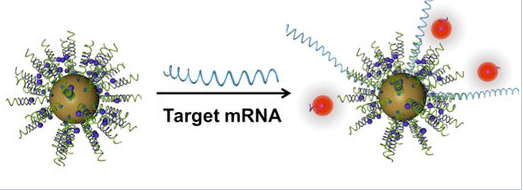
Subsequent research has developed sophisticated diagnostic and therapeutic ("theranostic") applications for these spherical nucleic acid[11] particles. These particles easily penetrate cell membranes and can report on the chemistry happening inside living cells.
|
General schematic of nanoflare-based detection. |
An important property of gold nanoparticles in these applications is their ability to quench the fluorescence of reporter molecules that are near their surface. Nucleic acid strands that contain a hairpin loop can position fluorescent molecules near the gold surface, where their fluorescence is turned off by nanoparticle quenching. Hybridization of these sequences to target RNA or DNA causes the fluorescence to turn on by moving the fluorescent molecule away from the nanoparticle surface. These so called "nanoflares" can thus signal the up- or down-regulation of specific genes inside cells. Nanoflares are the basis of the Verigene System, developed and commercialized by Nanosphere, Inc. to detect markers for infectious diseases and cancers.