10.7: Atomic Orbitals and Magnetism
- Last updated
- Save as PDF
- Page ID
- 226721
The MO picture we developed in Section 6.4 helps us rationalize the electrical conductivity of Na (3s1), but what about Mg, which (as an atom in the gas phase) has a 3s2 electronic configuration? The two valence electrons are spin-paired in atomic Mg, as they are in the helium atom (1s2). When the 3s orbitals of Mg combine to form a band, we would expect the band to be completely filled, since Mg has two electrons per orbital. By this reasoning, solid Mg should be an insulator. But Mg has all the properties of a metal: high electrical and thermal conductivity, metallic luster, malleability, etc. In this case the 3s and 3p bands are sufficiently broad (because of strong orbital overlap between Mg atoms) that they form a continuous band. This band, which contains a total of four orbitals (one 3s and three 3p) per atom, is only partially filled by the two valence electrons.
|
Mg crystals |
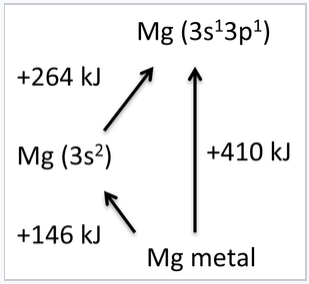
Another way to think about this is to consider the hybridization of the 3s and 3p electrons in Mg. Hybridization requires promotion from the 3s23p0 ground state of an Mg atom to a 3s13p1 excited state. The promotion energy (+264 kJ/mol) is more than offset by the bonding energy (-410 kJ/mol), the energy released when gaseous atoms in the excited state condense to form the metallic solid. The heat of vaporization, or the cohesive energy of a metal, is the difference between the bonding energy and the promotion energy. Experimentally, we can measure the vaporization energy (+146 kJ/mol) and the promotion energy and use them to calculate the bonding energy. From this we learn that each s or p electron is worth about 200 kJ/mol in bonding energy. The concepts of promotion energy and bonding energy are very useful in rationalizing periodic trends in the bond strengths and magnetic properties of metals, which are described below.
|
The cohesive energy of Mg metal is the difference between the bonding and promotion energies. The ground state of a gas phase Mg atom is [Ar]3s2, but it can be promoted to the [Ar]3s13p1 state, which is 264 kJ/mol above the ground state. Mg uses two electrons per atom to make bonds, and the sublimation energy of the metal is 146 kJ/mol. |
Periodic trends in d-electron bonding
While electrons in s and p orbitals tend to form strong bonds, d-electron bonds can be strong or weak. There are two important periodic trends that are related to orbital size and orbital overlap. As we move across the periodic table ( Sc - Ti - V - Cr - Fe ), the d orbitals contract because of increasing nuclear charge. Moving down the periodic table ( V - Nb - Ta ), the d orbitals expand because of the increase in principal quantum number. These trends explain the distinct behavior of the 3d elements relative to those in the 4d and 5d series. In the 3d series, the contraction of orbitals affects the ability of the d electrons to contribute to bonding. Past V in the first row of the transition metals, the 3d electrons become much less effective in bonding because they overlap weakly with their neighbors. Weak overlap of 3d orbitals gives narrow d-bands and results in the emergence of magnetic properties as discussed below.
|
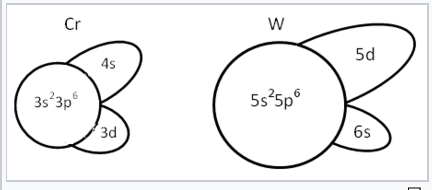
Schematic representation of the sizes of different orbitals of Cr and W. In the first transition series, shielding of the 3d orbitals is poor. Therefore the 4s and 4p orbitals are more effective in bonding than the 3d. In the third transition series, the situation is reversed. The increased nuclear charge is felt most strongly by the 6s, which takes on the character of an inert electron pair. The 5d orbitals are well shielded by the complete n=4 shell so they have good orbital overlap with neighboring atoms. |
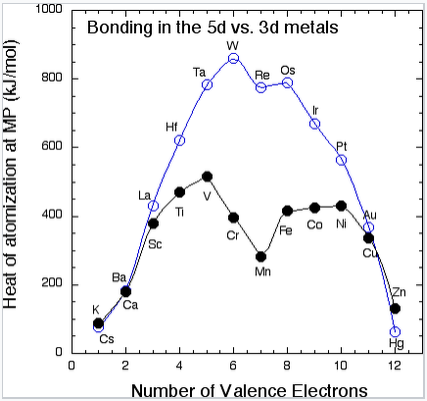
In the 4d and 5d series, a plot of cohesive energy vs. number of valence electrons (below left) has a "volcano" shape that is peaked at the elements Mo and W (5s14d5 and 6s15d5, respectively). The number of bonding electrons, and therefore the bonding energy, increases steadily going from Rb to Mo in the 4d series, and from Cs to W in the 5d series. Mo and W have the most bonding energy because they can use all six of their valence electrons in bonding without promotion. Elements past Mo and W have more d electrons, but some of them are spin paired and so some promotion energy is needed to prepare these electrons for bonding. For example, Pt metal must be promoted from the 6s15d9 atomic ground state to 6s15d76p2 in order to make six bonds per atom, and the energy cost of promoting electrons from the 5d to the 6p orbitals is reflected in the net bonding energy. Because of their strong bonding energy, elements in the middle of the 4d and 5d series have very high melting points. We do not see magnetism in the 4d or 5d metals or their alloys because orbital overlap is strong and the bonding energy exceeds the electron pairing energy.
|
The heat of vaporization (the cohesive energy) of metals in the 3d and 5d series, measured at the melting point of the metal. |
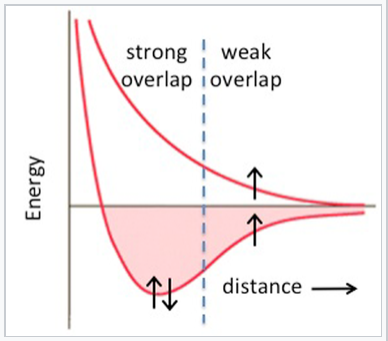
The 3d elements (Sc through Zn) are distinctly different from the 4d and 5d elements in their bonding (and consequently in their magnetic properties). In the 3d series, we see the expected increase in cohesive energy going from Ca (4s2) to Sc (4s23d1) to Ti (4s23d2) to V (4s23d3), but then something very odd happens. The 3d series has a "crater" in the cohesive energy plot where there was a peak in the 5d series. The cohesive energy actually decreases going from V to Mn, even though the number of valence electrons is increasing. We can explain this effect by remembering that the 3d orbitals are progressively contracting as more protons are added to the nucleus. For elements beyond V, the orbital overlap is so poor that the 3d electrons are no longer effective in bonding, and the valence electrons begin to unpair. At this point the elements become magnetic. Depending on the way the spins order, metals and alloys in this part of the periodic table can be ferromagnetic (spins on neighboring atoms aligned parallel, as in the case of Fe or Ni) or antiferromagnetic (spins on neighboring atoms antiparallel, as in the case of Mn). We have seen the trade-off between orbital overlap and magnetism before (in Chapter 5) in the context of paramagnetic transition metal complexes. It is worth recalling that this behavior is predicted in the energy vs. distance diagram of the hydrogen atom (from Chapter 2). At short interatomic distances (or with strong overlap between atomic orbitals), the spins of the electrons pair and a bond is formed. Unpairing the electrons becomes favorable at larger interatomic distances where the overlap between orbitals is poor.
|
With strong overlap between orbitals of neighboring atoms, the bonding energy exceeds the pairing energy and electrons spin-pair. With weaker overlap, bonding is weak and spins unpair, resulting in magnetic behavior. |
Interestingly, many alloys of the 4f elements (the lanthanides) are also magnetic because the 4f orbitals, like the 3d orbitals, are poorly shielded from the nuclear charge and are ineffective in bonding. Strong permanent magnets often contain alloys of Nd, Sm, or Y, usually with magnetic 3d elements such as Fe and Co.
Because the 4f orbitals are contracted and not very effective in bonding, other physical properties of the lanthanides can also be affected. For example, it has been proposed that oxides of the 4f elements have weak surface interactions with polar molecules such as water because of f-orbital contraction. Experimentally, CeO2, Er2O3, and Ho2O3 are observed to be hydrophobic, whereas main group and early transition metal oxides (e.g., Al2O3, SiO2, TiO2) are quite hydrophilic.[1]
Late transition metal alloys
Although the bonding in the 5d series follows a "normal" volcano plot, the situation is a bit more complex for alloys of Re, Os, Ir, Pt, and Au. There is strong overlap between the 5d orbitals, but because these elements contain more than five d-electrons per atom, they cannot make as many bonds as 4d or 5d elements with half-filled d-shells such as Mo or W. This progressive filling of the d-band explains the steady decrease in bonding energy going from Os to Au. Pt and Au are both soft metals with relatively low heats of vaporization. However, these metals (especially Ir, Pt, and Au) can combine with early transition metals to form stable alloys with very negative heats of formation and high melting points. For example, ZrC and Pt react to form a number of stable alloys (ZrPt, Zr9Pt11, Zr3Pt4, ZrPt3)[2] plus carbon. This reactivity is unusual because we normally think of Pt as a "noble" (i.e., unreactive) metal, and because ZrC is a very stable, refractory metal carbide. The favorable combination of early and late transition metals has been interpreted as arising from a d-electron "acid-base" interaction.[3] For example, in HfPt3, Hf is the "acid" with an electron configuration of 6s25d2, while Pt is the "base" with the electron configuration of 6s15d9. They combine to create a stable "salt" product with a filled 5d electron configuration without promoting any electrons to higher orbitals. The implication is that Pt donates d-electrons to the "d-acid," Zr or Hf. However, electronic structure calculations on model compounds show that much of the bonding energy in ZrPt and ZrPt3 arises from electron transfer from Zr to Pt (not the other way around) and the polarity of the resulting metal-metal bonds.[4] Regardless of the source of their stability, some early-late transition metal alloys are of particular interest for use in catalysis. For example, the alloy ScPt3 is a good catalyst for oxygen reduction in fuel cells. Even though Sc is an active metal that is easily oxidized, it is stabilized in the aqueous acid environment of the fuel cell by its strong interaction with Pt.[5]
Filling of the 3d and 4s,4p bands
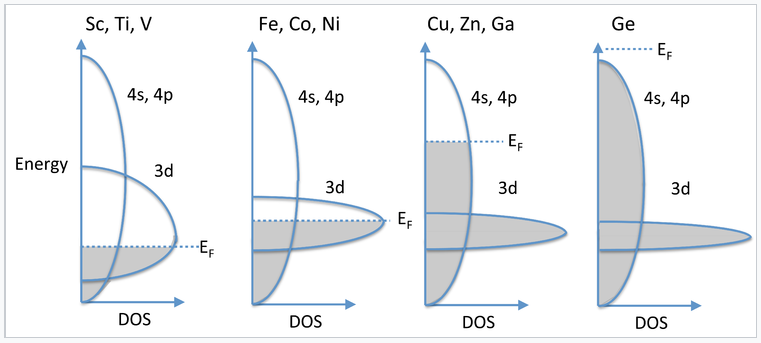
In the 3d series, we see magnetic behavior for elements and alloys between Cr and Ni. Past Ni, the elements (Cu, Zn, Ga,...) are no longer magnetic and they are very good electrical conductors, implying that their valence electrons are highly delocalized. We can understand this behavior by considering the overlap of 4s, 4p, and 3d orbitals, all of which are close in energy. The 4s and 4p have strong overlap and form a broad, continuous band. On the other hand, the 3d electrons are contracted and form a relatively narrow band. Progressing from the early 3d elements (Sc, Ti, V), we begin to fill the 3d orbitals, which are not yet so contracted that they cannot contribute to bonding. Thus, the valence electrons in Sc, Ti, and V are all spin-paired, except for a small number near the Fermi level that give rise to a weak Pauli paramagnetism. Moving across the 3d series to the magnetic elements (Fe, Co, Ni), the d-orbitals are now so contracted that their electrons unpair and we see cooperative ordering of spins (ferromagnetism and antiferromagnetism). Referring to the band diagram at the right, the 3d band is only partially filled and the Fermi level cuts through it. For Cu, Zn, and Ga, the 3d orbitals are even more contracted and the 3d band is thus more narrow, but now it is completely filled and the Fermi level is in the 4s,4p band. The strong orbital overlap in these bands results in spin pairing and a high degree of electron delocalization. Consequently, metals in this part of the periodic table (Cu, Ag) are diamagnetic and are among the best electrical conductors at room temperature. Finally, at Ge, the 4s,4p band is completely filled and the solid is a semiconductor.
|
Progressive filling of the 3d and 4s,4p bands going across the periodic table from Sc to Ge. |
Materials are classified as diamagnetic if they contain no unpaired electrons. Diamagnetic substances are very weakly repelled from an inhomogeneous magnetic field. As we learned in Chapter 5, molecules or ions that have unpaired spins are paramagnetic and are attracted to a magnet, i.e., they move towards the high field region of an inhomogeneous field. This attractive force results from the alignment of spins with the field, but in the case of paramagnetism each molecule acts independently. In metals, alloys, oxides, and other solid state compounds, the unpaired spins interact strongly with each other and can order spontaneously, resulting in the cooperative magnetic phenomena described below.