9.4: Semiconductors and Doping
- Page ID
- 226703
By the end of this section, you will be able to:
- Describe changes to the energy structure of a semiconductor due to doping
- Distinguish between an n-type and p-type semiconductor
- Describe the Hall effect and explain its significance
- Calculate the charge, drift velocity, and charge carrier number density of a semiconductor using information from a Hall effect experiment
In the preceding section, we considered only the contribution to the electric current due to electrons occupying states in the conduction band. However, moving an electron from the valence band to the conduction band leaves an unoccupied state or hole in the energy structure of the valence band, which a nearby electron can move into. As these holes are filled by other electrons, new holes are created. The electric current associated with this filling can be viewed as the collective motion of many negatively charged electrons or the motion of the positively charged electron holes.
To illustrate, consider the one-dimensional lattice in Figure \(\PageIndex{1}\). Assume that each lattice atom contributes one valence electron to the current. As the hole on the right is filled, this hole moves to the left. The current can be interpreted as the flow of positive charge to the left. The density of holes, or the number of holes per unit volume, is represented by p. Each electron that transitions into the conduction band leaves behind a hole. If the conduction band is originally empty, the conduction electron density p is equal to the hole density, that is, \(n = p\).
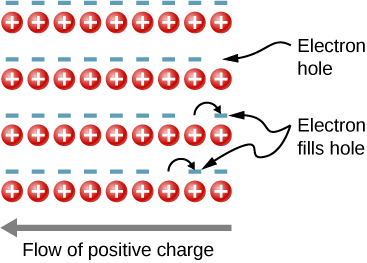 Figure \(\PageIndex{1}\): The motion of holes in a
crystal lattice. As electrons shift to the right, an electron hole
moves to the left.
Figure \(\PageIndex{1}\): The motion of holes in a
crystal lattice. As electrons shift to the right, an electron hole
moves to the left.
As mentioned, a semiconductor is a material with a filled valence band, an unfilled conduction band, and a relatively small energy gap between the bands. Excess electrons or holes can be introduced into the material by the substitution into the crystal lattice of an impurity atom, which is an atom of a slightly different valence number. This process is known as doping. For example, suppose we add an arsenic atom to a crystal of silicon (Figure \(\PageIndex{2a}\)).
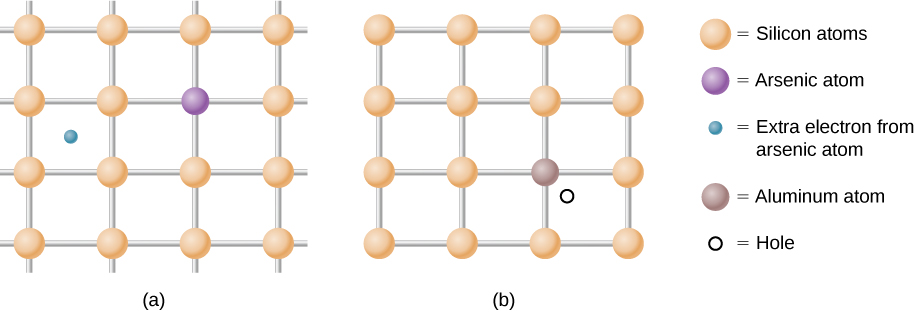 Figure \(\PageIndex{2}\): (a) A donor impurity and (b)
an acceptor impurity. The introduction to impurities and acceptors
into a semiconductor significantly changes the electronic
properties of this material.
Figure \(\PageIndex{2}\): (a) A donor impurity and (b)
an acceptor impurity. The introduction to impurities and acceptors
into a semiconductor significantly changes the electronic
properties of this material.
Arsenic has five valence electrons, whereas silicon has only four. This extra electron must therefore go into the conduction band, since there is no room in the valence band. The arsenic ion left behind has a net positive charge that weakly binds the delocalized electron. The binding is weak because the surrounding atomic lattice shields the ion’s electric field. As a result, the binding energy of the extra electron is only about 0.02 eV. In other words, the energy level of the impurity electron is in the band gap below the conduction band by 0.02 eV, a much smaller value than the energy of the gap, 1.14 eV. At room temperature, this impurity electron is easily excited into the conduction band and therefore contributes to the conductivity (Figure \(\PageIndex{3a}\)). An impurity with an extra electron is known as a donor impurity, and the doped semiconductor is called an n-type semiconductor because the primary carriers of charge (electrons) are negative.
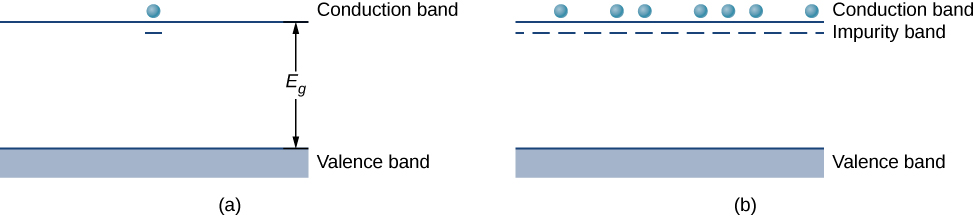 Figure \(\PageIndex{3}\): The extra electron from a
donor impurity is excited into the conduction band; (b) formation
of an impurity band in an n-type semiconductor.
Figure \(\PageIndex{3}\): The extra electron from a
donor impurity is excited into the conduction band; (b) formation
of an impurity band in an n-type semiconductor.
By adding more donor impurities, we can create an impurity band, a new energy band created by semiconductor doping, as shown in Figure \(\PageIndex{3b}\). The Fermi level is now between this band and the conduction band. At room temperature, many impurity electrons are thermally excited into the conduction band and contribute to the conductivity. Conduction can then also occur in the impurity band as vacancies are created there. Note that changes in the energy of an electron correspond to a change in the motion (velocities or kinetic energy) of these charge carriers with the semiconductor, but not the bulk motion of the semiconductor itself.
Doping can also be accomplished using impurity atoms that typically have one fewer valence electron than the semiconductor atoms. For example, Al, which has three valence electrons, can be substituted for Si, as shown in Figure \(\PageIndex{2b}\). Such an impurity is known as an acceptor impurity, and the doped semiconductor is called a p-type semiconductor, because the primary carriers of charge (holes) are positive. If a hole is treated as a positive particle weakly bound to the impurity site, then an empty electron state is created in the band gap just above the valence band. When this state is filled by an electron thermally excited from the valence band (Figure \(\PageIndex{1a}\)), a mobile hole is created in the valence band. By adding more acceptor impurities, we can create an impurity band, as shown in Figure \(\PageIndex{1b}\).
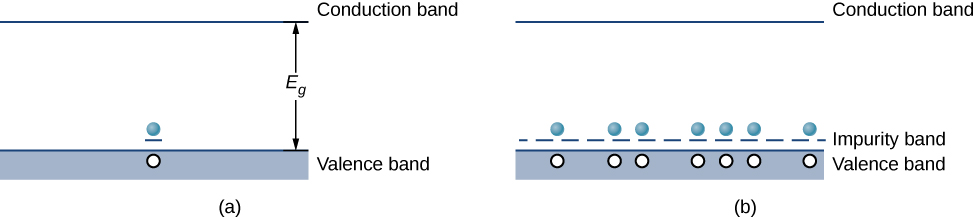 Figure \(\PageIndex{4}\): (a) An electron from the
conduction band is excited into the empty state resulting from the
acceptor impurity; (b) formation of an impurity band in a p-type
semiconductor.
Figure \(\PageIndex{4}\): (a) An electron from the
conduction band is excited into the empty state resulting from the
acceptor impurity; (b) formation of an impurity band in a p-type
semiconductor.
The electric current of a doped semiconductor can be due to the motion of a majority carrier, in which holes are contributed by an impurity atom, or due to a minority carrier, in which holes are contributed purely by thermal excitations of electrons across the energy gap. In an n-type semiconductor, majority carriers are free electrons contributed by impurity atoms, and minority carriers are free electrons produced by thermal excitations from the valence to the conduction band. In a p-type semiconductor, the majority carriers are free holes contributed by impurity atoms, and minority carriers are free holes left by the filling of states due to thermal excitation of electrons across the gap. In general, the number of majority carriers far exceeds the minority carriers. The concept of a majority and minority carriers will be used in the next section to explain the operation of diodes and transistors.
Hall Effect
In studying p- and n-type doping, it is natural to ask: Do “electron holes” really act like particles? The existence of holes in a doped p-type semiconductor is demonstrated by the Hall effect. The Hall effect is the production of a potential difference due to the motion of a conductor through an external magnetic field. A schematic of the Hall effect is shown in Figure \(\PageIndex{5a}\).
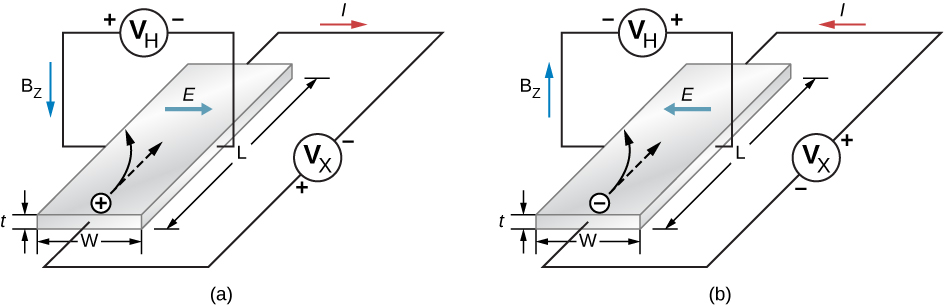 Figure \(\PageIndex{5}\): The Hall effect. (a)
Positively charged electron holes are drawn to the left by a
uniform magnetic field that points downward. An electric field is
generated to the right. (b) Negative charged electrons are drawn to
the left by a magnetic field that points up. An electric field is
generated to the left.
Figure \(\PageIndex{5}\): The Hall effect. (a)
Positively charged electron holes are drawn to the left by a
uniform magnetic field that points downward. An electric field is
generated to the right. (b) Negative charged electrons are drawn to
the left by a magnetic field that points up. An electric field is
generated to the left.
A semiconductor strip is bathed in a uniform magnetic field (which points into the paper). As the electron holes move from left to right through the semiconductor, a Lorentz force drives these charges toward the upper end of the strip. (Recall that the motion of the positively charged carriers is determined by the right-hand rule.) Positive charge continues to collect on the upper edge of the strip until the force associated with the downward electric field between the upper and lower edges of the strip (\(F_E = E_q\)) just balances the upward magnetic force (\(F_B = qvB\)). Setting these forces equal to each other, we have \(E = vB\). The voltage that develops across the strip is therefore
\[V_H = vBw, \nonumber \]
where \(V_H\) is the Hall voltage; \(v\) is the hole’s drift velocity, or average velocity of a particle that moves in a partially random fashion; B is the magnetic field strength; and w is the width of the strip. Note that the Hall voltage is transverse to the voltage that initially produces current through the material. A measurement of the sign of this voltage (or potential difference) confirms the collection of holes on the top side of the strip. The magnitude of the Hall voltage yields the drift velocity (v) of the majority carriers.
Additional information can also be extracted from the Hall voltage. Note that the electron current density (the amount of current per unit cross-sectional area of the semiconductor strip) is
\[j = nqv, \label{eq3} \]
where q is the magnitude of the charge, n is the number of charge carriers per unit volume, and v is the drift velocity. The current density is easily determined by dividing the total current by the cross-sectional area of the strip, q is charge of the hole (the magnitude of the charge of a single electron), and u is determined by Equation \ref{eq3}. Hence, the above expression for the electron current density gives the number of charge carriers per unit volume, n. A similar analysis can be conducted for negatively charged carriers in an n-type material (see Figure \(\PageIndex{5}\)).


