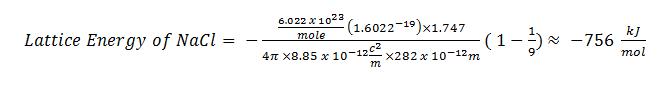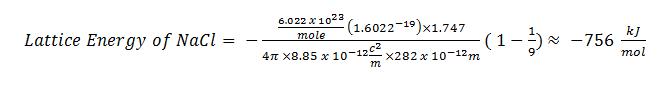The Born-Landé equation is a concept originally formulated in 1918 by the scientists Born and Landé and is used to calculate the lattice energy (measure of the strength of bonds) of a compound. This expression takes into account both the Born interactions as well as the Coulomb attractions.
Introduction
Due to its high simplicity and ease, the Born-Landé equation is commonly used by chemists when solving for lattice energy. This equation proposed by Max Born and Alfred Landé states that lattice energy can be derived from ionic lattice based on electrostatic potential and the potential energy due to repulsion. To solve for the Born-Landé equation, you must have a basic understanding of lattice energy:
- Lattice energy decreases as you go down a group (as atomic radii goes up, lattice energy goes down).
- Going across the periodic table, atomic radii decreases, therefore lattice energy increases.
The Born-Landé equation was derived from these two following equations. the first is the electrostatic potential energy:
\[ \Delta U = - \dfrac{N_A M\left | Z^+ \right | \left | Z^- \right |e^2}{4\pi\epsilon_o r} \label{1} \]
with
- \(M_A\) is Avogadro's constant (\(6.022 \times 10^{23}\))
- \(M\) is the Madelung Constant (a constant that varies for different structures)
- \(e\) is the charge of an electron (\(1.6022 \times 10^{-19}\) C)
- \(Z^+\) is the cation charge
- \(Z^-\) is the anion charge
- \(\epsilon_o\) is the permittivity of free space
The second equation is the repulsive interaction:
\[ \Delta U = \dfrac{N_A B}{r^n} \label{2} \]
with
- \(B\) is the repulsion coefficient and
- \(n\) is the Born Exponent (typically ranges between 5-12) that is used to measure how much a solid compresses
These equations combine to form:
\[ \Delta U (0K) = \dfrac{N_A M\left | Z^+ \right | \left | Z^- \right |e^2}{4\pi\epsilon_or_o} \left ( 1- \dfrac{1}{n} \right) \label{3} \]
with
- \(r_0\) is the closest ion distance
Calculate Lattice Energy
Lattice energy, based on the equation from above, is dependent on multiple factors. We see that the charge of ions is proportional to the increase in lattice energy. In addition, as ions come into closer contact, lattice energy also increases.
Example \(\PageIndex{1}\)
Which compound has the greatest lattice energy?
Solution
This question requires basic knowledge of lattice energy. Since F3 gives the compound a +3 positive charge and the Al gives the compound a -1 negative charge, the compound has large electrostatic attraction. The bigger the electrostatic attraction, the greater the lattice energy.
Example \(\PageIndex{2}\)
What is the lattice energy of NaCl? (Hint: you must look up the values for the constants for this compound)
Solution
-756 kJ/mol (again, this value is found in a table of constants)
Example \(\PageIndex{3}\)
Calculate the lattice energy of NaCl.
Solution