The most important non-octahedral geometries for transition metal complexes are:
4-coordinate: square planar and tetrahedral
5-coordinate: square pyramidal and trigonal bipyramidal
|
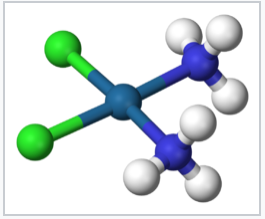
cis-Pt(NH3)2Cl2, a 5d8 square planar complex
|
|
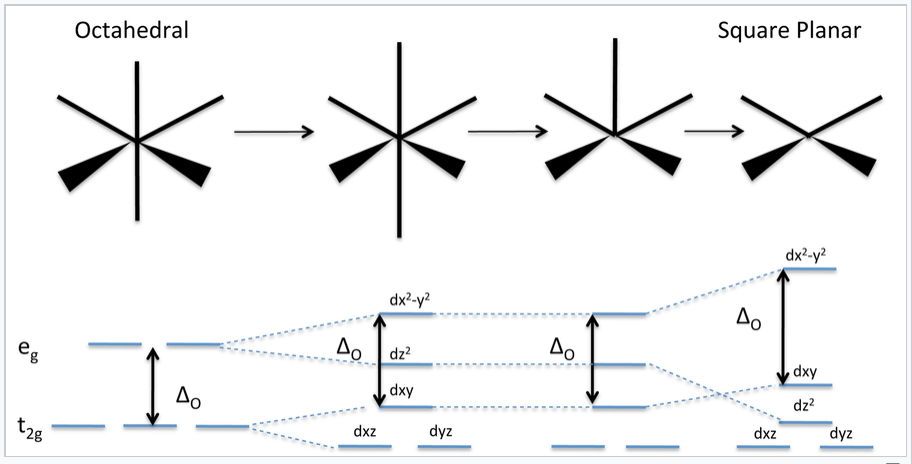
Crystal field energy diagram showing the transition from octahedral to square planar geometry
|
Energies of the d-orbitals in non-octahedral geometries
The figure above shows what happens to the d-orbital energy diagram as we progressively distort an octahedral complex by elongating it along the z-axis (a tetragonal distortion), by removing one of its ligands to make a square pyramid, or by removing both of the ligands along the z-axis to make a square planar complex. In all cases, we keep the total bond order the same by making the bonds in the xy plane shorter as the bonds in the z-direction are stretched and/or broken.
|

Barnett Rosenberg (Michigan State University) accidentally discovered the biological effects of square planar cis-Pt(NH3)2Cl2 while researching bacterial growth in electric fields.[8] The Pt electrode he used reacted with chloride and ammonium ions in the electrolyte to produce the compound at 1-10 ppm concentration. Further experiments revealed that the cis-isomer (but not the trans-isomer) is a potent anti-cancer drug which is especially effective against testicular cancer. The drug works by cross-linking guanine-cytosine rich regions of DNA, thus inhibiting cell division.
|
The distortion away from octahedral symmetry breaks the degeneracy of the t2g and eg orbitals. d-orbitals with a z-component (dxz, dyz, dz2) go down in energy as orbitals that reside in the xy plane (dxy, dx2-y2) rise in energy. The barycenter (the weighted average orbital energy) remains constant. Also, it is important to note that the splitting between the dxy and dx2-y2 orbitals stays constant at ΔO regardless of the nature of the distortion.
Why would a "happy" octahedral complex want to lose two of its ligands to make a square planar complex? This occurs frequently in d8 and sometimes in d9 complexes with large ΔO, i.e., 3d8 complexes with strong field ligands and 4d8, 5d8 complexes with any ligands. Examples of such d8 complexes are [Ni(CN)4]2-, the anti-cancer drug cisplatin (cis-Pt(NH3)2Cl2), [Pd(H2O)4]2+, and [AuCl4]-. At the d8 electron count, the lowest four orbitals are filled and the highest orbital (the dx2-y2) is empty, resulting in a large CFSE. These complexes are diamagnetic and tend to be quite stable. With weak field ligands, 3d8 complexes are octahedral and paramagnetic (e.g., [Ni(H2O)6]2+, which has two unpaired electrons in the eg orbitals.
Square planar complexes in catalysis:
Square planar d8 complexes can be oxidized by two electrons to become octahedral (low spin) d6 complexes, which also have a large CFSE. Because the loss of two electrons is accompanied by the gain of two ligands, this process is called oxidative addition. The reverse process is called reductive elimination. Both processes function together in catalytic cycles, such as the hydrogenation of olefins using Wilkinson's catalyst.[10][11] The catalytic cycle is shown below.
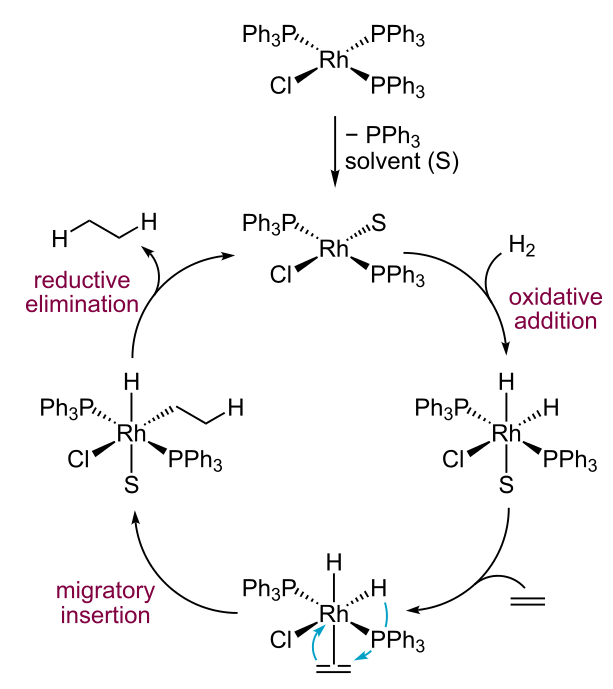
The catalyst cycles between 4-coordinate Rh(I) (4d8) and 6-coordinate Rh(III) (4d6). The complex first adds H2 oxidatively, to give a six-coordinate complex in which the hydrogen is formally H-. An olefin molecule displaces a solvent molecule, using its π-electrons to coordinate the metal. The complex rearranges by inserting the olefin into the metal-hydrogen bond, a process called migratory insertion. Finally, the complex returns to the square planar geometry by eliminating the hydrogenated olefin (reductive elimination). Wilkinson's catalyst is highly active and is widely used for homogeneous hydrogenation, hydroboration, and hydrosilation reactions.[12][13] With chiral phosphine ligands, the catalyst can hydrogenate prochiral olefins to give enantiomerically pure products.[14]
|

Sir Geoffrey Wilkinson, an inorganic chemist at Imperial College London, developed Wilkinson's catalyst in 1966. Earlier, as an Assistant Professor at Harvard University, he had elucidated the sandwich structure of ferrocene,[9] which had been discovered a few years before but not understood. Wilkinson was awarded the Nobel Prize in Chemistry in 1973 for his contributions to organometallic chemistry.
|






