Ligands that contain more than one binding site for a metal ion are called chelating ligands (from the Greek word χηλή, chēlē, meaning "claw"). As the name implies, chelating ligands have high affinity for metal ions relative to ligands with only one binding group (which are called monodentate = "single tooth") ligands.
|
Ethylenediamine (en) is a bidentate ligand that forms a five-membered ring in coordinating to a metal ion M
|
Consider the two complexation equilibria in aqueous solution, between the cobalt (II) ion, Co2+(aq) and ethylenediamine (en) on the one hand and ammonia, NH3, on the other.
\(\ce{[Co(H2O)6]^{2+} + 6NH3 \rightleftharpoons [Co(NH3)6]^{2+} + 6H2O}\) (1)
\(\ce{[Co(H2O)6]^{2+} + 3en \rightleftharpoons [Co(en)3]^{2+} + 6H2O}\) (2)
Electronically, the ammonia and en ligands are very similar, since both bind through N and since the Lewis base strengths of their nitrogen atoms are similar. This means that ΔH° must be very similar for the two reactions, since six Co-N bonds are formed in each case. Interestingly however, we observe that the equilibrium constant is 100,000 times larger for the second reaction than it is for the first.
The big difference between these two reactions is that the second one involves "condensation" of fewer particles to make the complex. This means that the entropy changes for the two reactions are different. The first reaction has a ΔS° value close to zero, because there are the same number of molecules on both sides of the equation. The second one has a positive ΔS° because four molecules come together but seven molecules are produced. The difference between them (ΔΔS°) is about +100 J/mol-K. We can translate this into a ratio of equilibrium constants using:
Kf(en)/Kf(NH3) = e-ΔΔG°/RT ≈ e+ΔΔS°/R ≈ e12 ≈ 105
\[\frac{K_{f}(en)}{K_{f}(NH_{3})} = e^{\frac{-\Delta\Delta G^{o}}{RT}} \approx e^{\frac{+\Delta \Delta S^{o}}{R}} \approx e^{12} \approx 10^{5}\]
The bottom line is that the chelate effect is entropy-driven. It follows that the more binding groups a ligand contains, the more positive the ΔS° and the higher the Kf will be for complex formation. In this regard, the hexadentate ligand ethylenediamine tetraacetic acid (EDTA) is an optimal ligand for making octahedral complexes because it has six binding groups. In basic solutions where all four of the COOH groups are deprotonated, the chelate effect of the EDTA4- ligand is approximately 1015. This means, for a given metal ion, Kf is 1015 times larger for EDTA4- than it would be for the relevant monodentate ligands at the same concentration. EDTA4-tightly binds essentially any 2+, 3+, or 4+ ion in the periodic table, and is a very useful ligand for both analytical applications and separations.
|
Ethylenediaminetetraaceticacid acid (EDTA), a hexadentate ligand
|
The macrocyclic effect follows the same principle as the chelate effect, but the effect is further enhanced by the cyclic conformation of the ligand. Macrocyclic ligands are not only multi-dentate, but because they are covalently constrained to their cyclic form, they allow less conformational freedom. The ligand is said to be "pre-organized" for binding, and there is little entropy penalty for wrapping it around the metal ion. For example heme b is a tetradentate cyclic ligand which is strongly complexes transition metal ions, including (in biological systems) Fe+2.
|
Heme b
|
Some other common chelating and cyclic ligands are shown below:
Acetylacetonate (acac-, right) is an anionic bidentate ligand that coordinates metal ions through two oxygen atoms. Acac- is a hard base so it prefers hard acid cations. With divalent metal ions, acac- forms neutral, volatile complexes such as Cu(acac)2 and Mo(acac)2 that are useful for chemical vapor deposition (CVD) of metal thin films.
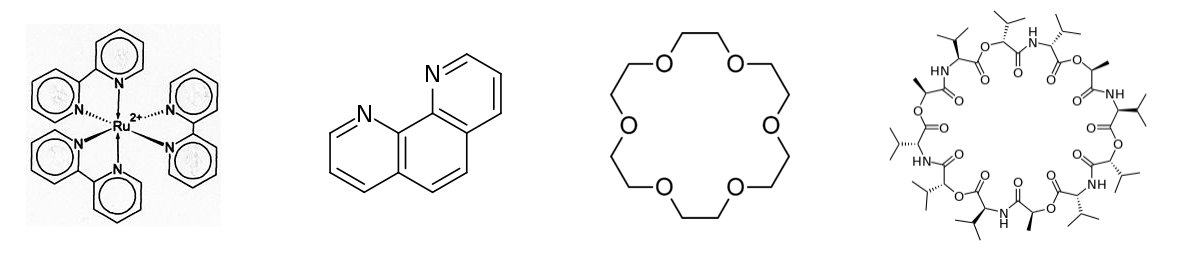
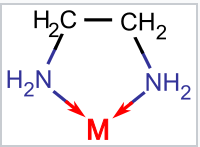
2,2'-Bipyridine and related bidentate ligands such as 1,10-phenanthroline (below, center left) form propeller-shaped complexes with metals such as Ru2+. The [Ru(bpy)3]2+ complex (below left) is photoluminescent and can also undergo photoredox reactions, making it an interesting compound for both photocatalysis and artificial photosynthesis. The chiral propellor shapes of metal polypyridyl complexes such as [Ru(bpy)3]2+ coincidentally match the size and helicity of the major groove of DNA. This has led to a number of interesting studies of electron transfer reactions along the DNA backbone, initiated by photoexcitation of the metal complex.
|

Prof. Jacqueline Barton (Caltech) has used metal polypyridyl complexes to study electron transfer reactions that are implicated in the biological sensing and repair of damage in DNA molecules.
|
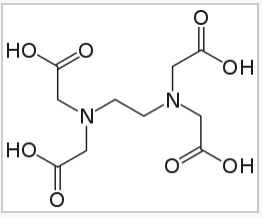
Crown ethers such as 18-crown-6 (below, center right) are cyclic hard bases that can complex alkali metal cations. Crowns can selectively bind Li+, Na+, or K+ depending on the number of ethylene oxide units in the ring.
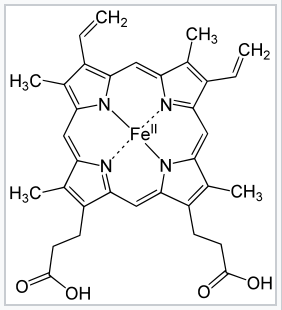
The chelating properties of crown ethers are mimetic of the natural antibiotic valinomycin (below right), which selectively transports K+ ions across bacterial cell membranes, killing the bacterium by dissipating its membrane potential. Like crown ethers, valinomycin is a cyclic hard base.