2.1: Valence Bond Theory- Lewis Dot Structures, the Octet Rule, Formal Charge, Resonance, and the Isoelectronic Principle
- Last updated
- Save as PDF
- Page ID
- 226582
Atoms and Molecules
Atomism, because it was dismissed by Aristotle, enjoyed a long sleep in scientific discourse until it was reconsidered by Galileo, Decartes, and Gassendi in the 1600s. Dalton postulated the modern atomic theory in 1808 based on his observation that elements such as hydrogen and oxygen combined in specific ratios (the Law of Definite Proportions), but the atomic theory remained contentious throughout most of the 19th century. Thompson, Rutherford, Bohr, and others around the turn of the 20th century established that matter was indeed composed of atoms that contained heavy nuclei and light electrons, and that atoms could exist in excited states that could be interpreted as excitations of their electrons to different energy levels. However the atomic theory did not provide a ready explanation for the bonded states of atoms in molecules.
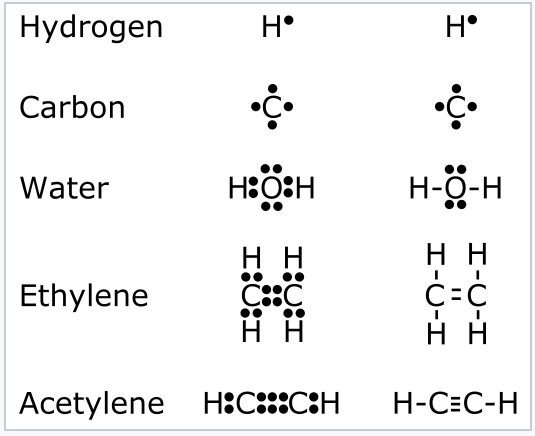
In 1916, still more than a decade before modern quantum theory would adequately describe the shapes of atomic orbitals, Lewis proposed the octet theory based on the empirically observed rules of valence, i.e., the combining ratios of atoms in molecules.[1] This theory, in hindsight, can be rationalized for s- and p-block elements by observing that main-group atoms can use their four valence orbitals (s, px, py, and pz) to accommodate up to eight electrons, some or all of which may be shared with other atoms. In Lewis' model, the valence electrons of an atom were situated at the corners of a cube, and the cubes could share edges or faces to complete their octets. Lewis developed a shorthand notation for these structures based on dots that represented the valence electrons, as illustrated in Fig. \(\PageIndex{1}\). A pair of electrons shared between atoms constitutes a chemical bond, and can also be represented as a line joining the atoms. Four electrons shared between atoms, represented by two lines, is a double bond, and so forth. Any pairs of electrons not involved in bonding form "lone pairs" that belong to one atom only and are thus not involved in bonding.
The Lewis picture is powerful in its simplicity. It can be readily used to rationalize or predict the combining ratios of atoms, to sort plausible and unlikely structures for molecules (including large ones), and to rationalize the acid-base properties of many molecules. It is important to remember that the model is built on a shaky, pre-quantum mechanical description of atoms and so with it, we will make mistakes. Nevertheless it is useful to see how far we can go with the Lewis model.
Constructing the octet valence bond picture for a molecule
We can construct an octet picture for any molecule using the N-V method:
- Number of electrons needed to make separate octets around all atoms = N
- (N = 8 for non-H atoms, N = 2 for H)
- Number of valence electrons = V (add up using group numbers; don't forget to add or subtract for charges on ions)
- Number of shared electrons = S = N-V; and therefore the number of bonds = S/2
- Fill in lone pairs everywhere else to complete octets
Example: nitrate anion, NO3-
- N = 4 atoms x 8 electrons = 32
- V = 5 + 6 + 6 + 6 + 1 = 24 (N + O + O + O + charge)
- S = 32-24 = 8 shared electrons = 4 bonds
- The number of lone pairs is obtained by difference: (V-S)/2 = (24-8)/2 = 8
- Now draw the molecule, starting with the four bonds and adding eight lone pairs to complete the octets:
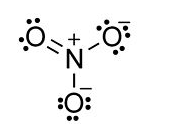
- Count the shared and unshared electrons around each atom in the nitrate ion and you will see that all atoms are octet and that the total number of valence electrons (V) is 24. If you do the N-V calculation according to the rules above, you should always get an octet structure.
|
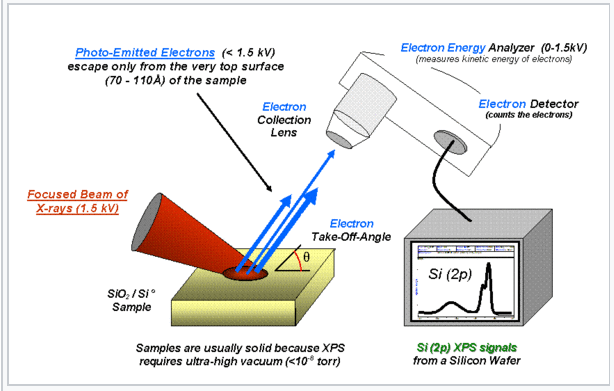
The charges on atoms in a molecule (or an extended solid such as SiO2) can be estimated from X-ray photoelectron spectra (XPS). Energetic X-rays ionize atoms by kicking out electrons from their core orbitals. By conservation of energy, the kinetic energy (KE) of an emitted electron is related to its binding energy (BE) and the energy of the incoming X-ray photon (hν) by BE = hν - KE. Electrons are harder to remove from positively charged atoms (higher BE), and easier to remove from negatively charged atoms (lower BE), relative to the neutral element. |
The formal charge distribution is assigned by dividing the shared (bonding) electrons equally between atoms. Thus, the singly bonded O atoms each possess 7 electrons, and because O is in group 6, their formal charge is -1. The doubly bonded O has a formal charge of zero. The N atom has a formal charge of +1 because it "owns" 4 valence electrons and is in group 5.
Note that the formal charge is not the same thing as the oxidation number (or oxidation state). In the nitrate ion, the oxidation state of nitrogen is +5 and the oxidation state of oxygen is -2. The formal charge is typically closer to the "real" charge on the atom (as measured, e.g., by X-ray photoelectron spectroscopy). Oxidation states are a useful bookkeeping device for keeping track of oxidation-reduction reactions, as we will discuss in Chapter 4. Like oxidation states, the formal charges on the atoms in a molecule or ion must add up to its overall charge.
We can similarly draw the Lewis structure for ammonia as shown below:
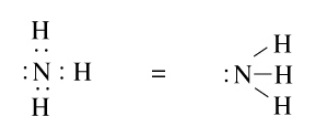
When we divide the shared electrons equally between the atoms, we see that the N atom has five electrons and each H atom has one. These are the same as their group numbers, and thus, all the formal charges in the ammonia molecule are zero.
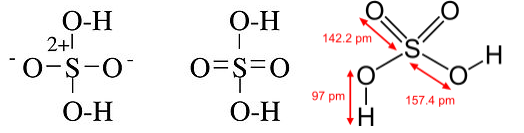
Octet structures of the Lewis acid-base adduct NH3BF3, the hydronium ion H3O+, and the sulfate anion SO42- are shown below. In this case (and in many Lewis structures we will draw), we leave off the implied lone pairs around the peripheral atoms. Try calculating the number of bonds in each of these molecules using the N-V method, and fill in the lone pairs that are not explicitly drawn in.
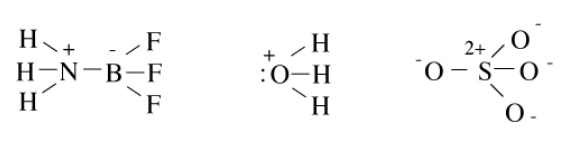
In cases where more than one valence bond structure is possible, we can use formal charges to decide which structures should be more or less stable. The rules are:
- The formal charges on atoms are minimized in stable structures, zero being the best case.
- Negative formal charges should be placed on the most electronegative atom(s).
- Positive formal charges should be placed on the least electronegative atom(s).
- It is unfavorable to place like charges (++ or --) on neighboring atoms in a molecule.
Examples of these rules are shown below for alternative structures of BF3 and ONF.
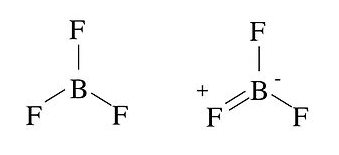
In the BF3 case, the structure on the left is non-octet, because there are only six electrons (three bonds) in the valence shell of B. Such structures are said to be electron deficient. An octet structure (right) can be drawn, but it places a positive formal charge on F, the most electronegative atom in the molecule. Thus, neither structure is completely "happy," but the formal charge rules tell us that the electron-deficient structure on the left is more stable. The electron deficiency of BF3makes it a powerful Lewis acid.
In the case of ONF, the structure on the left is unfavorable for two reasons. First, it places a positive formal charge on F, the most electronegative atom. Second, there is another possible structure (right) that has zero formal charge, which is preferable to one with non-zero charge. This means that the structure on the right, with a double bond between N and O, is more reasonable.

|
Life outside of the ocean owes its existence to the presence of ozone (O3) in the stratosphere. Ozone absorbs the ultraviolet light in the solar spectrum, which otherwise would cause catastrophic damage to DNA and other biological molecules. Because ozone is produced photochemically from O2, which is itself generated by photosynthesis, the spectroscopic signature of ozone in the atmosphere of distant planets is one possible way to look for extraterrestrial life. |
Resonance structures
The ozone (O3) molecule has two equivalent octet structures, shown below:
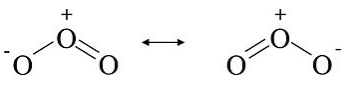
In both cases, the Lewis dot diagram suggests that there are three kinds of oxygen atoms in the molecule, with +1, 0, and -1 formal charges. These structures also suggest that ozone should have one single and one double bond. Experimentally (by electron diffraction), however, we find that the molecule is symmetric, with both O-O bond lengths the same. The real (instantaneous) structure is the average of the two forms, as shown below. In the classical Lewis picture of the molecule, we can rationalize resonance by observing that electrons, being thousands of times lighter than the nuclei of atoms, move very fast on the timescale of molecular vibrations. Thus, in the time it takes for the oxygen atoms to adjust their positions, the electrons can move back and forth many times. In the quantum mechanical MO picture (Chapter 2), we will see that resonance involves electrons that are fully delocalized over the atoms in the molecule. We represent resonance structures with a double-headed arrow to signify that the only difference between the Lewis structures is the distribution of electrons.
|
Susan Solomon discovered the heterogeneous catalytic mechanism whereby ozone is decomposed by chlorofluorocarbons (freons), creating the Antarctic ozone hole. Her work formed the basis of the U.N. Montreal Protocol, an international agreement to protect the ozone layer by regulating damaging chemicals. |
In the instantaneous structure of ozone, the formal (-) charge is shared between the two terminal oxygen atoms and therefore each one has a formal charge of -1/2. The O-O bonds are the average of a single and a double bond, i.e., each O-O bond order is 1.5.
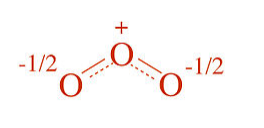
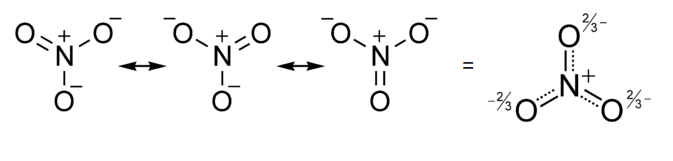
Similarly, the nitrate anion has three resonance structures, and experimentally (by X-ray crystallography of nitrate salts) we find that all the N-O bonds in the ion are the same. In this case, in the averaged structure, each O atom has a formal charge of -2/3 and the N-O bond order is 4/3 (=1.33...).
Inequivalent resonance structures
The rules of resonance also apply to inequivalent structures, which in general will have different energies from each other. In this case the structure of the molecule represents a weighted average of the low energy structures. A good example is the cyanate ion, OCN-. We can write three inequivalent octet structures for the molecule:
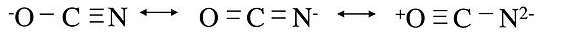
The first two are reasonable resonance structures, although we suspect the one on the left is the best because it puts the negative formal charge on the most electronegative atom. The last one is clearly a bad resonance structure, because the formal charges are high and there is a positive charge on the oxygen atom. The real structure is thus a weighted average of the first two.
No-bond resonance
An interesting and useful kind of inequivalent resonance structure is one in which there is a bond order of zero between two of the atoms. This concept of no-bond resonance is important in understanding the bonding in many halogen- and hydrogen-containing compounds. The idea is illustrated below for the generic molecule X-Y-Z, where Z might be an electronegative halogen atom such as F. By moving the bonding electrons from the Y-Z bond onto the Z atom, and moving a lone pair from X into the X-Y bond, we generate the resonance structure shown on the right in which all atoms remain octet, but there is no bond between Y and Z.

It is important to recognize in this example that the no-bond form is only one resonance structure, and therefore the Z atom is still bound to Y. If the two resonance structures in this example have the same energy, we would expect the X-Y bond order to be 1.5 and the Y-Z bond order to be 0.5. Therefore the Y-Z bond should be longer than it is in a compound where the bond order is one, and it should be relatively easy to break the Y-Z bond.
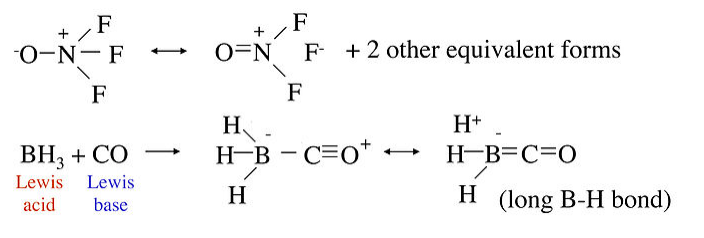
Some molecular examples of no-bond resonance are shown below. In the molecule ONF3, the N-F bond is unusually long relative to the N-F bond in NF3, in which the bond order is 1. This can be explained by the no-bond resonance forms shown on the right. Similarly, in the Lewis acid-base adduct formed by combining BH3 with CO, we can explain the long B-H bonds using no-bond resonance forms that place a partial positive charge on the H atoms.
No-bond resonance is often used to provide an octet bonding picture for so-called hypervalent compounds, which are compounds that appear to have more than 8 valence electrons in the bonding shell of the central atom. For example, we can consider two different valence bond structures for the triiodide ion, I3-, which is formed by reaction of I- with I2 in water:
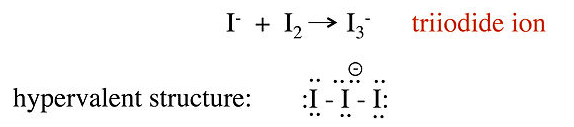
In this structure, the central iodine atom has 10 electrons in its valence shell, in violation of the octet rule. Raman spectra of the triiodide ion show that the I-I bond is weaker than the I-I single bond in I2, suggesting that this picture is not an accurate description of the bonding. A better representation of I3- can be obtained with no-bond resonance structures, as shown below. We will see that this picture is consistent with the MO description of I3- in Chapter 2:
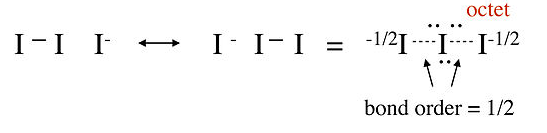
|
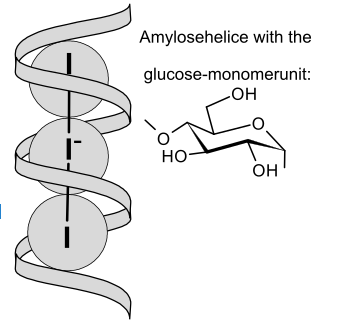
The deep blue color of starch-iodine solutions results from the complexation of linear polyiodide ions (In-) by the starch (amylose) left-handed helix. The interior of the helix is hydrophobic. In electron donor solvents such as ethanol and water, I2 and salts of I3- have a brown color, the result of a charge transfer interaction between the solvent and solute.[2][3]
|
We can draw a similar picture for the XeF2 molecule, which has the same number of valence electrons as I3-. This picture is consistent with XPS data, which show a partial negative charge on the F atoms, as well as vibrational spectra, which show that the Xe-F bond is weaker in XeF2 than it is in the singly-bonded cation Xe-F+.
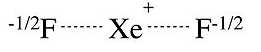
Other well known examples of hypervalent compounds are PF5, P(CH3)5, and SF6, as well as oxyacids such as H2SO4 and HClO4. The hypervalent structure is often drawn for these molecules, with the explanation that d-orbitals on the central atom contribute to the bonding in dsp3 and d2sp3 hybrids for 5- and 6-coordinate molecules, respectively. However, realistic molecular orbital calculations show that the phosphorus and sulfur 3d orbitals are too high in energy to contribute significantly to bonding in PF5 and SF6. For these molecules, we can use no-bond resonance to make reasonable octet structures that predict polar bonds between the central atom and F.
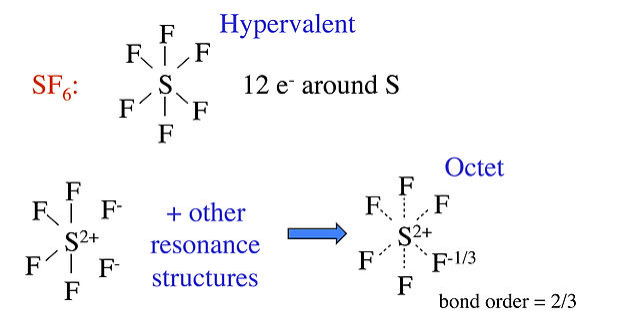
|
Space-filling model of sulfur hexafluoride. SF6 is surprisingly unreactive with water, relative to other compounds that contain S-F bonds. The tight packing of F atoms around S prevents nucleophilic attack by water. |
In other cases, such as P(CH3)5, the octet structure is unreasonable because it suggests a polar bond between P and C, with a partial negative charge on C. Further, in the case of oxyacids such as H2SO4 and HClO4, X-ray crystallographic data establish that the S-O and Cl-O bonds are shorter for the oxygen atoms not bonded to hydrogen, which is more consistent with the hypervalent picture:
The question of whether hypervalency and the octet rule are really useful descriptions of the bonding in these compounds has been considered in a number of computational studies, which have used increasingly accurate quantum mechanical calculations to determine the number of electrons associated with the central atom. In a 2002 study, Gillespie and Silvi[4] found that the population of the valence shell is greater than eight for compounds with electropositive ligands, such as P(CH3)5, and less than eight for compounds such as PF5. They concluded that these valence electron shell populations depend primarily on the coordination numbers and electronegativities of the central atoms and their ligands, and that there is no fundamental difference between the bonding in hypervalent and non-hypervalent (Lewis octet) molecules. This reminds us that the octet rule is not a law of nature, but rather an empirical rule that is useful within certain limits.
The isoelectronic principle
In calculating the octet structures of molecules using the N-V method, we needed to know only the number of atoms and the number of electrons, not the identities of the atoms themselves. This means that we will get the same answer (and the same set of octet and resonance structures) for any molecule or ion that contains (a) the same number of non-hydrogen atoms, and (b) the same total number of valence electrons. Such molecules are said to be isoelectronic. This is a powerful conclusion because, once we have determined the electronic structure of one molecule, we can write down the same solution for all other molecules that are isoelectronic. For example, we noted above that I3- and XeF2, which both have 22 valence electrons, have the same valence bond structure. We can further expect that isoelectronic molecules will have the same shapes and, very often, similar physical properties.
The four molecules and ions below all contain three non-hydrogen atoms and 16 valence electrons. All of them are linear molecules with two double bonds. The four molecules and ions shown below them all contain four non-hydrogen atoms and 24 valence electrons. These four have a trigonal planar shape. While BF3 is a member of this isoelectronic series, we do not write it in the resonance form that contains a B=F double bond, because that would put a positive formal charge on F.
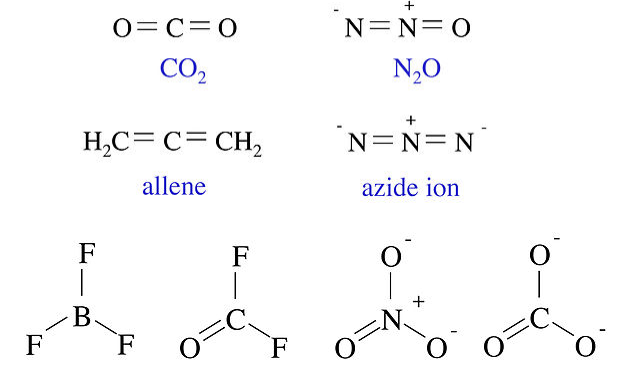
Similarly we can show that CH4, NH3, NH4+, H2O, H3O+, HF, F-, and OH- are all isoelectronic with one non-H atom and eight valence electrons. In the next section we will see that this gives rise to nearly identical electronic shapes for these molecules.
|
Nitrous oxide (N2O), or laughing gas, is isoelectronic with CO2. The two molecules have the same shape (linear) and similar physical properties. CO2 sublimes at -78 °C, whereas N2O melts at -91 °C and boils at -88 °C. |
Isoelectronic solids
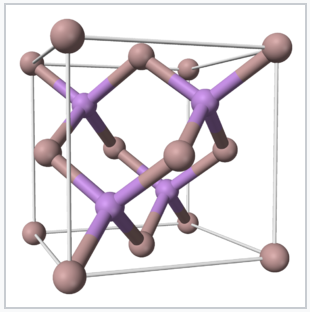
The isoelectronic principle works not just for molecules but for extended solids as well. One technologically important set of isoelectronic solids are the p-block semiconductors. The group 14 element Si is the most widely used semiconductor for electronics, but, as we will discuss later, it is not a good light emitter. Light-emitting diodes (LEDs), which are used in lasers, high efficiency lighting, and display technologies, are made from compounds that are isoelectronic with Si and Ge, especially GaAs, GaP, AlAs, and GaN (all contain four valence electrons per atom). CdTe and CuIn1-xGaxSe2 (CIGS) are promising solar cell materials that also have the same number of valence electrons per atom. Like Si and Ge, these compounds have tetrahedrally bonded structures in the solid state and absorb light across most of the solar spectrum, as we will discuss in more detail in Chapters 8 and 10.
The isoelectronic principle is also a powerful tool in materials research, because it provides guidance about where to look for new materials with similar and perhaps improved properties. For example, the discovery that 8.5% efficient thin layer solar cells could be made with the compound CsSnI3[5] stimulated the exploration of many isoelectronic ABX3 compounds with the same perovskite crystal structure. Very recently thin film solar cells based on light absorbers in this structural family (MA)PbI3-xClx and FAxMA1−xPbBryI3−y (MA+ = methylammonium, CH3NH3+; FA+ = formamidinium, HC(NH2)2+) have been reported with efficiencies as high as 22%.[6][7][8]