8.4: Making Molecules- Mass-to-Mass Conversions
- Page ID
- 48622
- Convert from mass or moles of one substance to mass or moles of another substance in a chemical reaction.
Mole to Mass Conversions
We have established that a balanced chemical equation is balanced in terms of moles, as well as atoms or molecules. We have used balanced equations to set up ratios, in terms of moles of materials, that we can use as conversion factors to answer stoichiometric questions—such as how many moles of substance A react with so many moles of reactant B. We can extend this technique even further. Recall that we can relate a molar amount to a mass amount using molar mass. We can use that relation to answer stoichiometry questions in terms of the masses of a particular substance, in addition to moles. We do this using the following sequence:
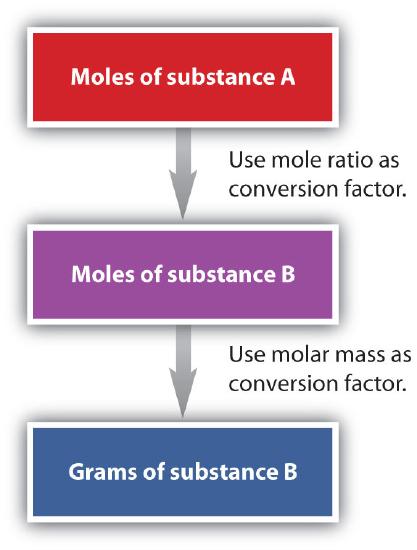
As an example, consider the balanced chemical equation
\[\ce{Fe_2O_3 + 3SO_3 \rightarrow Fe_2(SO_4)_3} \label{Eq1} \]
If we have 3.59 mol of \(\ce{Fe2O3}\), how many grams of \(\ce{SO3}\) can react with it? Using the mole-mass calculation sequence, we can determine the required mass of \(\ce{SO3}\) in two steps. First, we construct the appropriate molar ratio, determined from the balanced chemical equation, to calculate the number of moles of \(\ce{SO3}\) needed. Then, using the molar mass of \(\ce{SO3}\) as a conversion factor, we determine the mass that this number of moles of \(\ce{SO3}\) has.
As usual, we start with the quantity we were given:
\[\mathrm{3.59\: \cancel{ mol\: Fe_2O_3 } \times \left( \dfrac{3\: mol\: SO_3}{1\: \cancel{ mol\: Fe_2O_3}} \right) =10.77\: mol\: SO_3} \label{Eq2} \]
The mol \(\ce{Fe2O3}\) units cancel, leaving mol \(\ce{SO3}\) unit. Now, we take this answer and convert it to grams of \(\ce{SO3}\), using the molar mass of \(\ce{SO3}\) as the conversion factor:
\[\mathrm{10.77\: \bcancel{mol\: SO_3} \times \left( \dfrac{80.06\: g\: SO_3}{1\: \bcancel{ mol\: SO_3}} \right) =862\: g\: SO_3} \label{Eq3} \]
Our final answer is expressed to three significant figures. Thus, in a two-step process, we find that 862 g of \(\ce{SO3}\) will react with 3.59 mol of \(\ce{Fe2O3}\). Many problems of this type can be answered in this manner.
The same two-step problem can also be worked out in a single line, rather than as two separate steps, as follows:
\[ 3.59 \cancel{\, mol \, Fe_2O_3} \times \underbrace{\left( \dfrac{ 3 \bcancel{ \, mol\, SO_3}}{ 1 \cancel{\, mol\, Fe_2O_3}} \right)}_{\text{converts to moles of SO}_3} \times \underbrace{ \left( \dfrac{ 80.06 {\, g \, SO_3}}{ 1 \, \bcancel{ mol\, SO_3}} \right)}_{\text{converts to grams of SO}_3} = 862\, g\, SO_3 \nonumber \]
We get exactly the same answer when combining all math steps together.
How many moles of \(\ce{HCl}\) will be produced when 249 g of \(\ce{AlCl3}\) are reacted according to this chemical equation?
\[\ce{2AlCl_3 + 3H_2O(ℓ) → Al_2O_3 + 6HCl(g)} \nonumber \]
Solution
| Steps for Problem Solving | Example \(\PageIndex{1}\) |
|---|---|
| Identify the "given" information and what the problem is asking you to "find." | Given: 249 g AlCl3 Find: moles HCl |
| List other known quantities. | 1 mol AlCl3 = 133.33 g AlCl3 6 mol of HCl to 2 mol AlCl3 |
| Prepare a concept map and use the proper conversion factor. |
|
| Cancel units and calculate. | \(249\, \cancel{g\, AlCl_{3}}\times \dfrac{1\, \cancel{mol\, AlCl_{3}}}{133.33\, \cancel{g\, AlCl_{3}}}\times \dfrac{6\, mol\, HCl}{2\, \cancel{mol\, AlCl_{3}}}=5.60\, mol\, HCl\) |
| Think about your result. | Since 249 g of AlCl3 is less than 266.66 g, the mass for 2 moles of AlCl3 and the relationship is 6 mol of HCl to 2 mol AlCl3 , the answer should be less than 6 moles of HCl. |
How many moles of \(\ce{Al2O3}\) will be produced when 23.9 g of \(\ce{H2O}\) are reacted according to this chemical equation?
\[\ce{2AlCl_3 + 3H_2O(ℓ) → Al_2O_3 + 6HCl(g)} \nonumber \]
- Answer
- 0.442 mol Al2O3
Mass to Mass Conversions
It is a small step from mole-mass calculations to mass-mass calculations. If we start with a known mass of one substance in a chemical reaction (instead of a known number of moles), we can calculate the corresponding masses of other substances in the reaction. The first step in this case is to convert the known mass into moles, using the substance’s molar mass as the conversion factor. Then—and only then—we use the balanced chemical equation to construct a conversion factor to convert that quantity to moles of another substance, which in turn can be converted to a corresponding mass. Sequentially, the process is as follows:
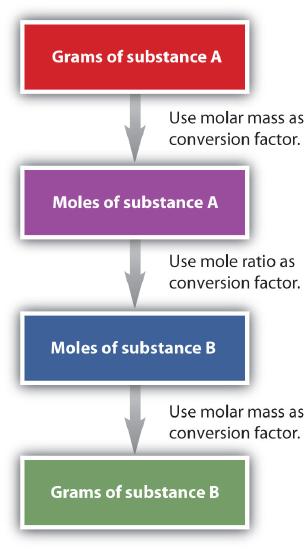
This three-part process can be carried out in three discrete steps or combined into a single calculation that contains three conversion factors. The following example illustrates both techniques. Flowchart of mole mass calculations: To convert from grams to moles of substance A, use molar mass conversion factor; To convert from moles of substance A to moles of substance B, use the mole ratio conversion factor, and to convert from moles to grams of substance B, use molar mass conversion factor
Ammonium nitrate decomposes to dinitrogen monoxide and water according to the following equation.
\[\ce{NH_4NO_3} \left( s \right) \rightarrow \ce{N_2O} \left( g \right) + 2 \ce{H_2O} \left( l \right) \nonumber \]
In a certain experiment, \(45.7 \: \text{g}\) of ammonium nitrate is decomposed. Find the mass of each of the products formed.
| Steps for Problem Solving | Example \(\PageIndex{2}\) |
|---|---|
| Identify the "given" information and what the problem is asking you to "find." |
Given: \(45.7 \: \text{g} \: \ce{NH_4NO_3}\) Mass \(\ce{N_2O} = ? \: \text{g}\) Mass \(\ce{H_2O} = ? \: \text{g}\) |
| List other known quantities. |
1 mol \(\ce{NH_4NO_3} = 80.06 \: \text{g}\) 1 mol \(\ce{N_2O} = 44.02 \: \text{g}\) 1 mol \(\ce{H_2O} = 18.02 \: \text{g}\) 1 mol NH4NO3 to 1 mol N2O to 2 mol H2O |
| Prepare two concept maps and use the proper conversion factor. |
|
| Cancel units and calculate. |
\(45.7 \: \text{g} \: \ce{NH_4NO_3} \times \dfrac{1 \: \text{mol} \: \ce{NH_4NO_3}}{80.06 \: \text{g} \: \ce{NH_4NO_3}} \times \dfrac{1 \: \text{mol} \: \ce{N_2O}}{1 \: \text{mol} \: \ce{NH_4NO_3}} \times \dfrac{44.02 \: \text{g} \: \ce{N_2O}}{1 \: \text{mol} \: \ce{N_2O}} = 25.1 \: \text{g} \: \ce{N_2O}\) \(45.7 \: \text{g} \: \ce{NH_4NO_3} \times \dfrac{1 \: \text{mol} \: \ce{NH_4NO_3}}{80.06 \: \text{g} \: \ce{NH_4NO_3}} \times \dfrac{2 \: \text{mol} \: \ce{H_2O}}{1 \: \text{mol} \: \ce{NH_4NO_3}} \times \dfrac{18.02 \: \text{g} \: \ce{H_2O}}{1 \: \text{mol} \: \ce{H_2O}} = 20.6 \: \text{g} \: \ce{H_2O}\) |
| Think about your result. | The total mass of the two products is equal to the mass of ammonium nitrate which decomposed, demonstrating the law of conservation of mass. Each answer has three significant figures. |
Methane can react with elemental chlorine to make carbon tetrachloride (\(\ce{CCl_4}\)). The balanced chemical equation is as follows:
\[\ce{CH4 (g) + 4 Cl2 (g) → CCl2 (l) + 4 HCl (l) } \nonumber \]
How many grams of \(\ce{HCl}\) are produced by the reaction of 100.0 g of \(\ce{CH4}\)?
- Answer
- 908.7g HCl
Summary
- Calculations involving conversions between moles of a substance and the mass of that substance can be done using conversion factors.
- A balanced chemical reaction can be used to determine molar and mass relationships between substances.

