6.4: The Nature of Light (Exercises)
- Page ID
- 220536
Conceptual Questions
1.1 The Propagation of Light
1. Under what conditions can light be modeled like a ray? Like a wave?
2. Why is the index of refraction always greater than or equal to 1?
3. Does the fact that the light flash from lightning reaches you before its sound prove that the speed of light is extremely large or simply that it is greater than the speed of sound? Discuss how you could use this effect to get an estimate of the speed of light.
4. Speculate as to what physical process might be responsible for light traveling more slowly in a medium than in a vacuum.
1.2 The Law of Reflection
5. Using the law of reflection, explain how powder takes the shine off of a person’s nose. What is the name of the optical effect?
1.3 Refraction
6. Diffusion by reflection from a rough surface is described in this chapter. Light can also be diffused by refraction. Describe how this occurs in a specific situation, such as light interacting with crushed ice.
7. Will light change direction toward or away from the perpendicular when it goes from air to water? Water to glass? Glass to air?
8. Explain why an object in water always appears to be at a depth shallower than it actually is?
9. Explain why a person’s legs appear very short when wading in a pool. Justify your explanation with a ray diagram showing the path of rays from the feet to the eye of an observer who is out of the water.
10. Explain why an oar that is partially submerged in water appears bent.
1.4 Total Internal Reflection
11. A ring with a colorless gemstone is dropped into water. The gemstone becomes invisible when submerged. Can it be a diamond? Explain.
12. The most common type of mirage is an illusion that light from faraway objects is reflected by a pool of water that is not really there. Mirages are generally observed in deserts, when there is a hot layer of air near the ground. Given that the refractive index of air is lower for air at higher temperatures, explain how mirages can be formed.
13. How can you use total internal reflection to estimate the index of refraction of a medium?
1.5 Dispersion
14. Is it possible that total internal reflection plays a role in rainbows? Explain in terms of indices of refraction and angles, perhaps referring to that shown below. Some of us have seen the formation of a double rainbow; is it physically possible to observe a triple rainbow? A photograph of a double rainbow.

15. A high-quality diamond may be quite clear and colorless, transmitting all visible wavelengths with little absorption. Explain how it can sparkle with flashes of brilliant color when illuminated by white light.
1.6 Huygens’s Principle
16. How do wave effects depend on the size of the object with which the wave interacts? For example, why does sound bend around the corner of a building while light does not?
17. Does Huygens’s principle apply to all types of waves?
18. If diffraction is observed for some phenomenon, it is evidence that the phenomenon is a wave. Does the reverse hold true? That is, if diffraction is not observed, does that mean the phenomenon is not a wave?
1.7 Polarization
19. Can a sound wave in air be polarized? Explain.
20. No light passes through two perfect polarizing filters with perpendicular axes. However, if a third polarizing filter is placed between the original two, some light can pass. Why is this? Under what circumstances does most of the light pass?
21. Explain what happens to the energy carried by light that it is dimmed by passing it through two crossed polarizing filters.
22. When particles scattering light are much smaller than its wavelength, the amount of scattering is proportional to \(\displaystyle \frac{1}{λ}\). Does this mean there is more scattering for small \(\displaystyle λ\) than large \(\displaystyle λ\)? How does this relate to the fact that the sky is blue?
23. Using the information given in the preceding question, explain why sunsets are red.
24. When light is reflected at Brewster’s angle from a smooth surface, it is \(\displaystyle 100%\) polarized parallel to the surface. Part of the light will be refracted into the surface. Describe how you would do an experiment to determine the polarization of the refracted light. What direction would you expect the polarization to have and would you expect it to be \(\displaystyle 100%\)?
25. If you lie on a beach looking at the water with your head tipped slightly sideways, your polarized sunglasses do not work very well. Why not?
Problems
1.1 The Propagation of Light
26. What is the speed of light in water? In glycerine?
27. What is the speed of light in air? In crown glass?
28. Calculate the index of refraction for a medium in which the speed of light is \(\displaystyle 2.012×10^8m/s\), and identify the most likely substance based on Table 6.2.1.1.
29. In what substance in Table 6.2.1.1 is the speed of light \(\displaystyle 2.290×10^8m/s\)?
30. There was a major collision of an asteroid with the Moon in medieval times. It was described by monks at Canterbury Cathedral in England as a red glow on and around the Moon. How long after the asteroid hit the Moon, which is \(\displaystyle 3.84×10^5km\) away, would the light first arrive on Earth?
31. Components of some computers communicate with each other through optical fibers having an index of refraction \(\displaystyle n=1.55\). What time in nanoseconds is required for a signal to travel 0.200 m through such a fiber?
32. Compare the time it takes for light to travel 1000 m on the surface of Earth and in outer space.
33. How far does light travel underwater during a time interval of \(\displaystyle 1.50×10^{−6}s\)?
1.2 The Law of Reflection
34. Suppose a man stands in front of a mirror as shown below. His eyes are 1.65 m above the floor and the top of his head is 0.13 m higher. Find the height above the floor of the top and bottom of the smallest mirror in which he can see both the top of his head and his feet. How is this distance related to the man’s height?
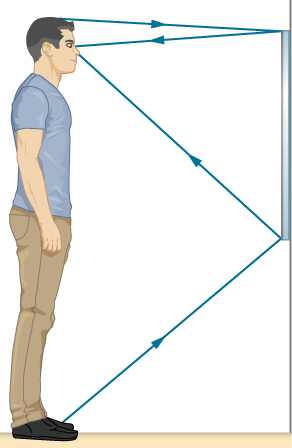
The figure is a drawing of a man standing in front of a mirror and looking at his image. The mirror is about half as tall as the man, with the top of the mirror above his eyes but below the top of his head. The light rays from his feet reach the bottom of the mirror and reflect to his eyes. The rays from the top of his head reach the top of the mirror and reflect to his eyes.
35. Show that when light reflects from two mirrors that meet each other at a right angle, the outgoing ray is parallel to the incoming ray, as illustrated below.
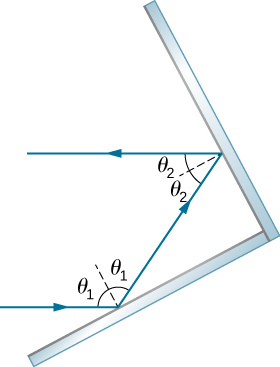
Two mirrors meet each other at a right angle. An incoming ray of light hits one mirror at an angle of theta one to the normal, is reflected at the same angle of theta one on the other side of the normal, then hits the other mirror at an angle of theta two to the normal and reflects at the same angle of theta two on the other side of the normal, such that the outgoing ray is parallel to the incoming ray.
36. On the Moon’s surface, lunar astronauts placed a corner reflector, off which a laser beam is periodically reflected. The distance to the Moon is calculated from the round-trip time. What percent correction is needed to account for the delay in time due to the slowing of light in Earth’s atmosphere? Assume the distance to the Moon is precisely \(\displaystyle 3.84×10^8m\) and Earth’s atmosphere (which varies in density with altitude) is equivalent to a layer 30.0 km thick with a constant index of refraction \(\displaystyle n=1.000293\).
37. A flat mirror is neither converging nor diverging. To prove this, consider two rays originating from the same point and diverging at an angle \(\displaystyle θ\) (see below). Show that after striking a plane mirror, the angle between their directions remains \(\displaystyle θ\).

Light rays diverging from a point at an angle theta are incident on a mirror at two different places and their reflected rays diverge. One ray hits at an angle theta one from the normal, and reflects at the same angle theta one on the other side of the normal. The other ray hits at a larger angle theta two from the normal, and reflects at the same angle theta two on the other side of the normal. When the reflected rays are extended backwards from their points of reflection, they meet at a point behind the mirror, at the same angle theta with which they left the source.
1.3 Refraction
Unless otherwise specified, for problems 1 through 10, the indices of refraction of glass and water should be taken to be 1.50 and 1.333, respectively.
38. A light beam in air has an angle of incidence of \(\displaystyle 35°\) at the surface of a glass plate. What are the angles of reflection and refraction?
39. A light beam in air is incident on the surface of a pond, making an angle of \(\displaystyle 20°\)20° with respect to the surface. What are the angles of reflection and refraction?
40. When a light ray crosses from water into glass, it emerges at an angle of \(\displaystyle 30°\) with respect to the normal of the interface. What is its angle of incidence?
41. A pencil flashlight submerged in water sends a light beam toward the surface at an angle of incidence of \(\displaystyle 30°\). What is the angle of refraction in air?
42. Light rays from the Sun make a \(\displaystyle 30°\) angle to the vertical when seen from below the surface of a body of water. At what angle above the horizon is the Sun?
43. The path of a light beam in air goes from an angle of incidence of \(\displaystyle 35°\) to an angle of refraction of \(\displaystyle 22°\) when it enters a rectangular block of plastic. What is the index of refraction of the plastic?
44. A scuba diver training in a pool looks at his instructor as shown below. What angle does the ray from the instructor’s face make with the perpendicular to the water at the point where the ray enters? The angle between the ray in the water and the perpendicular to the water is \(\displaystyle 25.0°\).
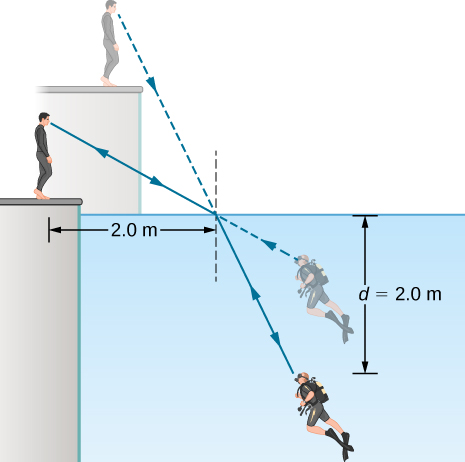
A scuba diver and his trainer look at each other. They see each other at the locations given by straight line extrapolations of the rays reaching their eyes. To the trainer, the scuba diver appears less deep than he actually is, and to the diver, the trainer appears higher than he actually is. To the trainer, the scuba diver's feet appear to be at a depth of two point zero meters. The incident ray from the trainer strikes the water surface at a horizontal distance of two point zero meters from the trainer. The diver’s head is a vertical distance of d equal to two point zero meters below the surface of the water.
45. (a) Using information in the preceding problem, find the height of the instructor’s head above the water, noting that you will first have to calculate the angle of incidence.
(b) Find the apparent depth of the diver’s head below water as seen by the instructor.
1.4 Total Internal Reflection
46. Verify that the critical angle for light going from water to air is \(\displaystyle 48.6°\), as discussed at the end of Example 1.4, regarding the critical angle for light traveling in a polystyrene (a type of plastic) pipe surrounded by air.
47. (a) At the end of Example 1.4, it was stated that the critical angle for light going from diamond to air is \(\displaystyle 24.4°\). Verify this.
(b) What is the critical angle for light going from zircon to air?
48. An optical fiber uses flint glass clad with crown glass. What is the critical angle?
49. At what minimum angle will you get total internal reflection of light traveling in water and reflected from ice?
50. Suppose you are using total internal reflection to make an efficient corner reflector. If there is air outside and the incident angle is \(\displaystyle 45.0°\), what must be the minimum index of refraction of the material from which the reflector is made?
51. You can determine the index of refraction of a substance by determining its critical angle.
(a) What is the index of refraction of a substance that has a critical angle of \(\displaystyle 68.4°\) when submerged in water? What is the substance, based on Table 6.2.1.1?
(b) What would the critical angle be for this substance in air?
52. A ray of light, emitted beneath the surface of an unknown liquid with air above it, undergoes total internal reflection as shown below. What is the index of refraction for the liquid and its likely identification?
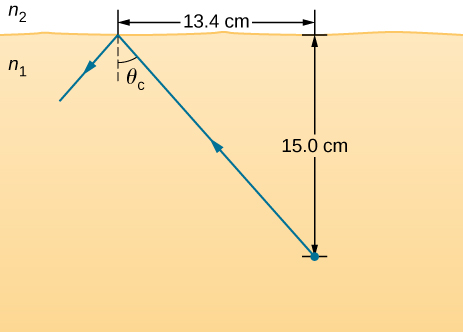
A light ray travels from an object placed in a medium n 1 at 15.0 centimeters below the horizontal interface with medium n 2. This ray gets totally internally reflected with theta c as critical angle. The horizontal distance between the object and the point of incidence is 13.4 centimeters.
53. Light rays fall normally on the vertical surface of the glass prism (\(\displaystyle n=1.50\) shown below.
(a) What is the largest value for \(\displaystyle ϕ\) such that the ray is totally reflected at the slanted face?
(b) Repeat the calculation of part (a) if the prism is immersed in water.
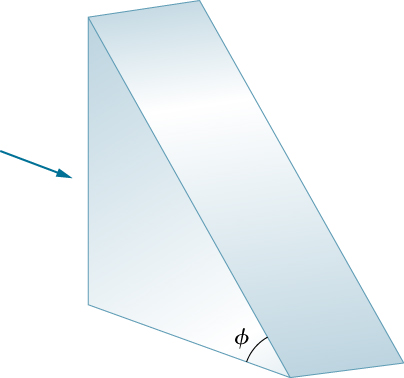
A right angle triangular prism has a horizontal base and a vertical side. The hypotenuse of the triangle makes an angle of phi with the horizontal base. A horizontal light rays is incident normally on the vertical surface of the prism.
1.5 Dispersion
54. (a) What is the ratio of the speed of red light to violet light in diamond, based on Table 6.2.4.1?
(b) What is this ratio in polystyrene?
(c) Which is more dispersive?
55. A beam of white light goes from air into water at an incident angle of \(\displaystyle 75.0°\). At what angles are the red (660 nm) and violet (410 nm) parts of the light refracted?
56. By how much do the critical angles for red (660 nm) and violet (410 nm) light differ in a diamond surrounded by air?
57. (a) A narrow beam of light containing yellow (580 nm) and green (550 nm) wavelengths goes from polystyrene to air, striking the surface at a \(\displaystyle 30.0°\) incident angle. What is the angle between the colors when they emerge?
(b) How far would they have to travel to be separated by 1.00 mm?
58. A parallel beam of light containing orange (610 nm) and violet (410 nm) wavelengths goes from fused quartz to water, striking the surface between them at a \(\displaystyle 60.0°\) incident angle. What is the angle between the two colors in water?
59. A ray of 610-nm light goes from air into fused quartz at an incident angle of \(\displaystyle 55.0°\). At what incident angle must 470 nm light enter flint glass to have the same angle of refraction?
60. A narrow beam of light containing red (660 nm) and blue (470 nm) wavelengths travels from air through a 1.00-cm-thick flat piece of crown glass and back to air again. The beam strikes at a \(\displaystyle 30.0°\) incident angle.
(a) At what angles do the two colors emerge?
(b) By what distance are the red and blue separated when they emerge?
61. A narrow beam of white light enters a prism made of crown glass at a \(\displaystyle 45.0°\) incident angle, as shown below. At what angles, \(\displaystyle θ_R\) and \(\displaystyle θ_V\), do the red (660 nm) and violet (410 nm) components of the light emerge from the prism?
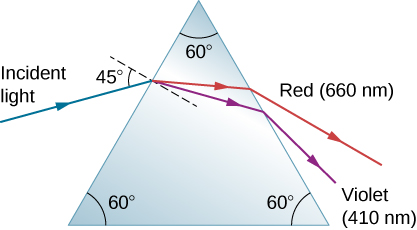
A blue incident light ray at an angle of incidence equal to 45 degrees to the normal falls on an equilateral triangular prism whose corners are all at angles equal to 60 degrees. At the first surface, the ray refracts and splits into red and violet rays. These rays hit the second surface and emerge from the prism. The red light with 660 nanometers bends less than the violet light with 410 nanometers.
1.7 Polarization
62. What angle is needed between the direction of polarized light and the axis of a polarizing filter to cut its intensity in half?
63. The angle between the axes of two polarizing filters is \(\displaystyle 45.0°\). By how much does the second filter reduce the intensity of the light coming through the first?
64. Two polarizing sheets \(\displaystyle P_1\) and \(\displaystyle P_2\) are placed together with their transmission axes oriented at an angle \(\displaystyle θ\) to each other. What is \(\displaystyle θ\) when only \(\displaystyle 25%\) of the maximum transmitted light intensity passes through them?
65. Suppose that in the preceding problem the light incident on \(\displaystyle P_1\) is unpolarized. At the determined value of \(\displaystyle θ\), what fraction of the incident light passes through the combination?
66. If you have completely polarized light of intensity \(\displaystyle 150W/m^2\), what will its intensity be after passing through a polarizing filter with its axis at an \(\displaystyle 89.0°\) angle to the light’s polarization direction?
67. What angle would the axis of a polarizing filter need to make with the direction of polarized light of intensity \(\displaystyle 1.00kW/m^2\) to reduce the intensity to \(\displaystyle 10.0W/m^2\)?
68. At the end of Example 1.7, it was stated that the intensity of polarized light is reduced to \(\displaystyle 90.0%\) of its original value by passing through a polarizing filter with its axis at an angle of \(\displaystyle 18.4°\) to the direction of polarization. Verify this statement.
69. Show that if you have three polarizing filters, with the second at an angle of \(\displaystyle 45.0°\) to the first and the third at an angle of \(\displaystyle 90.0°\) to the first, the intensity of light passed by the first will be reduced to \(\displaystyle 25.0%\) of its value. (This is in contrast to having only the first and third, which reduces the intensity to zero, so that placing the second between them increases the intensity of the transmitted light.)
70. Three polarizing sheets are placed together such that the transmission axis of the second sheet is oriented at \(\displaystyle 25.0°\) to the axis of the first, whereas the transmission axis of the third sheet is oriented at \(\displaystyle 40.0°\) (in the same sense) to the axis of the first. What fraction of the intensity of an incident unpolarized beam is transmitted by the combination?
71. In order to rotate the polarization axis of a beam of linearly polarized light by \(\displaystyle 90.0°\), a student places sheets \(\displaystyle P_1\) and \(\displaystyle P_2\) with their transmission axes at \(\displaystyle 45.0°\) and \(\displaystyle 90.0°\), respectively, to the beam’s axis of polarization.
(a) What fraction of the incident light passes through \(\displaystyle P_1\) and
(b) through the combination?
(c) Repeat your calculations for part (b) for transmission-axis angles of \(\displaystyle 30.0°\) and \(\displaystyle 90.0°\), respectively.
72. It is found that when light traveling in water falls on a plastic block, Brewster’s angle is \(\displaystyle 50.0°\). What is the refractive index of the plastic?
73. At what angle will light reflected from diamond be completely polarized?
74. What is Brewster’s angle for light traveling in water that is reflected from crown glass?
75. A scuba diver sees light reflected from the water’s surface. At what angle will this light be completely polarized?
Additional Problems
76. From his measurements, Roemer estimated that it took 22 min for light to travel a distance equal to the diameter of Earth’s orbit around the Sun.
(a) Use this estimate along with the known diameter of Earth’s orbit to obtain a rough value of the speed of light.
(b) Light actually takes 16.5 min to travel this distance. Use this time to calculate the speed of light.
77. Cornu performed Fizeau’s measurement of the speed of light using a wheel of diameter 4.00 cm that contained 180 teeth. The distance from the wheel to the mirror was 22.9 km. Assuming he measured the speed of light accurately, what was the angular velocity of the wheel?
78. Suppose you have an unknown clear substance immersed in water, and you wish to identify it by finding its index of refraction. You arrange to have a beam of light enter it at an angle of \(\displaystyle 45.0°\), and you observe the angle of refraction to be \(\displaystyle 40.3°\). What is the index of refraction of the substance and its likely identity?
79. Shown below is a ray of light going from air through crown glass into water, such as going into a fish tank. Calculate the amount the ray is displaced by the glass \(\displaystyle (Δx)\), given that the incident angle is \(\displaystyle 40.0°\). and the glass is 1.00 cm thick.
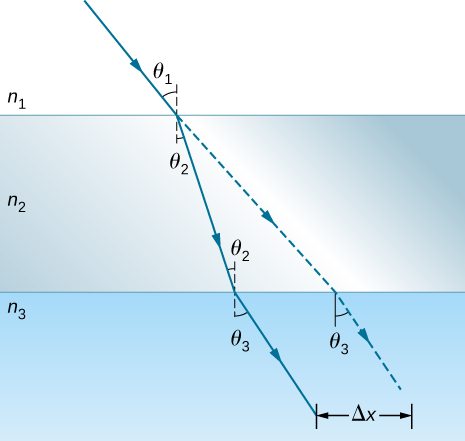
The figure illustrates refraction occurring when light travels from medium \(\displaystyle n_1\) to \(\displaystyle n_3\) through an intermediate medium \(\displaystyle n_2\). The incident ray makes an angle \(\displaystyle θ_1\) with a perpendicular drawn at the point of incidence at the interface between \(\displaystyle n_1\) and \(\displaystyle n_2\). The light ray entering \(\displaystyle n_2\) bends towards the perpendicular line making an angle \(\displaystyle θ_2\) with it on the \(\displaystyle n_2\) side. The ray arrives at the interface between \(\displaystyle n_2\) and \(\displaystyle n_3\) at an angle of \(\displaystyle θ_2\) to a perpendicular drawn at the point of incidence at this interface, and the transmitted ray bends away from the perpendicular, making an angle of theta three to the perpendicular on the \(\displaystyle n_3\) side. A straight line extrapolation of the original incident ray is shown as a dotted line. This line is parallel to the refracted ray in the third medium, \(\displaystyle n_3\), and is shifted a distance delta x from the refracted ray. The extrapolated ray is at the same angle theta three to the perpendicular in medium \(\displaystyle n_3\) as the refracted ray.
80. Considering the previous problem, show that \(\displaystyle θ_3\) is the same as it would be if the second medium were not present.
81. At what angle is light inside crown glass completely polarized when reflected from water, as in a fish tank?
82. Light reflected at \(\displaystyle 55.6°\) from a window is completely polarized. What is the window’s index of refraction and the likely substance of which it is made?
83. (a) Light reflected at \(\displaystyle 62.5°\) from a gemstone in a ring is completely polarized. Can the gem be a diamond?
(b) At what angle would the light be completely polarized if the gem was in water?
84. If \(\displaystyle θ_b\) is Brewster’s angle for light reflected from the top of an interface between two substances, and \(\displaystyle θ'_b\) is Brewster’s angle for light reflected from below, prove that \(\displaystyle θ_b+θ'_b=90.0°\).
85. Unreasonable results Suppose light travels from water to another substance, with an angle of incidence of \(\displaystyle 10.0°\) and an angle of refraction of \(\displaystyle 14.9°\).
(a) What is the index of refraction of the other substance?
(b) What is unreasonable about this result?
(c) Which assumptions are unreasonable or inconsistent?
86. Unreasonable results Light traveling from water to a gemstone strikes the surface at an angle of \(\displaystyle 80.0°\) and has an angle of refraction of \(\displaystyle 15.2°\).
(a) What is the speed of light in the gemstone?
(b) What is unreasonable about this result?
(c) Which assumptions are unreasonable or inconsistent?
87. If a polarizing filter reduces the intensity of polarized light to \(\displaystyle 50.0%\) of its original value, by how much are the electric and magnetic fields reduced?
88. Suppose you put on two pairs of polarizing sunglasses with their axes at an angle of \(\displaystyle 15.0°\). How much longer will it take the light to deposit a given amount of energy in your eye compared with a single pair of sunglasses? Assume the lenses are clear except for their polarizing characteristics.
89. (a) On a day when the intensity of sunlight is \(\displaystyle 1.00kW/m^2\), a circular lens 0.200 m in diameter focuses light onto water in a black beaker. Two polarizing sheets of plastic are placed in front of the lens with their axes at an angle of \(\displaystyle 20.0°\). Assuming the sunlight is unpolarized and the polarizers are \(\displaystyle 100%\) efficient, what is the initial rate of heating of the water in \(\displaystyle °C/s\), assuming it is \(\displaystyle 80.0%\) absorbed? The aluminum beaker has a mass of 30.0 grams and contains 250 grams of water.
(b) Do the polarizing filters get hot? Explain.
Challenge Problems
90. Light shows staged with lasers use moving mirrors to swing beams and create colorful effects. Show that a light ray reflected from a mirror changes direction by \(\displaystyle 2θ\) when the mirror is rotated by an angle \(\displaystyle θ\).
91. Consider sunlight entering Earth’s atmosphere at sunrise and sunset—that is, at a \(\displaystyle 90.0°\). incident angle. Taking the boundary between nearly empty space and the atmosphere to be sudden, calculate the angle of refraction for sunlight. This lengthens the time the Sun appears to be above the horizon, both at sunrise and sunset. Now construct a problem in which you determine the angle of refraction for different models of the atmosphere, such as various layers of varying density. Your instructor may wish to guide you on the level of complexity to consider and on how the index of refraction varies with air density.
92. A light ray entering an optical fiber surrounded by air is first refracted and then reflected as shown below. Show that if the fiber is made from crown glass, any incident ray will be totally internally reflected.
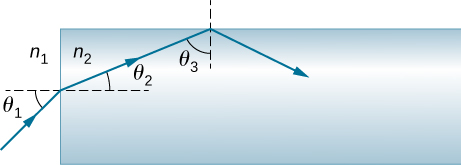
The figure shows light traveling from \(\displaystyle n_1\) and incident onto the left face of a rectangular block of material \(\displaystyle n_2\). The ray is incident at an angle of incidence \(\displaystyle θ_1\), measured relative to the normal to the surface where the ray enters. The angle of refraction is \(\displaystyle θ_2\), again, relative to the normal to the surface. The refracted ray falls onto the upper face of the block and gets totally internally reflected with \(\displaystyle θ_3\) as the angle of incidence.
93. A light ray falls on the left face of a prism (see below) at the angle of incidence \(\displaystyle θ\) for which the emerging beam has an angle of refraction \(\displaystyle θ\) at the right face. Show that the index of refraction n of the glass prism is given by \(\displaystyle n=\frac{sin\frac{1}{2}(α+ϕ)}{sin\frac{1}{2}ϕ}\) where \(\displaystyle ϕ\) is the vertex angle of the prism and \(\displaystyle α\) is the angle through which the beam has been deviated. If \(\displaystyle α=37.0°\) and the base angles of the prism are each \(\displaystyle 50.0°\), what is n?
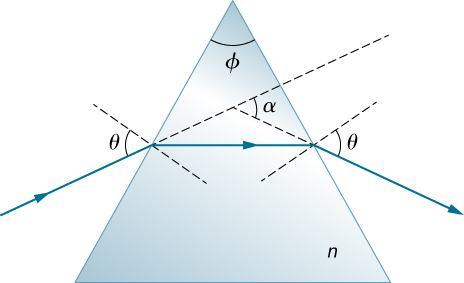
A light ray falls on the left face of a triangular prism whose upper vertex has an angle of phi and whose index of refraction is n. The angle of incidence of the ray relative to the normal to the left face is theta. The ray refracts in the prism. The refracted ray is horizontal, parallel to the base of the prism. The refracted ray reaches the right face of the prism and refracts as it emerges out of the prism. The emerging ray makes an angle of theta with the normal to the right face.
94. If the apex angle \(\displaystyle ϕ\) in the previous problem is \(\displaystyle 20.0°\) and \(\displaystyle n=1.50\), what is the value of \(\displaystyle α\)?
95. The light incident on polarizing sheet \(\displaystyle P_1\) is linearly polarized at an angle of \(\displaystyle 30.0°\) with respect to the transmission axis of \(\displaystyle P_1\). Sheet \(\displaystyle P_2\) is placed so that its axis is parallel to the polarization axis of the incident light, that is, also at \(\displaystyle 30.0°\) with respect to \(\displaystyle P_1\).
(a) What fraction of the incident light passes through \(\displaystyle P_1\)?
(b) What fraction of the incident light is passed by the combination?
(c) By rotating \(\displaystyle P_2\), a maximum in transmitted intensity is obtained. What is the ratio of this maximum intensity to the intensity of transmitted light when \(\displaystyle P_2\) is at \(\displaystyle 30.0°\) with respect to \(\displaystyle P_1\)?
96. Prove that if I is the intensity of light transmitted by two polarizing filters with axes at an angle \(\displaystyle θ\) and \(\displaystyle I'\) is the intensity when the axes are at an angle \(\displaystyle 90.0°−θ\), then \(\displaystyle I+I'=I_0\), the original intensity. (Hint: Use the trigonometric identities \(\displaystyle cos90.0°−θ=sinθ\) and \(\displaystyle cos^2θ+sin^2θ=1\).)


