Chapter 15.1 Energy Changes in Chemical Reactions
- Page ID
- 42025
Learning Objectives
- To understand the concept of energy and its various forms.
- To learn the relationship between energy, work, and heat.
In this section, we describe forms of energy and discuss the relationship between energy, heat, and work.
Forms of Energy
Sources of energy include electrical, nuclear, and chemical. Electrical energy results from the flow of electrically charged particles, either ions or electrons, in one direction under the influence of electrical or magnetic fields. Nuclear is the energy holding the nucleus of atoms together and can be released or absorbed by nuclear reactions. These reactions can transmute the nucleus, changing either the mass number or the atomic number of the nucleus. Similarly, chemical energy is the energy stored in molecular bonds. In a chemical reaction bonds are broken and formed. Breaking bonds requires energy, making bonds produces energy.
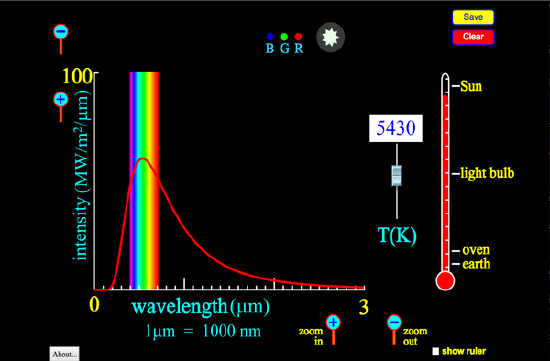
Types of energy include radiant, thermal, kinetic and potential energy. When charged particles move they emit electromagnetic radiation which we call radiant energy. This also includes quantum state changes in atoms and molecules which result in the emission/absorption of light. Any solid or liquid above absolute zero also emits radiant energy, called black body radiation, driven by internal motion of electrons, molecules or nuclei. This average energy and the distribution of potential and kinetic energies is characterized by the temperature of the black body and the motion is described as thermal . The intensity is governed by the Stefan-Boltzmann law, where E is the energy emitted per unit surface area.
\( E = \sigma T^{4} \tag{15.1.1} \)
The nature of this spectrum can be investigated using the following applet from PhET (you may need JAVA to see this)
Figure 15.1.1: An applet from PhET demonstrating the spectral distribution of black body emission as a function of temperature The envelope of the solar spectrum is a black body spectrum of about 5500 K with sharp lines characteristic of atomic spectra, such as the lines of the hydrogen atomic spectrum. Radiant energy spans the spectrum from X-ray to microwave and beyond.
Kinetic energy is due to the motion of an object. The energy tied up in chemical bonds is a form of potential energy which can be released when the bonds are broken in a reaction and the energy is converted into thermal energy, e.g. randomly directed kinetic energy. Chemical energy can also be converted to radiant energy; one common example is the light emitted by fireflies, which is produced from a chemical reaction.
Energy can be converted from one form to another or from one object to another. For example, when you climb a ladder to a high diving board, your body uses chemical energy produced by the combustion of organic molecules. As you climb, the chemical energy is converted to mechanical work to overcome the force of gravity. When you reach the top, your potential energy with respect to the water is increased, and when you dive off that potential energy is converted to kinetic energy as you move towards the water.
Although energy can be converted from one form to another, the total amount of energy in the universe remains constant. This is known as the Law of Conservation of EnergyThe total amount of energy in the universe remains constant. Energy can be neither created nor destroyed, but it can be converted from one form to another. If thermal energy is exchanged in any part of the process the Law of Conservation of Energy is also known as the First Law of Thermodynamics.
Energy, Work, and Heat
One definition of energy is the capacity to do work. The easiest form of work to visualize is mechanical workThe energy required to move an object a distance d when opposed by a force F, ( Figure 15.1.2, which is the energy required to move an object a distance d when opposed by a force F, such as gravity:
\( \begin{matrix}
work &=&force\times distance \\
w & = & Fd
\end{matrix} \tag{15.1.2} \)
Consider the mechanical work required for you to lift a barbell. Energy is expended to overcome the force of gravity. The amount of work done (w) and thus the energy required depends on three things: (1) the height the barbell is lifted to (the distance d); (2) the mass, which must be raised that distance against the downward acceleration due to gravity; and (3) the details of how you lift the barbell.

Figure 15.1.2 An Example of Mechanical Work One form of energy is mechanical work, the energy required to move an object of mass m a distance d when opposed by a force F, such as gravity.
Defining heat and thermal energy is a bit more complex. To start we will take a molecular viewpoint using the kinetic theory of gases as explained in Section 6.6. For an ideal gas the total internal energy is the sum of the kinetic energies of all of the molecules Per mole we showed in Section 6.6 that the energy E is related to the temperature T by
\( E = \dfrac{3}{2}RT \tag{15.1.3} \)
Rearranging Equation 15.1.3, we find that the temperature of an ideal gas is related to the average kinetic energy of an individual molecule by
\( T = \dfrac{1}{3R}Mv_{rms}^{2} \tag{15.1.4} \)
where R, the gas constant, is 8.314 J/mole-K and M is the molar mass of the gas molecules. From this, the temperature of the gas is directly proportional to the average kinetic energy.
For a real gas where the molecules attract each other, the thermal energy would be the sum of all of the kinetic energy plus the energy associated with the molecular attraction. A liquid would be the same, except that the potential energy associated with the molecular attraction would exceed the kinetic energy associated with the moving molecules (otherwise the liquid would turn into a gas).
The energy associated with the internal motions and bonding of the constituent atoms, nuclei and electrons is the internal energy
In contrast, heat (q)Thermal energy that can be transformed from an object at one temperature to an object at another temperature. is thermal energy that is transferred from an object at one temperature to an object at another temperature. The net transfer of thermal energy stops when the two objects reach the same temperature.
Temperature is related to heat flow by the Zeroth Law of Thermodynamics which states that if two bodies are in thermodynamic equilibrium with a third one, they are in thermodynamic equilibrium with each other. At equilibrium there will be no transfer of heat between the three bodies and they will all be at the same temperature. If we use a thermometer as the third body, the temperature registered by the thermometer will be the same for the two other bodies because they are all in thermodynamic equilibrium with each other.
In Section 6.6 we discussed how to use the kinetic theory to determine the total internal energy of a gas. For more complex systems this can be done using Statistical Mechanics which allows calculation of the distribution of energy among molecules in gases, liquids and solids. Thermodynamics does not allow calculation of internal energy but it does allow measuring changes in internal energy.
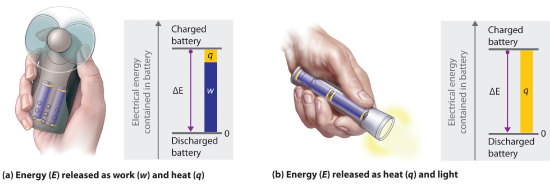
The internal energy of an object can be changed only by the transfer of energy to or from another object. Consider, for example, the chemical energy stored in a fully charged battery. As shown in Figure 15.1.3 , this energy can be used primarily to perform work (e.g., run an electric fan) or to generate light and heat (e.g., illuminating a light bulb). When the battery is fully discharged in either case, the total change in energy is the same, even though the fraction released as work or heat will vary depending on whether you are using an LED (less heat generated) or an incandescent bulb (heating the bulb filament by passing a current through it generates blackbody radiation). The sum of the heat produced and the work performed equals the change in energy (ΔE):
\( \begin{matrix}
Energy \; Change (\Delta E) & = & work + heat \\
\Delta E & = & q + w
\end{matrix} \tag{15.1.5} \)
This is the First Law of Thermodynamics. Energy can be transferred only in the form of heat, work performed on or by an object, or some combination of heat and work. The total change of energy is equal to the sum of the total heat transferred and work done. Heat added to the system is positive and heat taken away from the system is negative. Work done on the system is positive and work the system does is negative.
Figure 15.1.3 Energy Transfer: Discharging a fully charged battery releases the same amount of energy whether the battery is used to run a fan (a) or illuminate a light bulb (b). In (a), most of the energy is used to perform work, which turns the blades of the fan and thus moves the air; only a small portion of the energy is released as heat by the electric motor. In (b), all the energy is released as heat and light; no work is done.
In the next section we will discuss the difference between thermodynamic quantities that are properties of the state that a body is in. That means that to calculate the change in internal energy, ΔE, for some process it is not necessary to know how the changes have occurred but simply what the initial and final states are. The internal energy, E, and the change of internal energy in any process, ΔE, are called state functions.
Because work occurs only when an object, such as a person, or a substance, such as water, moves against an opposing force, work requires that a system and its surroundings be connected. In contrast, the flow of heat, the transfer of energy due to differences in temperature between two objects, represents a thermal connection between a system and its surroundings. This connection can also involve radiative transfer, as the transfer of energy from the Sun to the Earth. Thus doing work causes a physical displacement, whereas the flow of heat causes a temperature change. The units of work and heat must be the same because both processes result in the transfer of energy. In the SI system, those units are joules (J), the same unit used for energy. There is no difference between an energy change brought about by doing work on a system and an equal energy change brought about by heating it.
The quantity of work, w and heat, q, in any process are determined by the details of how the work is done, for example, was the work done at constant pressure, was heat flow between the surroundings allowed or not, was the temperature held constant or not. The heat and work in any process depend on the details, and heat and work are called path functions.
The differential form of the First Law of Thermodynamics is
\( \begin{matrix}
Energy \; Change (dE) & = & work + heat \\
dE & = & δq + δw
\end{matrix} \tag{15.1.6} \)
where dE indicates that energy is a perfect differential and δq and δw are inexact differentials. The differential form of fundamental equations such as the First Law is discussed in detail by Andreana Rosniks at another ChemWiki page, and will also be treated in this and the next chapter.
Energy is an extensive property of matter—for example, the amount of thermal energy in an object is proportional to both its mass and its temperature. A water heater that holds 150 L of water at 50°C contains much more thermal energy than does a 1 L pan of water at 50°C. Similarly, a bomb contains much more chemical energy than does a firecracker. We now present a more detailed description of kinetic and potential energy.
Because all forms of energy can be interconverted, energy in any form can be expressed using the same units as kinetic energy. The SI unit of energy, the joule (J), named after the British physicist James Joule (1818–1889). A joule is defined as 1 kilogram·meter2/second2 (kg·m2/s2). Because a joule is such a small quantity of energy, chemists usually express energy in kilojoules (1 kJ = 103 J).
Kinetic Energy
The kinetic energy of an object is related to its mass m and velocity v:
\( KE = \frac{1}{2} mv^{2} \tag{15.1.7} \)
PV Work
There are many kinds of work, including mechanical work, electrical work, and work against a gravitational or a magnetic field. Here we will consider only mechanical work, focusing on the work done during changes in the pressure or the volume of a gas. To describe this pressure–volume work (PV work), we will use such imaginary oddities as frictionless pistons, which involve no component of resistance, and ideal gases, which have no attractive or repulsive interactions.
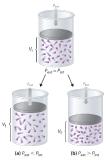
Imagine an ideal gas, confined by a frictionless piston, with internal pressure Pint and initial volume Vi (Figure 15.1.4). If Pext = Pint, the system is at equilibrium; the piston does not move, and no work is done. If the external pressure on the piston (Pext) is less than Pint, however, then the ideal gas inside the piston will expand, forcing the piston to perform work on its surroundings; that is, the final volume (Vf) will be greater than Vi. If Pext > Pint, then the gas will be compressed, and the surroundings will perform work on the system.
\( w =Fd= P_{ext} A d h \tag{15.1.8} \)
Figure 15.1.4 PV Work Using a frictionless piston, if the external pressure is less than Pint (a), the ideal gas inside the piston will expand, forcing the piston to perform work on its surroundings. The final volume (Vf) will be greater than Vi. Alternatively, if the external pressure is greater than Pint (b), the gas will be compressed, and the surroundings will perform work on the system.
The change in the volume of the cylinder (dV) as the piston moves a distance d is dV = Adh, as shown in Figure 15.1.4. The work performed is thus
\( w = P_{ext} dV \tag{15.1.9} \)
The units of work obtained using this definition are correct for energy: pressure is force per unit area (newton/m2) and volume has units of cubic meters, so
\( w=\dfrac{F}{A}d V = \dfrac{newton}{m^{2}}\times m^{3}= newton\times m = Joule\tag{15.1.10} \)
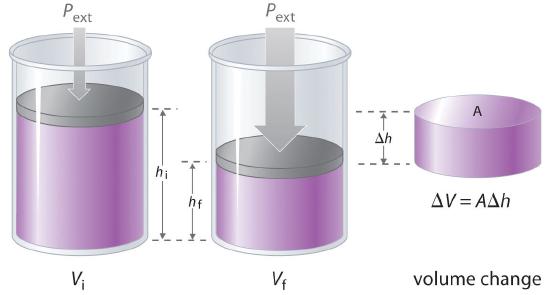
Figure 15.1.6 Work Performed with a Change in Volume The change in the volume (ΔV) of the cylinder housing a piston is ΔV = AΔh as the piston moves. The work performed by the surroundings on the system as the piston moves inward is given by w = PextΔV.
If we use atmospheres for P and liters for V, we obtain units of L·atm for work. These units correspond to units of energy, as shown in the different values of the ideal gas constant R:
\( R= \dfrac{0.08206 \; L \cdot \; atm}{mol\cdot K}= \dfrac{8.314 \; J}{mol\cdot K} \)
Thus 0.08206 L·atm = 8.314 J and 1 L·atm = 101.3 J. (For more information on the ideal gas law, see Chapter 6.)
Whether work is defined as having a positive sign or a negative sign is a matter of convention.Chemists, define heat flow from a system to its surroundings as negative. Using that same sign convention, we define work done by a system on its surroundings as having a negative sign because it results in a transfer of energy from a system to its surroundings.This is an arbitrary convention and one that is not universally used. Some engineering disciplines are more interested in the work done on the surroundings than in the work done by the system and therefore use the opposite convention. Because ΔV > 0 for an expansion, Equation 15.1.9 must be written with a negative sign to describe PV work done by the system as negative:
\( w = - P_{ext} \Delta V \tag{15.1.10} \)
The work done by a gas expanding against an external pressure is therefore negative, corresponding to work done by a system on its surroundings. Conversely, when a gas is compressed by an external pressure, ΔV < 0 and the work is positive because work is being done on a system by its surroundings.
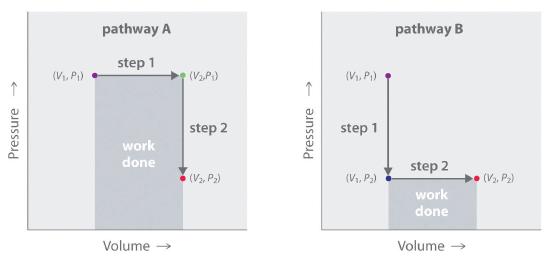
In contrast to internal energy, work is not a state function. We can see this by examining Figure 15.1.7, in which two different, two-step pathways take a gaseous system from an initial state to a final state with corresponding changes in temperature. In pathway A, the volume of a gas is initially increased while its pressure stays constant (step 1); then its pressure is decreased while the volume remains constant (step 2). In pathway B, the order of the steps is reversed. The temperatures, pressures, and volumes of the initial and final states are identical in both cases, but the amount of work done, indicated by the shaded areas in the figure, is substantially different. As we can see, the amount of work done depends on the pathway taken from (V1, P1) to (V2, P2), which means that work is not a state function.
Note the Pattern
Internal energy is a state function, whereas work is not.
Figure 15.1.7 Work Is Not a State Function In pathway A, the volume of a gas is initially increased while its pressure stays constant (step 1). Its pressure is then decreased while the volume remains constant (step 2). Pathway B reverses these steps. Although (V1, P1) and (V2, P2) are identical in both cases, the amount of work done (shaded area) depends on the pathway taken.
Note the Pattern
The units of energy are the same for all forms of energy.
Energy can also be expressed in the non-SI units of calories (cal)A non-SI unit of energy: 1 cal = 4.184 J exactly., where 1 cal was originally defined as the amount of energy needed to raise the temperature of exactly 1 g of water from 14.5°C to 15.5°C.We specify the exact temperatures because the amount of energy needed to raise the temperature of 1 g of water 1°C varies slightly with elevation. To three significant figures, however, this amount is 1.00 cal over the temperature range 0°C–100°C. The name is derived from the Latin calor, meaning “heat.” Although energy may be expressed as either calories or joules, calories were defined in terms of heat, whereas joules were defined in terms of motion. Because calories and joules are both units of energy, however, the calorie is now defined in terms of the joule:
\( 1\;cal = 4.184\; J exactly \tag{15.1.11a} \)
\( 1\;J = 0.2390 \; cal \tag{15.1.11b} \)
In this text, we will use the SI units—joules (J) and kilojoules (kJ). Engineers, of course, often use calories and (shudder) British thermal units (BTU) and other customary energy units
Example 15.1.1
- If the mass of a baseball is 149 g, what is the kinetic energy of a fastball clocked at 100 mi/h?
Given: mass and velocity or height
Asked for: kinetic energy
Strategy:
Use Equation 15.1.7 to calculate the kinetic energy
Solution:
-
The kinetic energy of an object is given by 1/2 mv2 In this case, we know both the mass and the velocity, but we must convert the velocity to SI units and then plug the answer into the formulat for kinetic energy
Key Equations
general definition of work
Equation 15.1.2: w = Fd
relationship between energy, heat, and work
Equation 15.1.5: ΔE = q + w
kinetic energy
Equation 15.1.7: KE = 1/2 mv2
Pressure volume work
Equation 15.1.9: \( w = - P_{ext} d V \)
Summary
Thermochemistry is a branch of chemistry that qualitatively and quantitatively describes the energy changes that occur during chemical reactions. Energy is the capacity to do work. Mechanical work is the amount of energy required to move an object a given distance when opposed by a force. Thermal energy is due to the random motions of atoms, molecules, or ions in a substance. The temperature of an object is a measure of the amount of thermal energy it contains. Heat (q) is the transfer of thermal energy from a hotter object to a cooler one. Energy can take many forms; most are different varieties of potential energy (PE), energy caused by the relative position or orientation of an object. Kinetic energy (KE) is the energy an object possesses due to its motion. Energy can be converted from one form to another, but the law of conservation of energy states that energy can be neither created nor destroyed.
When thermal energy is transferred the law of conservation of energy is called the first law of thermodynamics.
The most common units of energy are the joule (J), defined as 1 (kg·m2)/s2, and the calorie, defined as the amount of energy needed to raise the temperature of 1 g of water by 1°C (1 cal = 4.184 J).
Key Takeaway
- All forms of energy can be interconverted. Three things can change the energy of an object: the transfer of heat, work performed on or by an object, or some combination of heat and work.
Conceptual Problems
-
What is the relationship between mechanical work and energy?
-
Does a person with a mass of 50 kg climbing a height of 15 m do work? Explain your answer. Does that same person do work while descending a mountain?
-
If a person exerts a force on an immovable object, does that person do work? Explain your answer.
-
Explain the differences between electrical energy, nuclear energy, and chemical energy.
-
The chapter describes thermal energy, radiant energy, electrical energy, nuclear energy, and chemical energy. Which form(s) of energy are represented by each of the following?
- sunlight
- the energy produced by a cathode ray tube, such as that found in a television
- the energy emitted from radioactivity
- the energy emitted from a burning candle
- the energy associated with a steam engine
- the energy emitted by a cellular phone
- the energy associated with a stick of dynamite
-
Describe the various forms of energy that are interconverted when a flashlight is switched on.
-
Describe the forms of energy that are interconverted when the space shuttle lifts off.
-
Categorize each of the following as representing kinetic energy or potential energy.
- the energy associated with a laptop computer sitting on the edge of a desk
- shoveling snow
- water pouring out of a fire hydrant
- the energy released by an earthquake
- the energy in a volcano about to erupt
- the energy associated with a coiled spring
-
Are the units for potential energy the same as the units for kinetic energy? Can an absolute value for potential energy be obtained? Explain your answer.
-
Categorize each of the following as representing kinetic energy or potential energy.
- water cascading over Niagara Falls
- a beaker balanced on the edge of a sink
- the energy released during a mudslide
- rollerblading
- the energy in a block of ice on a rooftop before a thaw
-
Why does hammering a piece of sheet metal cause the metal to heat up?
Answers
-
-
-
Technically, the person is not doing any work, since the object does not move.
-
-
-
-
-
-
-
-
The kinetic energy of the hammer is transferred to the metal.
Numerical Problems
Please be sure you are familiar with the topics discussed in Essential Skills 4 (Section 5.6 "Essential Skills 4") before proceeding to the Numerical Problems.
-
Describe the mathematical relationship between (a) the thermal energy stored in an object and that object’s mass and (b) the thermal energy stored in an object and that object’s temperature.
-
How much energy (in kilojoules) is released or stored when each of the following occurs?
- A 230 lb football player is lifted to a height of 4.00 ft.
- An 11.8 lb cat jumps from a height of 6.50 ft.
- A 3.75 lb book falls off of a shelf that is 5.50 ft high.
-
Calculate how much energy (in kilojoules) is released or stored when each of the following occurs:
- A 130 lb ice skater is lifted 7.50 ft off the ice.
- A 48 lb child jumps from a height of 4.0 ft.
- An 18.5 lb light fixture falls from a 10.0 ft ceiling.
-
A car weighing 1438 kg falls off a bridge that is 211 ft high. Ignoring air resistance, how much energy is released when the car hits the water?
-
A 1 tn roller coaster filled with passengers reaches a height of 28 m before accelerating downhill. How much energy is released when the roller coaster reaches the bottom of the hill? Assume no energy is lost due to friction.
Answers
-
- The thermal energy content of an object is directly proportional to its mass.
- The thermal energy content of an object is directly proportional to its temperature.
-
-
- 1.3 kJ stored
- 0.26 kJ released
- 0.251 kJ released
-
-
250 kJ released
Contributors
- Anonymous
Modified by Joshua Halpern (Howard University), Scott Sinex, and Scott Johnson (PGCC)
Blackbody Applet from PheT