6.1: Distribution Functions for Gas-velocity Components
- Last updated
- Save as PDF
- Page ID
- 206340
In Chapter 2, we assume that all of the molecules in a gas move with the same speed and use a simplified argument to conclude that this speed depends only on temperature. We now recognize that the individual molecules in a gas sample have a wide range of speeds; the velocities of gas molecules must be described by a distribution function. It is true, however, that the average speed depends only on temperature.
James Clerk Maxwell was the first to derive the distribution function for gas velocities. He did it about 1860. We follow Maxwell’s argument. For a molecule moving in three dimensions, there are three velocity components. Maxwell’s argument uses only one assumption: the speed of a gas molecule is independent of the direction in which it is moving. Equivalently, we can say that the components of the velocity of a gas molecule are independent of one another; knowing the value of one component of a molecule’s velocity does not enable us to infer anything about the values of the other two components. When we use Cartesian coordinates, Maxwell’s assumptionMaxwell’s assumption means also that the same mathematical model must describe the distribution of each of the velocity components.
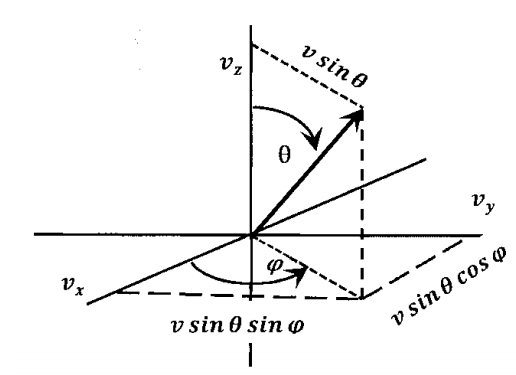
Since the velocity of a gas molecule has three components, we must treat the velocity distribution as a function of three random variables. To understand how this can be done, let us consider how we might find probability distribution functions for velocity components. We need to consider both spherical and Cartesian coordinate systems.
Let us suppose that we are able to measure the Cartesian-coordinate components \(v_x\), \(v_y\), and \(v_z\) of the velocities of a large number of randomly selected gas molecules in a particular constant-temperature sample. Then we can transform each set of Cartesian components to spherical-coordinate velocity covelocity componentsmponents \(v\), \(\theta\), and \(\varphi\). We imagine accumulating the results of these measurements in a table like Table 1. As a practical matter, of course, we cannot make the measurements to complete such a table. However, there is no doubt that, at every instant, every gas molecule can be characterized by a set of such velocity components; the values exist, even if we cannot measure them. We imagine that we have such data only as a way to clarify the properties of the distribution functions that we need.
Table 1. Molecular Velocity Components
| Molecule Number | \({\boldsymbol{v}}_{\boldsymbol{x}}\) | \({\boldsymbol{v}}_{\boldsymbol{x}}\) | \({\boldsymbol{v}}_{\boldsymbol{x}}\) | v | \(\boldsymbol{\theta }\) | \(\boldsymbol{\varphi }\) |
|---|---|---|---|---|---|---|
| 1 | \(v_x\left(1\right)\) | \(v_y\left(1\right)\) | \(v_z\left(1\right)\) | \(v\left(1\right)\) | \(\theta \left(1\right)\) | \(\varphi \left(1\right)\) |
| 2 | \(v_x\left(2\right)\) | \(v_y\left(2\right)\) | \(v_z\left(2\right)\) | \(v\left(2\right)\) | \(\theta \left(2\right)\) | \(\varphi \left(2\right)\) |
| 3 | \(v_x\left(3\right)\) | \(v_y\left(3\right)\) | \(v_z\left(3\right)\) | \(v\left(3\right)\) | \(\theta \left(3\right)\) | \(\varphi \left(3\right)\) |
| 4 | \(v_x\left(4\right)\) | \(v_y\left(4\right)\) | \(v_z\left(4\right)\) | \(v\left(4\right)\) | \(\theta \left(4\right)\) | \(\varphi \left(4\right)\) |
| … | … | … | … | … | … | … |
| \(N\) | \(v_x\left(N\right)\) | \(v_x\left(N\right)\) | \(v_z\left(N\right)\) | \(v\left(N\right)\) | \(\theta \left(N\right)\) | \(\varphi \left(N\right)\) |
These data have several important features. The scalar velocity, \(v\), ranges from 0 to \(+\infty\); \(v_x\), \(v_y\), and \(v_z\) range from \(-\infty\) to \(+\infty\). In §2, we see that \(\theta\) varies from 0 to \(\pi\); and \(\varphi\) ranges from 0 to \(2\pi\). Each column represents data sampled from the distribution of the corresponding random variable. In Chapter 3, we find that we can use such data to find mathematical models for such distributions. Here, we can find mathematical models for the cumulative distribution functions \(f_x\left(v_x\right)\), \(f_y\left(v_y\right)\), and \(f_z\left(v_z\right)\). We can approximate the graph of \(f_x\left(v_x\right)\) by plotting the rank probability of \(v_x\) versus \(v_x\). We expect this plot to be sigmoid; at any \(v_x\), the slope of this plot is the probability-density function, \({df_x\left(v_x\right)}/{dv_x}\). The probability density function for \(v_x\) depends only on \(v_x\), because the value measured for \(v_x\) is independent of the values measured for \(v_y\) and \(v_z\). However, by Maxwell’s assumption, the functions describing the distribution of \(v_y\) and \(v_z\) are the same as those describing the distribution of \(v_x\). While redundant, it is convenient to introduce additional symbols to represent these probability density functions. We define \({\rho }_x\left(v_x\right)={df_x\left(v_x\right)}/{dv_x}\), \({\rho }_y\left(v_y\right)={df_y\left(v_y\right)}/{dv_y}\), and \({\rho }_z\left(v_z\right)={df_z\left(v_z\right)}/{dv_z}\).
When we find these one-dimensional distribution functions by modeling the experimental data in this way, each \(v_x\) datum that we use in our analysis comes from an observation on a molecule and is associated with particular \(v_y\) and \(v_z\) values. These values of \(v_y\) and \(v_z\) can be anything from \(-\infty\) to \(+\infty\). This is a significant point. The functions \(f_x\left(v_x\right)\) and \({df_x\left(v_x\right)}/{dv_x}\) are independent of \(v_y\) and \(v_z\). We can also say that \({df_x\left(v_x\right)}/{dv_x}\) describes the distribution of \(v_x\) when \(v_y\) and \(v_z\) are averaged over all the values it is possible for them to have.
To clarify this, let us consider another cumulative probability distribution function, \(f_{xyz}\left(v_x,v_y,v_z\right)\), which is just the fraction of all molecules whose respective Cartesian velocity components are less than \(v_x\), \(v_y\), \(v_z\). Since \(f_x\left(v_x\right)\), \(f_y\left(v_y\right)\), and \(f_z\left(v_z\right)\) are the fractions whose components are less than \(v_x\), \(v_y\), and \(v_z\), respectively, their product is equal to \(f_{xyz}\left(v_x,v_y,v_z\right)\) We have \(f_{xyz}\left(v_x,v_y,v_z\right)=f_x\left(v_x\right)f_y\left(v_y\right)f_z\left(v_z\right)\). For the velocity of a randomly selected molecule, \(\left(v^*_x,v^*_y,v^*_z\right)\), to be included in the fraction represented by \(f_{xyz}\left(v_x,v_y,v_z\right)\), the velocity must be in the particular range \({ + \mathrm{\infty }\mathrm{<}v}^{\mathrm{*}}_x\mathrm{<}v_x\), \( + \mathrm{\infty }\mathrm{<}v^{\mathrm{*}}_y\mathrm{<}v_y\), and \({ + \mathrm{\infty }\mathrm{<}v}^{\mathrm{*}}_z\mathrm{<}v_z\).
However, for a velocity \(v^*_x\) to be included in \(f_x\left(v_x\right)\), we must have \(v^*_x<v_x\), \(v^*_y<\infty\), and \(v^*_z<\infty\); that is, the components \(v^*_y\) and \(v^*_z\) can have any values. Since the probability that \(v_x\), \(v_y\), and \(v_z\) satisfy \(v^*_x<v_x\), \(v^*_y<v_y\), and \(v^*_z<v_z\) is
\[\begin{aligned} P\left(v^*_x<v_x,v^*_y<v_y,v^*_z<v_z\right) & = f_{xyz} \left(v_x,v_y,v_z \right) \\ ~ & = f_x (v_x)f_y(v_y)f_z(v_z) \end{aligned} \nonumber \]
the probability that \(v^*_x\) is included in \(f_x\left(v_x\right)\) becomes
\[ \begin{aligned} P\left(v^*_x<v_x,v^*_y< \infty, v_z^* < \infty \right) & = f_{xyz} \left( v_x, \infty, \infty \right) \\ ~ & = f_x \left( v_x \right) f_y \left( \infty \right) f_z \left( \infty \right) \\ ~ & = f_x \left( v_x \right) \end{aligned} \nonumber \]
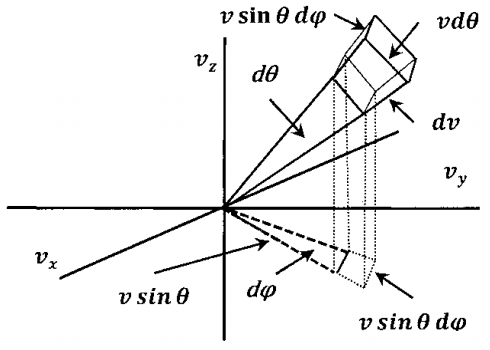
For our purposes, we need to be able to express the probability that the velocity lies within any range of velocities. Let us use \(\mathrm{\textrm{ʋ}}\) to designate a particular “volume” region in velocity space and use \(P\left(\mathrm{\textrm{ʋ}}\right)\) to designate the probability that the velocity of a randomly selected molecule is in this region. When we let ʋ be the region in velocity space in which \(x\)-components lie between \(v_x\)
and \(v_x+dv_x\), \(y\)-components lie between \(v_y\), and \(v_y+dv_y\), and \(z\)-components lie between \(v_z\) and \(v_z+dv_z\), \(dP\left(\textrm{ʋ}\right)\) denotes the probability that the velocity of a randomly chosen molecule,\(\ \left(v^*_x,v^*_y,v^*_z\right)\), satisfies the conditions \(v_x<v^*_x<v_x+dv_x\), \(v_y<v^*_y<v_y+dv_y\), and \(v_z<v^*_z<v_z+dv_z\).
\(dP\left(\textrm{ʋ}\right)\) is an increment of probability. The dependence of \(\ dP\left(\textrm{ʋ}\right)\) on \(v_x\), \(v_y\), \(v_z\), \({dv}_x\), \(dv_y\), and \(dv_z\)can be made explicit by introducing a new function, \(\rho \left(v_x,v_y,v_z\right)\), defined by
\[dP\left(\textrm{ʋ}\right)=\rho \left(v_x,v_y,v_z\right)dv_xdv_ydv_z \nonumber \]
Since \(dv_xdv_ydv_z\) is the volume available in velocity space for velocities whose \(x\)-components are between \(v_x\) and \(v_x+dv_x\), whose \(y\)-components are between \(v_y\), and \(v_y+dv_y\), and whose \(z\)-components are between \(v_z\) and \(v_z+dz\), we see that \(\rho \left(v_x,v_y,v_z\right)\) is a probability density function in three dimensions. The value of \(\rho \left(v_x,v_y,v_z\right)\) is the probability, per unit volume in velocity space, that a molecule has the velocity \(\left(v_x,v_y,v_z\right)\). For any velocity, \(\left(v_x,v_y,v_z\right)\), there is a value of \(\rho \left(v_x,v_y,v_z\right)\); this value is just a number. If we want the probability of finding a velocity within some small volume of velocity space around \(\left(v_x,v_y,v_z\right)\), we can find it by multiplying \(\rho \left(v_x,v_y,v_z\right)\) by this volume.
From the one-dimensional probability-density functions, the probability that the \(x\)-component of a molecular velocity lies between \(v_x\) and \(v_x+dv_x\), is just \(\left({{df}_x\left(v_x\right)}/{dv_x}\right)dv_x\), whatever the values of \(v_y\) and \(v_z\). The probability that the \(y\)-component lies between \(v_y\) and \(v_y+dv_y\), is just \(\left({{df}_y\left(v_y\right)}/{dv_y}\right)dv_y\), whatever the values of \(v_x\) and \(v_z\). The probability that the \(z\)-component lies between \(v_z\) and \(v_z+dv_z\), is just \(\left({df_z\left(v_z\right)}/{dv_z}\right)dv_z\), whatever the values of \(v_x\) and \(v_y\). When we interpret Maxwell’s assumption to mean that these are independent probabilities, the probability that all three conditions are realized simultaneously is
\[dP\left(\textrm{ʋ}\right)=\left(\frac{df_x\left(v_x\right)}{dv_x}\right)\left(\frac{df_y\left(v_y\right)}{{dv}_y}\right)\left(\frac{{df}_z\left(v_z\right)}{{dv}_z}\right)dv_xdv_ydv_z=\rho \left(v_x,v_y,v_z\right)dv_xdv_ydv_z \nonumber \]
Evidently, the product of these three one-dimensional probability densities is the three-dimensional probability density. We have \[\rho \left(v_x,v_y,v_z\right)=\left(\frac{df_x\left(v_x\right)}{dv_x}\right)\left(\frac{df_y\left(v_y\right)}{{dv}_y}\right)\left(\frac{{df}_z\left(v_z\right)}{{dv}_z}\right)={\rho }_x\left(v_x\right){\rho }_y\left(v_y\right){\rho }_z\left(v_z\right) \nonumber \]
From Maxwell’s assumption, we have derived the conclusion that \(\rho \left(v_x,v_y,v_z\right)\) can be expressed as a product of the one-dimensional probability densities \(\left({df\left(v_x\right)}/{dv_x}\right)dv_x\), \(\left({df\left(v_y\right)}/{dv_y}\right)dv_y\), and \(\left({df\left(v_z\right)}/{dv_z}\right)dv_z\). Since these are probability densities, we have
\[\int^{\infty }_{-\infty }{\left(\frac{{df}_x\left(v_x\right)}{dv_x}\right)}dv_x=\int^{\infty }_{-\infty }{\left(\frac{{df}_y\left(v_y\right)}{dv_y}\right)}dv_y=\int^{\infty }_{-\infty }{\left(\frac{{df}_z\left(v_z\right)}{dv_z}\right)}dv_z=1 \nonumber \] and \[\mathop{\int\!\!\!\!\int\!\!\!\!\int}\nolimits^{\infty }_{-\infty }{\rho \left(v_x,v_y,v_z\right){dv}_xdv_y}dv_z=1 \nonumber \]
Moreover, because the Cartesian coordinates differ from one another only in orientation, \(\left({df\left(v_x\right)}/{dv_x}\right)dv_x\), \(\left({df\left(v_y\right)}/{dv_y}\right)dv_y\), and \(\left({df\left(v_z\right)}/{dv_z}\right)dv_z\) must all be the same function.
To summarize the development above, we define \(\rho \left(v_x,v_y,v_z\right)\) independently of \({df_x\left(v_x\right)}/{dv_x}\), \({df_y\left(v_y\right)}/{dv_y}\), and \({df_z\left(v_z\right)}/{dv_z}\). Then, from Maxwell’s assumption that the three one-dimensional probabilities are independent, we find \[\rho \left(v_x,v_y,v_z\right)=\left(\frac{df_x\left(v_x\right)}{dv_x}\right)\left(\frac{df_y\left(v_y\right)}{{dv}_y}\right)\left(\frac{{df}_z\left(v_z\right)}{{dv}_z}\right) \nonumber \] \[={\rho }_x\left(v_x\right){\rho }_y\left(v_y\right){\rho }_z\left(v_z\right) \nonumber \]
Alternatively, we could take Maxwell’s assumption to be that the three-dimensional probability density function is expressible as a product of three one-dimensional probability densities:
\[\rho \left(v_x,v_y,v_z\right) ={\rho }_x\left(v_x\right){\rho }_y\left(v_y\right){\rho }_z\left(v_z\right) \nonumber \]
In this case, the relationships of \({\rho }_x\left(v_x\right)\), \({\rho }_y\left(v_y\right)\), and \({\rho }_z\left(v_z\right)\), to the one-dimensional cumulative probabilities (\(f_x\left(v_x\right)\), etc.) must be deduced from the properties of \(\rho \left(v_x,v_y,v_z\right)\). As emphasized above, our deduction of \(f_x\left(v_x\right)\) from experimental data uses \(v_x\) values that are associated with all possible values of \(v_y\) and \(v_z\). That is, what we determine in our (hypothetical) experiment is
\[ \begin{aligned} f_x\left(v_x\right) & =\int^{v_x}_{v_x=-\infty}{\mathop{\int\!\!\!\!\int}\nolimits^{\infty}_{v_{y,z} = -\infty }{\rho \left(v_x,v_y,v_z\right){dv}_xdv_ydv_z}} \\ & =\int^{v_x}_{-\infty} \rho_x \left(v_x\right)dv_x\int^{\infty}_{-\infty} \rho_y \left(v_y\right) dv_y\int^{\infty}_{-\infty} \rho_z \left(v_z\right) dv_z \\ & =\int^{v_x}_{-\infty} \rho_x \left(v_x\right) dv_x \end{aligned} \nonumber \]
from which it follows that
\[\frac{{df}_x\left(v_x\right)}{{dv}_x}={\rho }_x\left(v_x\right) \nonumber \]