2.1: A History of Atomic Theory
- Page ID
- 98684
Skills to Develop
By the end of this section, you will be able to:
- State the postulates of Dalton’s atomic theory
- Use postulates of Dalton’s atomic theory to explain the laws of definite and multiple proportions
- Outline milestones in the development of modern atomic theory
- Summarize and interpret the results of the experiments of Thomson, Millikan, and Rutherford
A Video Introduction to Atomic Theory through the Nineteenth Century From Crash Course Chemistry
Video \(\PageIndex{1}\): Lavoisier's discovery of The Law of Conservation of Matter led to the Laws of Definite and Multiple Proportions and eventually Dalton's Atomic Theory.
Atomic Theory through the Nineteenth Century
The earliest recorded discussion of the basic structure of matter comes from ancient Greek philosophers, the scientists of their day. In the fifth century BC, Leucippus and Democritus argued that all matter was composed of small, finite particles that they called atomos, a term derived from the Greek word for “indivisible.” They thought of atoms as moving particles that differed in shape and size, and which could join together. Later, Aristotle and others came to the conclusion that matter consisted of various combinations of the four “elements”—fire, earth, air, and water—and could be infinitely divided. Interestingly, these philosophers thought about atoms and “elements” as philosophical concepts, but apparently never considered performing experiments to test their ideas.
The Aristotelian view of the composition of matter held sway for over two thousand years, until English schoolteacher John Dalton helped to revolutionize chemistry with his hypothesis that the behavior of matter could be explained using an atomic theory. First published in 1807, many of Dalton’s hypotheses about the microscopic features of matter are still valid in modern atomic theory. Here are the postulates of Dalton’s atomic theory.
- Matter is composed of exceedingly small particles called atoms. An atom is the smallest unit of an element that can participate in a chemical change.
- An element consists of only one type of atom, which has a mass that is characteristic of the element and is the same for all atoms of that element (Figure \(\PageIndex{1}\)). A macroscopic sample of an element contains an incredibly large number of atoms, all of which have identical chemical properties.
- Atoms of one element differ in properties from atoms of all other elements.
- A compound consists of atoms of two or more elements combined in a small, whole-number ratio. In a given compound, the numbers of atoms of each of its elements are always present in the same ratio (Figure \(\PageIndex{2}\)).
- Atoms are neither created nor destroyed during a chemical change, but are instead rearranged to yield substances that are different from those present before the change (Figure \(\PageIndex{3}\)).

Figure \(\PageIndex{1}\): A pre-1982 copper penny (left) contains approximately 3 \(\times\) 1022 copper atoms (several dozen are represented as brown spheres at the right), each of which has the same chemical properties. (credit: modification of work by “slgckgc”/Flickr)

Figure \(\PageIndex{2}\): Copper(II) oxide, a powdery, black compound, results from the combination of two types of atoms—copper (brown spheres) and oxygen (red spheres)—in a 1:1 ratio. (credit: modification of work by “Chemicalinterest”/Wikimedia Commons)
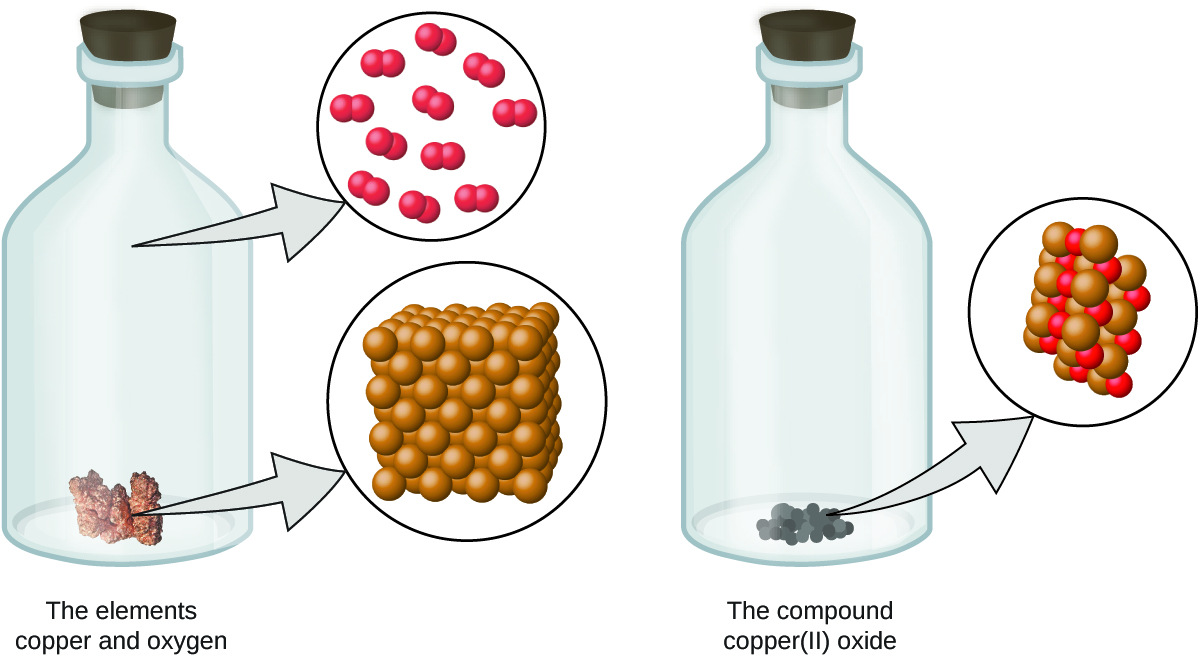
Figure \(\PageIndex{3}\): When the elements copper (a shiny, red-brown solid, shown here as brown spheres) and oxygen (a clear and colorless gas, shown here as red spheres) react, their atoms rearrange to form a compound containing copper and oxygen (a powdery, black solid). (credit copper: modification of work by http://images-of-elements.com/copper.php).
Dalton’s atomic theory provides a microscopic explanation of the many macroscopic properties of matter that you’ve learned about. For example, if an element such as copper consists of only one kind of atom, then it cannot be broken down into simpler substances, that is, into substances composed of fewer types of atoms. And if atoms are neither created nor destroyed during a chemical change, then the total mass of matter present when matter changes from one type to another will remain constant (the law of conservation of matter (or mass)).
Want to learn more about the Law of Conservation of Mass?
Video \(\PageIndex{2}\): "We are made of star stuff" - Carl Sagan.
Example \(\PageIndex{1}\): Testing Dalton’s Atomic Theory
In the following drawing, the green spheres represent atoms of a certain element. The purple spheres represent atoms of another element. If the spheres touch, they are part of a single unit of a compound. Does the following chemical change represented by these symbols violate any of the ideas of Dalton’s atomic theory? If so, which one?
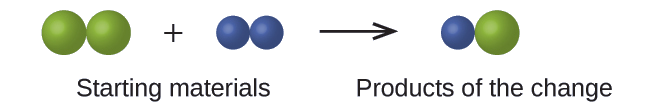
Solution
The starting materials consist of two green spheres and two purple spheres. The products consist of only one green sphere and one purple sphere. This violates Dalton’s postulate that atoms are neither created nor destroyed during a chemical change, but are merely redistributed. (In this case, atoms appear to have been destroyed.)
Exercise \(\PageIndex{1}\)
In the following drawing, the green spheres represent atoms of a certain element. The purple spheres represent atoms of another element. If the spheres touch, they are part of a single unit of a compound. Does the following chemical change represented by these symbols violate any of the ideas of Dalton’s atomic theory? If so, which one

- Answer
-
The starting materials consist of four green spheres and two purple spheres. The products consist of four green spheres and two purple spheres. This does not violate any of Dalton’s postulates: Atoms are neither created nor destroyed, but are redistributed in small, whole-number ratios.
Dalton knew of the experiments of French chemist Joseph Proust, who demonstrated that all samples of a pure compound contain the same elements in the same proportion by mass. This statement is known as the law of definite proportions or the law of constant composition. The suggestion that the numbers of atoms of the elements in a given compound always exist in the same ratio is consistent with these observations. For example, when different samples of isooctane (a component of gasoline and one of the standards used in the octane rating system) are analyzed, they are found to have a carbon-to-hydrogen mass ratio of 5.33:1, as shown in Table \(\PageIndex{1}\).
| Sample | Carbon | Hydrogen | Mass Ratio |
|---|---|---|---|
| A | 14.82 g | 2.78 g | \(\mathrm{\dfrac{14.82\: g\: carbon}{2.78\: g\: hydrogen}=\dfrac{5.33\: g\: carbon}{1.00\: g\: hydrogen}}\) |
| B | 22.33 g | 4.19 g | \(\mathrm{\dfrac{22.33\: g\: carbon}{4.19\: g\: hydrogen}=\dfrac{5.33\: g\: carbon}{1.00\: g\: hydrogen}}\) |
| C | 19.40 g | 3.64 g | \(\mathrm{\dfrac{19.40\: g\: carbon}{3.63\: g\: hydrogen}=\dfrac{5.33\: g\: carbon}{1.00\: g\: hydrogen}}\) |
It is worth noting that although all samples of a particular compound have the same mass ratio, the converse is not true in general. That is, samples that have the same mass ratio are not necessarily the same substance. For example, there are many compounds other than isooctane that also have a carbon-to-hydrogen mass ratio of 5.33:1.00.
Dalton also used data from Proust, as well as results from his own experiments, to formulate another interesting law. The law of multiple proportions states that when two elements react to form more than one compound, a fixed mass of one element will react with masses of the other element in a ratio of small, whole numbers. For example, copper and chlorine can form a green, crystalline solid with a mass ratio of 0.558 g chlorine to 1 g copper, as well as a brown crystalline solid with a mass ratio of 1.116 g chlorine to 1 g copper. These ratios by themselves may not seem particularly interesting or informative; however, if we take a ratio of these ratios, we obtain a useful and possibly surprising result: a small, whole-number ratio.
\[\mathrm{\dfrac{\dfrac{1.116\: g\: Cl}{1\: g\: Cu}}{\dfrac{0.558\: g\: Cl}{1\: g\: Cu}}=\dfrac{2}{1}}\]
This 2-to-1 ratio means that the brown compound has twice the amount of chlorine per amount of copper as the green compound.
This can be explained by atomic theory if the copper-to-chlorine ratio in the brown compound is 1 copper atom to 2 chlorine atoms, and the ratio in the green compound is 1 copper atom to 1 chlorine atom. The ratio of chlorine atoms (and thus the ratio of their masses) is therefore 2 to 1 (Figure \(\PageIndex{4}\)).
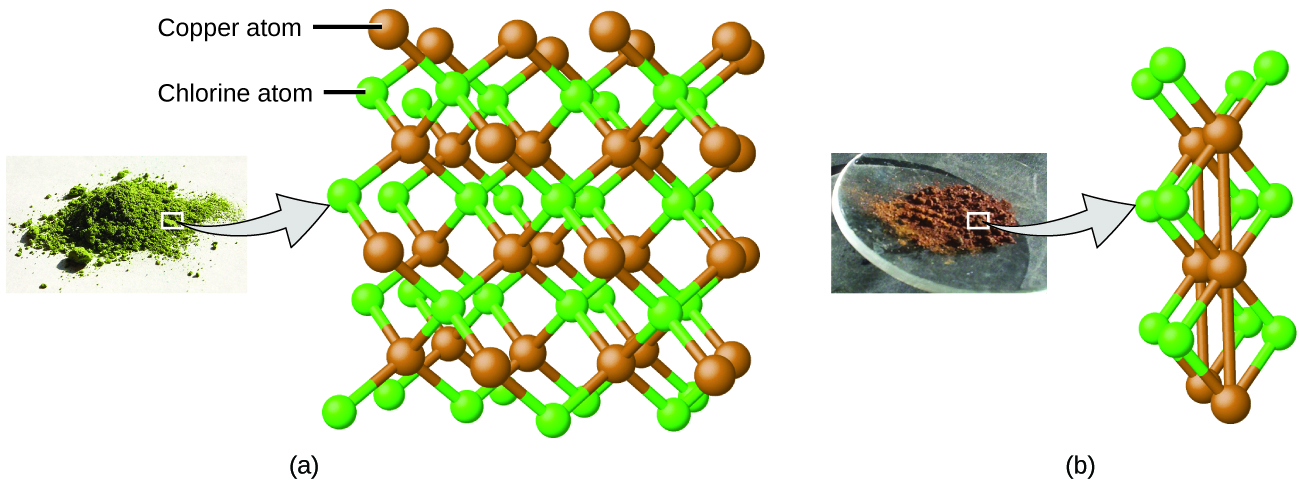
Figure \(\PageIndex{4}\): Compared to the copper chlorine compound in (a), where copper is represented by brown spheres and chlorine by green spheres, the copper chlorine compound in (b) has twice as many chlorine atoms per copper atom. (credit a: modification of work by “Benjah-bmm27”/Wikimedia Commons; credit b: modification of work by “Walkerma”/Wikimedia Commons)
Example \(\PageIndex{2}\): Laws of Definite and Multiple Proportions
A sample of compound A (a clear, colorless gas) is analyzed and found to contain 4.27 g carbon and 5.69 g oxygen. A sample of compound B (also a clear, colorless gas) is analyzed and found to contain 5.19 g carbon and 13.84 g oxygen. Are these data an example of the law of definite proportions, the law of multiple proportions, or neither? What do these data tell you about substances A and B?
Solution
In compound A, the mass ratio of carbon to oxygen is:
\[\mathrm{\dfrac{1.33\: g\: O}{1\: g\: C}} \nonumber\]
In compound B, the mass ratio of carbon to oxygen is:
\[\mathrm{\dfrac{2.67\: g\: O}{1\: g\: C}} \nonumber\]
The ratio of these ratios is:
\[\mathrm{\dfrac{\dfrac{1.33\: g\: O}{1\: g\: C}}{\dfrac{2.67\: g\: O}{1\: g\: C}}=\dfrac{1}{2}} \nonumber\]
This supports the law of multiple proportions. This means that A and B are different compounds, with A having one-half as much carbon per amount of oxygen (or twice as much oxygen per amount of carbon) as B. A possible pair of compounds that would fit this relationship would be A = CO2 and B = CO.
Exercise \(\PageIndex{2}\)
A sample of compound X (a clear, colorless, combustible liquid with a noticeable odor) is analyzed and found to contain 14.13 g carbon and 2.96 g hydrogen. A sample of compound Y (a clear, colorless, combustible liquid with a noticeable odor that is slightly different from X’s odor) is analyzed and found to contain 19.91 g carbon and 3.34 g hydrogen. Are these data an example of the law of definite proportions, the law of multiple proportions, or neither? What do these data tell you about substances X and Y?
- Answer
-
In compound X, the mass ratio of carbon to hydrogen is \(\mathrm{\dfrac{14.13\: g\: C}{2.96\: g\: H}}\).
In compound Y, the mass ratio of carbon to oxygen is \(\mathrm{\dfrac{19.91\: g\: C}{3.34\: g\: H}}\).
The ratio of these ratios is
\[\mathrm{\dfrac{\dfrac{14.13\: g\: C}{2.96\: g\: H}}{\dfrac{19.91\: g\: C}{3.34\: g\: H}}=\dfrac{4.77\: g\: C/g\: H}{5.96\: g\: C/g\: H}=0.800=\dfrac{4}{5}}. \nonumber\]
This small, whole-number ratio supports the law of multiple proportions. This means that X and Y are different compounds.
In the two centuries since Dalton developed his ideas, scientists have made significant progress in furthering our understanding of atomic theory. Much of this came from the results of several seminal experiments that revealed the details of the internal structure of atoms. Here, we will discuss some of those key developments, with an emphasis on application of the scientific method, as well as understanding how the experimental evidence was analyzed. While the historical persons and dates behind these experiments can be quite interesting, it is most important to understand the concepts resulting from their work.
Atomic Theory after the Nineteenth Century
If matter were composed of atoms, what were atoms composed of? Were they the smallest particles, or was there something smaller? In the late 1800s, a number of scientists interested in questions like these investigated the electrical discharges that could be produced in low-pressure gases, with the most significant discovery made by English physicist J. J. Thomson using a cathode ray tube. This apparatus consisted of a sealed glass tube from which almost all the air had been removed; the tube contained two metal electrodes. When high voltage was applied across the electrodes, a visible beam called a cathode ray appeared between them. This beam was deflected toward the positive charge and away from the negative charge, and was produced in the same way with identical properties when different metals were used for the electrodes. In similar experiments, the ray was simultaneously deflected by an applied magnetic field, and measurements of the extent of deflection and the magnetic field strength allowed Thomson to calculate the charge-to-mass ratio of the cathode ray particles. The results of these measurements indicated that these particles were much lighter than atoms (Figure \(\PageIndex{1}\)).
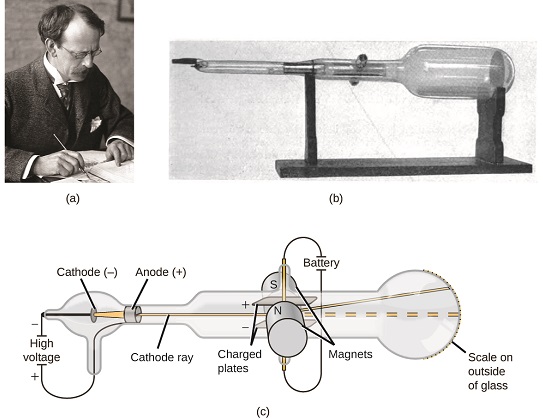
Figure \(\PageIndex{5}\): (a) J. J. Thomson produced a visible beam in a cathode ray tube. (b) This is an early cathode ray tube, invented in 1897 by Ferdinand Braun. (c) In the cathode ray, the beam (shown in yellow) comes from the cathode and is accelerated past the anode toward a fluorescent scale at the end of the tube. Simultaneous deflections by applied electric and magnetic fields permitted Thomson to calculate the mass-to-charge ratio of the particles composing the cathode ray. (credit a: modification of work by Nobel Foundation; credit b: modification of work by Eugen Nesper; credit c: modification of work by “Kurzon”/Wikimedia Commons).
Based on his observations, here is what Thomson proposed and why: The particles are attracted by positive (+) charges and repelled by negative (−) charges, so they must be negatively charged (like charges repel and unlike charges attract); they are less massive than atoms and indistinguishable, regardless of the source material, so they must be fundamental, subatomic constituents of all atoms. Although controversial at the time, Thomson’s idea was gradually accepted, and his cathode ray particle is what we now call an electron, a negatively charged, subatomic particle with a mass more than one thousand-times less that of an atom. The term “electron” was coined in 1891 by Irish physicist George Stoney, from “electric ion.”
In 1909, more information about the electron was uncovered by American physicist Robert A. Millikan via his “oil drop” experiments. Millikan created microscopic oil droplets, which could be electrically charged by friction as they formed or by using X-rays. These droplets initially fell due to gravity, but their downward progress could be slowed or even reversed by an electric field lower in the apparatus. By adjusting the electric field strength and making careful measurements and appropriate calculations, Millikan was able to determine the charge on individual drops (Figure \(\PageIndex{2}\)).
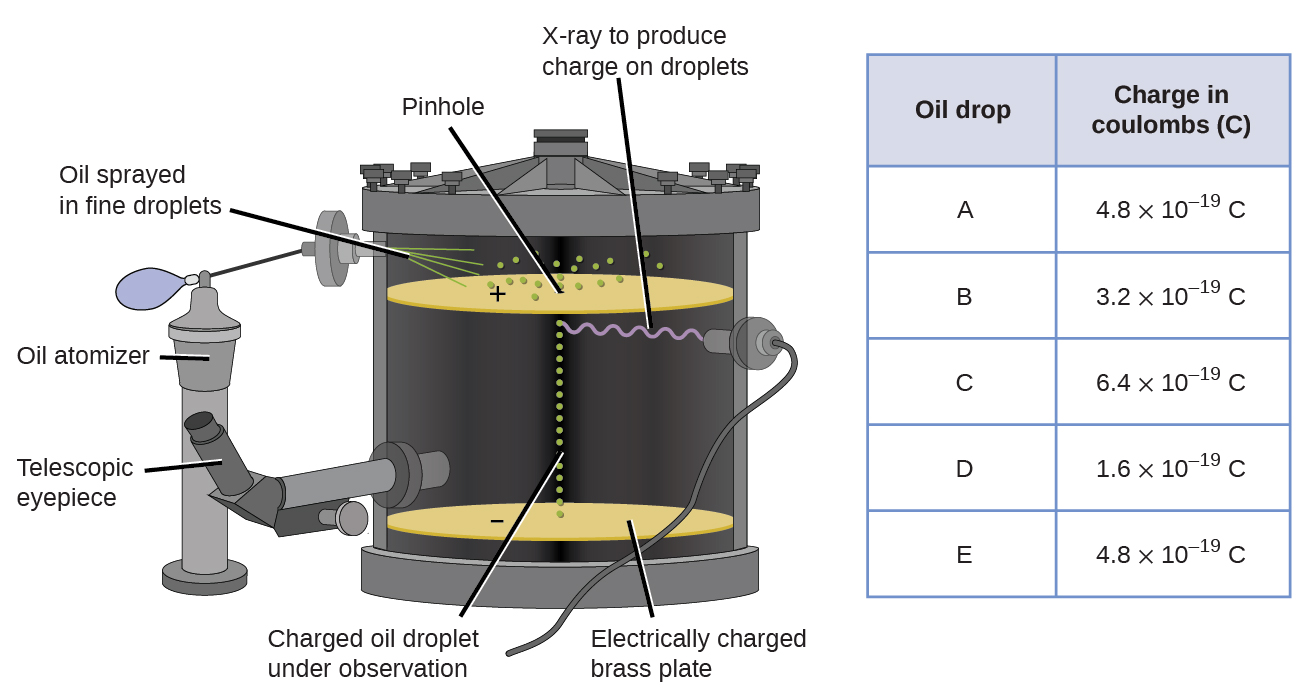
Figure \(\PageIndex{6}\): Millikan’s experiment measured the charge of individual oil drops. The tabulated data are examples of a few possible values.
Looking at the charge data that Millikan gathered, you may have recognized that the charge of an oil droplet is always a multiple of a specific charge, 1.6 \(\times\) 10−19 C. Millikan concluded that this value must therefore be a fundamental charge—the charge of a single electron—with his measured charges due to an excess of one electron (1 times 1.6 \(\times\) 10−19 C), two electrons (2 times 1.6 \(\times\) 10−19 C), three electrons (3 times 1.6 \(\times\) 10−19 C), and so on, on a given oil droplet. Since the charge of an electron was now known due to Millikan’s research, and the charge-to-mass ratio was already known due to Thomson’s research (1.759 \(\times\) 1011 C/kg), it only required a simple calculation to determine the mass of the electron as well.
\[\mathrm{Mass\: of\: electron=1.602\times 10^{-19}\:\cancel{C}\times \dfrac{1\: kg}{1.759\times 10^{11}\:\cancel{C}}=9.107\times 10^{-31}\:kg} \tag{2.3.1}\]
Scientists had now established that the atom was not indivisible as Dalton had believed, and due to the work of Thomson, Millikan, and others, the charge and mass of the negative, subatomic particles—the electrons—were known. However, the positively charged part of an atom was not yet well understood. In 1904, Thomson proposed the “plum pudding” model of atoms, which described a positively charged mass with an equal amount of negative charge in the form of electrons embedded in it, since all atoms are electrically neutral. A competing model had been proposed in 1903 by Hantaro Nagaoka, who postulated a Saturn-like atom, consisting of a positively charged sphere surrounded by a halo of electrons (Figure \(\PageIndex{3}\)).
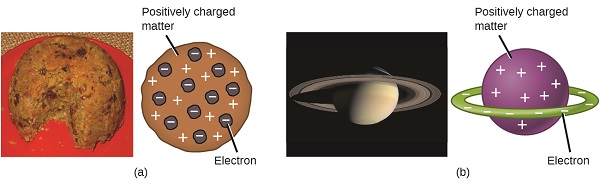
Figure \(\PageIndex{7}\): (a) Thomson suggested that atoms resembled plum pudding, an English dessert consisting of moist cake with embedded raisins (“plums”). (b) Nagaoka proposed that atoms resembled the planet Saturn, with a ring of electrons surrounding a positive “planet.” (credit a: modification of work by “Man vyi”/Wikimedia Commons; credit b: modification of work by “NASA”/Wikimedia Commons).
The next major development in understanding the atom came from Ernest Rutherford, a physicist from New Zealand who largely spent his scientific career in Canada and England. He performed a series of experiments using a beam of high-speed, positively charged alpha particles (α particles) that were produced by the radioactive decay of radium; α particles consist of two protons and two neutrons (you will learn more about radioactive decay in the chapter on nuclear chemistry). Rutherford and his colleagues Hans Geiger (later famous for the Geiger counter) and Ernest Marsden aimed a beam of α particles, the source of which was embedded in a lead block to absorb most of the radiation, at a very thin piece of gold foil and examined the resultant scattering of the α particles using a luminescent screen that glowed briefly where hit by an α particle.
What did they discover? Most particles passed right through the foil without being deflected at all. However, some were diverted slightly, and a very small number were deflected almost straight back toward the source (Figure \(\PageIndex{4}\)). Rutherford described finding these results: “It was quite the most incredible event that has ever happened to me in my life. It was almost as incredible as if you fired a 15-inch shell at a piece of tissue paper and it came back and hit you”1 (p. 68).
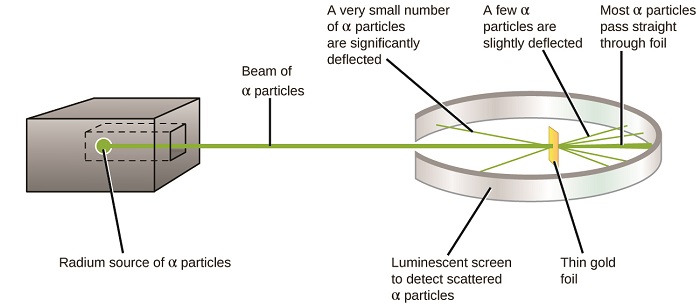
Figure \(\PageIndex{8}\): Geiger and Rutherford fired α particles at a piece of gold foil and detected where those particles went, as shown in this schematic diagram of their experiment. Most of the particles passed straight through the foil, but a few were deflected slightly and a very small number were significantly deflected.
Here is what Rutherford deduced: Because most of the fast-moving α particles passed through the gold atoms undeflected, they must have traveled through essentially empty space inside the atom. Alpha particles are positively charged, so deflections arose when they encountered another positive charge (like charges repel each other). Since like charges repel one another, the few positively charged α particles that changed paths abruptly must have hit, or closely approached, another body that also had a highly concentrated, positive charge. Since the deflections occurred a small fraction of the time, this charge only occupied a small amount of the space in the gold foil. Analyzing a series of such experiments in detail, Rutherford drew two conclusions:
- The volume occupied by an atom must consist of a large amount of empty space.
- A small, relatively heavy, positively charged body, the nucleus, must be at the center of each atom.
This analysis led Rutherford to propose a model in which an atom consists of a very small, positively charged nucleus, in which most of the mass of the atom is concentrated, surrounded by the negatively charged electrons, so that the atom is electrically neutral (Figure \(\PageIndex{5}\)).
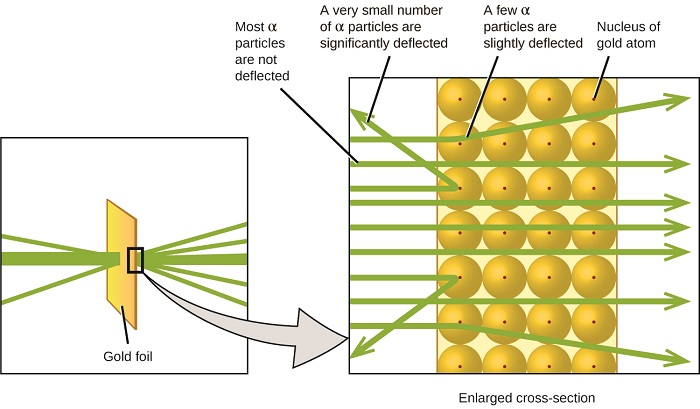
Figure \(\PageIndex{9}\): The α particles are deflected only when they collide with or pass close to the much heavier, positively charged gold nucleus. Because the nucleus is very small compared to the size of an atom, very few α particles are deflected. Most pass through the relatively large region occupied by electrons, which are too light to deflect the rapidly moving particles.
After many more experiments, Rutherford also discovered that the nuclei of other elements contain the hydrogen nucleus as a “building block,” and he named this more fundamental particle the proton, the positively charged, subatomic particle found in the nucleus. With one addition, which you will learn next, this nuclear model of the atom, proposed over a century ago, is still used today.
Another important finding was the discovery of isotopes. During the early 1900s, scientists identified several substances that appeared to be new elements, isolating them from radioactive ores. For example, a “new element” produced by the radioactive decay of thorium was initially given the name mesothorium. However, a more detailed analysis showed that mesothorium was chemically identical to radium (another decay product), despite having a different atomic mass. This result, along with similar findings for other elements, led the English chemist Frederick Soddy to realize that an element could have types of atoms with different masses that were chemically indistinguishable. These different types are called isotopes—atoms of the same element that differ in mass. Soddy was awarded the Nobel Prize in Chemistry in 1921 for this discovery.
One puzzle remained: The nucleus was known to contain almost all of the mass of an atom, with the number of protons only providing half, or less, of that mass. Different proposals were made to explain what constituted the remaining mass, including the existence of neutral particles in the nucleus. As you might expect, detecting uncharged particles is very challenging, and it was not until 1932 that James Chadwick found evidence of neutrons, uncharged, subatomic particles with a mass approximately the same as that of protons. The existence of the neutron also explained isotopes: They differ in mass because they have different numbers of neutrons, but they are chemically identical because they have the same number of protons. This will be explained in more detail later in this unit.
Video \(\PageIndex{2}\): An Introduction to Subatomic Particles
Summary
Video \(\PageIndex{3}\): A summary of discoveries in atomic theory.
Video \(\PageIndex{4}\): A different summary of discoveries in atomic theory.
The ancient Greeks proposed that matter consists of extremely small particles called atoms. Dalton postulated that each element has a characteristic type of atom that differs in properties from atoms of all other elements, and that atoms of different elements can combine in fixed, small, whole-number ratios to form compounds. Samples of a particular compound all have the same elemental proportions by mass. When two elements form different compounds, a given mass of one element will combine with masses of the other element in a small, whole-number ratio. During any chemical change, atoms are neither created nor destroyed.
Although no one has actually seen the inside of an atom, experiments have demonstrated much about atomic structure. Thomson’s cathode ray tube showed that atoms contain small, negatively charged particles called electrons. Millikan discovered that there is a fundamental electric charge—the charge of an electron. Rutherford’s gold foil experiment showed that atoms have a small, dense, positively charged nucleus; the positively charged particles within the nucleus are called protons. Chadwick discovered that the nucleus also contains neutral particles called neutrons. Soddy demonstrated that atoms of the same element can differ in mass; these are called isotopes.
Footnotes
- Ernest Rutherford, “The Development of the Theory of Atomic Structure,” ed. J. A. Ratcliffe, in Background to Modern Science, eds. Joseph Needham and Walter Pagel, (Cambridge, UK: Cambridge University Press, 1938), 61–74. Accessed September 22, 2014, https://ia600508.us.archive.org/3/it...e032734mbp.pdf.
Glossary
- Dalton’s atomic theory
- set of postulates that established the fundamental properties of atoms
- law of constant composition
- (also, law of definite proportions) all samples of a pure compound contain the same elements in the same proportions by mass
- law of multiple proportions
- when two elements react to form more than one compound, a fixed mass of one element will react with masses of the other element in a ratio of small whole numbers
- law of definite proportions
- (also, law of constant composition) all samples of a pure compound contain the same elements in the same proportions by mass
- alpha particle (α particle)
- positively charged particle consisting of two protons and two neutrons
- electron
- negatively charged, subatomic particle of relatively low mass located outside the nucleus
- isotopes
- atoms that contain the same number of protons but different numbers of neutrons
- neutron
- uncharged, subatomic particle located in the nucleus
- proton
- positively charged, subatomic particle located in the nucleus
- nucleus
- massive, positively charged center of an atom made up of protons and neutrons
Contributors
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).
- Adelaide Clark, Oregon Institute of Technology
- Crash Course Chemistry: Crash Course is a division of Complexly and videos are free to stream for educational purposes.
- TED-Ed’s commitment to creating lessons worth sharing is an extension of TED’s mission of spreading great ideas. Within TED-Ed’s growing library of TED-Ed animations, you will find carefully curated educational videos, many of which represent collaborations between talented educators and animators nominated through the TED-Ed website.

