3.6: Cycloalkanes and Ring Strain
- Last updated
- Save as PDF
- Page ID
- 182858
Learning Objective
- explain the partial rotation of carbon-carbon single bonds in rings
- explain ring strain and its relationship to cycloalkane stability
Cycloalkanes (aka Rings)
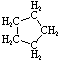
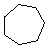
Cycloalkanes have one or more rings of carbon atoms. The simplest examples of this class consist of a single, unsubstituted carbon ring, and these form a homologous series similar to the unbranched alkanes. The IUPAC names of the first five members of this series are given in the following table. The last column gives the general formula for a cycloalkane of any size. If a simple unbranched alkane is converted to a cycloalkane two hydrogen atoms, one from each end of the chain, must be lost. Hence the general formula for a cycloalkane composed of n carbons is CnH2n. Although a cycloalkane has two fewer hydrogens than the equivalent alkane, each carbon is bonded to four other atoms so such compounds are still considered to be saturated with hydrogen.
| Name | Cyclopropane | Cyclobutane | Cyclopentane | Cyclohexane | Cycloheptane | Cycloalkane |
|---|---|---|---|---|---|---|
| Molecular Formula |
C3H6 | C4H8 | C5H10 | C6H12 | C7H14 | CnH2n |
| Structural Formula |
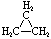 |
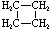 |
 |
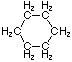 |
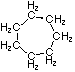 |
(CH2)n |
| Line Formula |
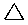 |
 |
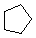 |
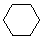 |
 |
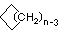 |
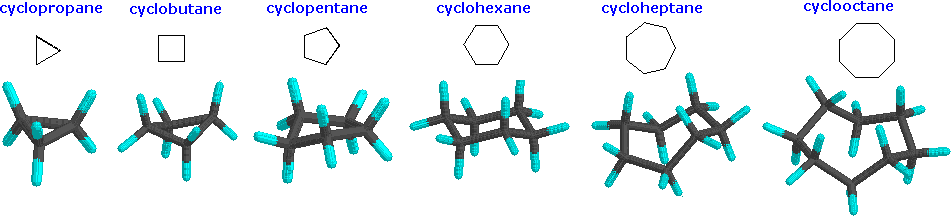
Although the customary line drawings of simple cycloalkanes are geometrical polygons, the actual shape of these compounds in most cases is very different. Cyclic systems are a little different from open-chain systems. In an open chain, any bond can be rotated 360 degrees, going through many different conformations. Complete rotation isn't possible in a cyclic system, because the parts that you would be trying to twist away from each other would still be connected together. Cyclic systems have fewer "degrees of freedom" than aliphatic systems; they have "restricted rotation". Because of the restricted rotation of cyclic systems, most of them have much more well-defined shapes than their aliphatic counterparts. Let's take a look at the basic shapes of some common rings. Many biologically important compounds are built around structures containing rings, so it's important that we become familiar with them. In nature, three- to six-membered rings are frequently encountered, so we'll focus on those.
The Baeyer Theory and the Experimental Evidence of Ring Strain
Many of the properties of cyclopropane and its derivatives are similar to the properties of alkenes. In 1890, the famous German organic chemist, A. Baeyer, suggested that cyclopropane and cyclobutane derivatives are different from cyclopentane and cyclohexane, because their C—C—C angles cannot have the tetrahedral value of 109.5°. At the same time, Baeyer hypothesized that the difficulties encountered in synthesizing cycloalkane rings from C7 upward was the result of the angle strain that would be expected if the large rings were regular planar polygons (see Table 12-3). Baeyer also believed that cyclohexane had a planar structure like that shown in Figure 12-2, which would mean that the bond angles would have to deviate 10.5° from the tetrahedral value. However, in 1895, the then unknown chemist H. Sachse suggested that cyclohexane exists in the strain-free chair and boat forms discussed in Section 12-3. This suggestion was not accepted at the time because it led to the prediction of several possible isomers for compounds such as chlorocyclohexane (cf. Exercise 12-4). The idea that such isomers might act as a single substance, as the result of rapid equilibration, seemed like a needless complication, and it was not until 1918 that E. Mohr proposed a definitive way to distinguish between the Baeyer and Sachse cyclohexanes. As will be discussed in Section 12-9, the result, now known as the Sachse-Mohr theory, was complete confirmation of the idea of nonplanar large rings.
| Compound | n | Angle Strain at each CH2 | Heat of Combustion ΔHo (kcal/mol) | Heat of Combustion ΔHo per CH2/N (kcal/mol) | Total Strain (kcal/mol) |
|---|---|---|---|---|---|
| ethene | 2 | 109.5 | 337.2 | 168.6 | 22.4 |
| cyclopropane | 3 | 49.5 | 499.9 | 166.6 | 27.7 |
| cyclobutane | 4 | 19.5 | 655.9 | 164.0 | 26.3 |
| cyclopentane | 5 | 1.5 | 793.4 | 158.7 | 6.5 |
| cyclohexane | 6 | 10.5 | 944.8 | 157.5 | 0.4 |
| cycloheptane | 7 | 19.1 | 1108.1 | 158.4 | 6.3 |
| cyclooctane | 8 | 25.5 | 1268.9 | 158.6 | 9.7 |
| cyclononane | 9 | 30.5 | 1429.5 | 158.8 | 12.9 |
| cyclodecane | 10 | 34.5 | 1586.1 | 158.6 | 12.1 |
| cyclopentadecane | 15 | 46.5 | 2362.5 | 157.5 | 1.5 |
| open chain alkane | 157.4 | - |
Ring Strain in Cycloalkanes
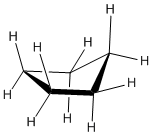
Ring Strain occurs because the carbons in cycloalkanes are sp3 hybridized, which means that they do not have the expected ideal bond angle of 109.5o ; this causes an increase in the potential energy because of the desire for the carbons to be at an ideal 109.5o. An example of ring strain can be seen in the diagram of cyclopropane below in which the bond angle is 60o between the carbons.
The reason for ring strain can be seen through the tetrahedral carbon model. The C-C-C bond angles in cyclopropane (diagram above) (60o) and cyclobutane (90o) are much different than the ideal bond angle of 109.5o. This bond angle causes cyclopropane and cyclobutane to have a high ring strain. However, molecules, such as cyclohexane and cyclopentane, would have a much lower ring strain because the bond angle between the carbons is much closer to 109.5o.
Below are some examples of cycloalkanes. Ring strain can be seen more prevalently in the cyclopropane and cyclobutane models
Below is a chart of cycloalkanes and their respective heats of combustion ( ΔHcomb). The ΔHcomb value increases as the number of carbons in the cycloalkane increases (higher membered ring), and the ΔHcomb/CH2 ratio decreases. The increase in ΔHcomb can be attributed to the greater amount of London Dispersion forces. However, the decrease in ΔHcomb/CH2can be attributed to a decrease in the ring strain.
Certain cycloalkanes, such as cyclohexane, deal with ring strain by forming conformers. A conformer is a stereoisomer in which molecules of the same connectivity and formula exist as different isomers, in this case, to reduce ring strain. The ring strain is reduced in conformers due to the rotations around the sigma bonds.
Other Types of Strain
There are many different types of strain that occur with cycloalkanes. In addition to ring strain, there is also transannular strain, eclipsing, or torsional strain and bond angle strain.Transannular strain exists when there is steric repulsion between atoms. Eclipsing (torsional) strain exists when a cycloalkane is unable to adopt a staggered conformation around a C-C bond, and bond angle strain is the energy needed to distort the tetrahedral carbons enough to close the ring. The presence of angle strain in a molecule indicates that there are bond angles in that particular molecule that deviate from the ideal bond angles required (i.e., that molecule has conformers).


Cyclopropane
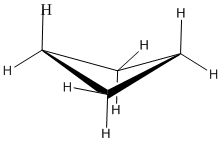
A three membered ring has no rotational freedom whatsoever, so the three carbon atoms in cyclopropane are all constrained to lie in the same plane at the corners of an equilateral triangle. The 60º bond angles are much smaller than the optimum 109.5º angles of a normal tetrahedral carbon atom, and the resulting angle strain dramatically influences the chemical behavior of this cycloalkane. Cyclopropane also suffers substantial eclipsing strain, since all the carbon-carbon bonds are fully eclipsed.
Furthermore, if you look at a model you will find that the neighboring C-H bonds (C-C bonds, too) are all held in eclipsed conformations.
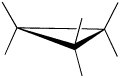
Cyclopropane is always at maximum torsional strain. This strain can be illustrated in a line drawing of cyclopropane as shown from the side. In this oblique view, the dark lines mean that those sides of the ring are closer to you.
However, the ring isn't big enough to introduce any steric strain, which does not become a factor until we reach six membered rings. Until that point, rings are not flexible enough for two atoms to reach around and bump into each other.
The really big problem with cyclopropane is that the C-C-C bond angles are all too small.
- All the carbon atoms in cyclopropane appear to be tetrahedral.
- These bond angles ought to be 109 degrees.
- The angles in an equilateral triangle are actually 60 degrees, about half as large as the optimum angle.
- This factor introduces a huge amount of strain in the molecule, called ring strain.
Cyclobutane
Cyclobutane is a four membered ring. In two dimensions, it is a square, with 90 degree angles at each corner. Cyclobutane reduces some bond-eclipsing strain by folding (the out-of-plane dihedral angle is about 25º), but the total eclipsing and angle strain remains high. Cyclopentane has very little angle strain (the angles of a pentagon are 108º), but its eclipsing strain would be large (about 10 kcal/mol) if it remained planar. Consequently, the five-membered ring adopts non-planar puckered conformations whenever possible.
However, in three dimensions, cyclobutane is flexible enough to buckle into a "butterfly" shape, relieving torsional strain a little bit. When it does that, the bond angles get a little worse, going from 90 degrees to 88 degrees.
In a line drawing, this butterfly shape is usually shown from the side, with the near edges drawn using darker lines.
- With bond angles of 88 rather than 109 degrees, cyclobutane has a lot of ring strain, but less than in cyclopropane.
- Torsional strain is still present, but the neighbouring bonds are not exactly eclipsed in the butterfly.
- Cyclobutane is still not large enough that the molecule can reach around to cause crowding. Steric strain is very low.
- Cyclobutanes are a little more stable than cyclopropanes and are also a little more common in nature.
Cyclopentane
Cyclopentanes are even more stable than cyclobutanes, and they are the second-most common paraffinic ring in nature, after cyclohexanes. In two dimensions, a cyclopentane appears to be a regular pentagon.
In three dimensions, there is enough freedom of rotation to allow a slight twist out of this planar shape. In a line drawing, this three-dimensional shape is drawn from an oblique view, just like cyclobutane.
- The ideal angle in a regular pentagon is about 107 degrees, very close to a tetrahedral bond angle.
- Cyclopentane distorts only very slightly into an "envelope" shape in which one corner of the pentagon is lifted up above the plane of the other four, and as a result, ring strain is entirely removed.
- The envelope removes torsional strain along the sides and flap of the envelope. However, the neighbouring carbons are eclipsed along the "bottom" of the envelope, away from the flap. There is still some torsional strain in cyclopentane.
- Again, there is no steric strain in this system.
Rings larger than cyclopentane would have angle strain if they were planar. However, this strain, together with the eclipsing strain inherent in a planar structure, can be relieved by puckering the ring. Cyclohexane is a good example of a carbocyclic system that virtually eliminates eclipsing and angle strain by adopting non-planar conformations. Cycloheptane and cyclooctane have greater strain than cyclohexane, in large part due to transannular crowding (steric hindrance by groups on opposite sides of the ring).
Exercise \(\PageIndex{1}\)
1. If cyclobutane were to be planar how many H-H eclipsing interactions would there be, and assuming 4 kJ/mol per H-H eclipsing interaction what is the strain on this “planar” molecule?
2. In the two conformations of cis-cyclopentane one is more stable than the other. Explain why this is.
- Answer
-
1. There are 8 eclipsing interactions (two per C-C bond). The extra strain on this molecule would be 32 kJ/mol (4 kJ/mol x 8).
2. The first conformation is more stable. Even though the methyl groups are cis in the model on the left, they are eclipsing due the conformation, therefore increasing the strain within the molecule.
Contributors and Attributions
Dr. Dietmar Kennepohl FCIC (Professor of Chemistry, Athabasca University)
Prof. Steven Farmer (Sonoma State University)
Chris P Schaller, Ph.D., (College of Saint Benedict / Saint John's University)
William Reusch, Professor Emeritus (Michigan State U.), Virtual Textbook of Organic Chemistry