5.2: The Electromagnetic Spectrum
- Page ID
- 204191
Learning Objectives
- Know the difference between wave and particle radiation
- Understand the relationships of wavelength, frequency, and energy
- Calculate frequency and wavelength of radiation
- Know the order of the electromagnetic spectrum (names, not numbers)
Roentgen, Becquerel and the Curies experimented with radiation. Using machines, Roengten's focused on the production X-rays, which is a wave-type of radiation. Unlike Roengten, Henri Becquerel studied the natural radioactivity of elements. His uranium experiments yielded the production of alpha (particle-type) and gamma (ray-type) radiations. Becquerel's two graduate students, Marie and Pierre Curie, isolated two radioactive elements. Both radium and polonium emit alpha and beta particles upon decay. In this section, wave form radiation will be explored. This type of radiation has an extremely wide range of wavelengths, frequencies, and energies.
Properties of Waves
A wave is a periodic oscillation that transmits energy through space. Anyone who has visited a beach or dropped a stone into a puddle has observed waves traveling through water (Figure \(\PageIndex{1}\)). These waves are produced when wind, a stone, or some other disturbance, such as a passing boat, transfers energy to the water, causing the surface to oscillate up and down as the energy travels outward from its point of origin. As a wave passes a particular point on the surface of the water, anything floating there moves up and down.
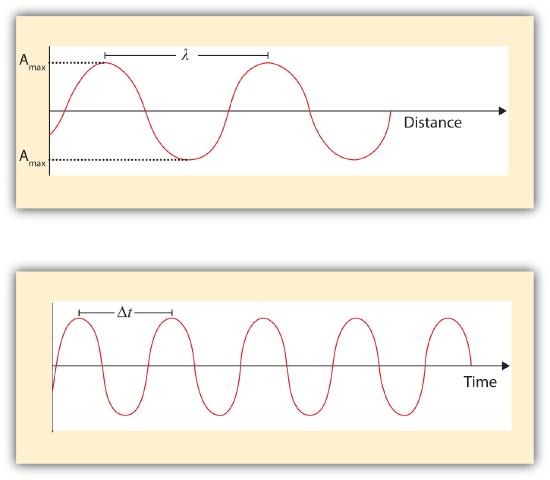
Waves have characteristic properties (Figure \(\PageIndex{1}\)). Waves are periodic, meaning, they repeat regularly in both space and time. The distance between two corresponding points in a wave—between the midpoints of two peaks, for example, or two troughs—is the wavelength (λ), distance between two corresponding points in a wave—between the midpoints of two peaks or two troughs. \(\lambda\) is the lowercase Greek lambda, and \(\nu\) is the lowercase Greek nu. Wavelengths are described by a unit of distance, typically meters. The frequency (ν) is the number of oscillations (i.e., of a wave) that pass a particular point in a given period of time. The unit for frequency is per second (1/s = s−1), which is equivalent to the SI unit of hertz (Hz). Amplitude, or vertical height of a wave, is defined as half the peak-to-trough. As the amplitude of a wave with a given frequency increases, so does its energy.
Electromagnetic Radiation
Energy that is transmitted, or radiated, through space in the form of periodic oscillations of electric and magnetic fields is known as electromagnetic radiation. (Figure \(\PageIndex{2}\)). Some forms of electromagnetic radiation are shown in Figure \(\PageIndex{4}\). In a vacuum, all forms of electromagnetic radiation—whether microwaves, visible light, or gamma rays—travel at the speed of light (c), which is the speed with which all forms of electromagnetic radiation travel in a vacuum, a fundamental physical constant with a value of 2.99792458 × 108 m/s (which is about 3.00 ×108 m/s or 1.86 × 105 mi/s). This is about a million times faster than the speed of sound.
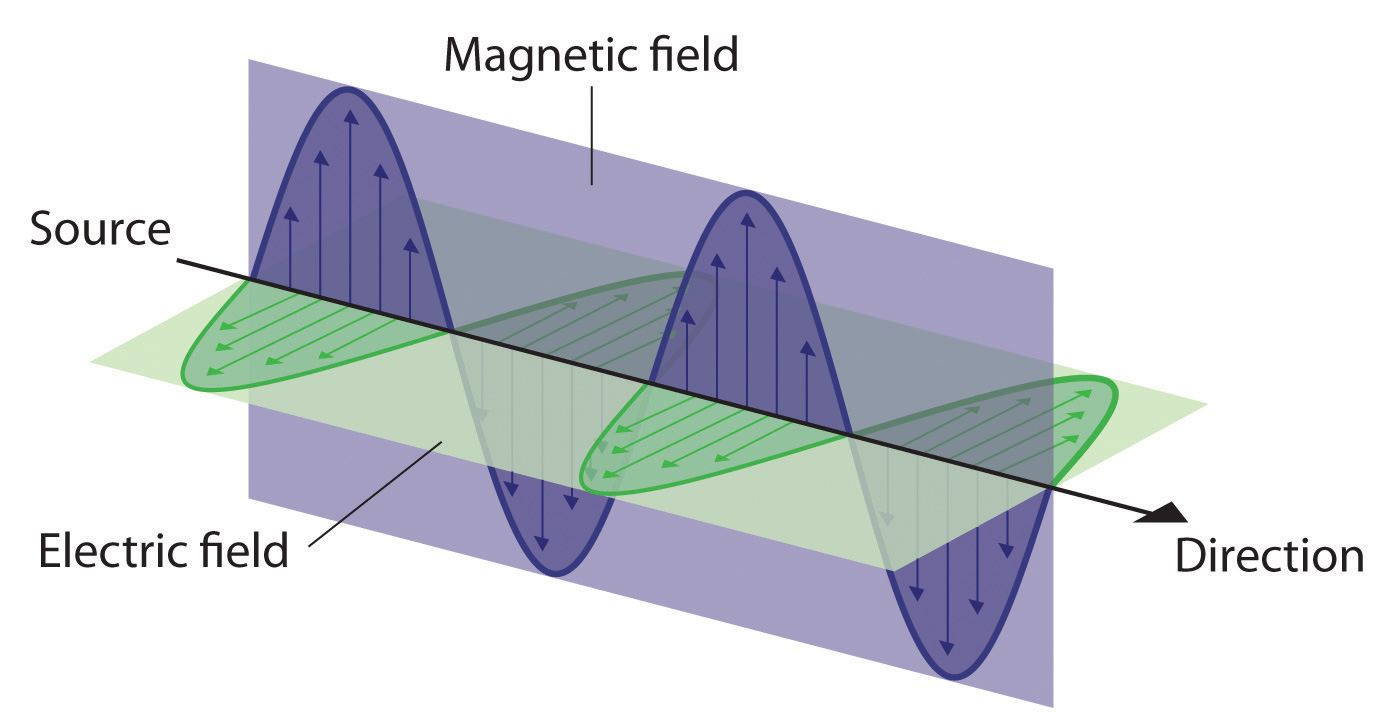
Because the various kinds of electromagnetic radiation all have the same speed (c), they differ in only wavelength and frequency. As shown in Figure \(\PageIndex{3}\) and Table \(\PageIndex{1}\), the wavelengths of familiar electromagnetic radiation range from 101 m for radio waves to 10−12 m for gamma rays, which are emitted by nuclear reactions. Viewing the equation below, we can see how frequency of electromagnetic radiation is inversely proportional to its wavelength:
\[ \begin{array}{cc} c=\lambda \nu \\ \nu =\dfrac{c}{\lambda } \end{array} \label{6.1.2} \]
For example, the frequency of radio waves is about 108 Hz, whereas the frequency of gamma rays is about 1020 Hz. Visible light, which is electromagnetic radiation that can be detected by the human eye, has wavelengths between about 7 × 10−7 m (700 nm, or 4.3 × 1014 Hz) and 4 × 10−7 m (400 nm, or 7.5 × 1014 Hz). Note that when frequency increases, wavelength decreases; c being a constant stays the same. Similarly when frequency decreases, the wavelength increases.
Please memorize equation 5.2.1 and the speed of light (with units). In addition, it is important to know which side of the electromagnetic spectrum is deadly.
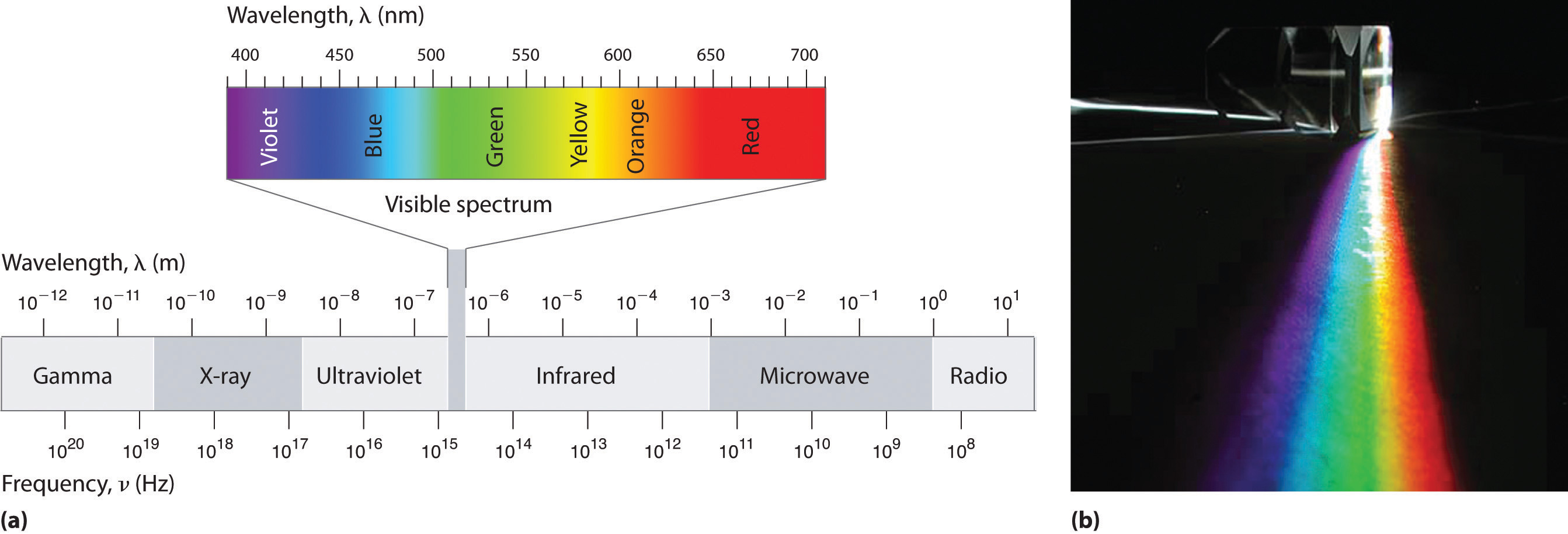
| Unit | Symbol | Wavelength (m) | Type of Radiation |
|---|---|---|---|
| picometer | pm | 10−12 | gamma ray |
| nanometer | nm | 10−9 | x-ray |
| micrometer | μm | 10−6 | infrared |
| millimeter | mm | 10−3 | infrared |
| centimeter | cm | 10−2 | microwave |
| meter | m | 100 | radio |
Light also behaves like a package of energy. It turns out that for light, the energy of the “package” of energy is proportional to its frequency.
\[ E\; \propto\; \nu \label{6.1.3}\]
\[ E\; \propto\; \dfrac{1}{\lambda } \label{6.1.4}\]
Whereas visible light is essentially harmless to our skin, ultraviolet light, with wavelengths of ≤ 400 nm, has enough energy to cause severe damage to our skin in the form of sunburn. Because the ozone layer absorbs sunlight with wavelengths less than 350 nm, it protects us from the damaging effects of highly energetic ultraviolet radiation.
In this course, we will not do energy calculations. You should know the relationship between frequency and energy. Also, you show realize that short wavelength radiation is associated with a high energy.
The energy of electromagnetic radiation increases with increasing frequency and decreasing wavelength.
Example \(\PageIndex{1}\)
What is the frequency of light if its wavelength is 5.55 × 10−7 m?
Solution
We use the equation that relates the wavelength and frequency of light with its speed. We have
\[3.00\times 10^{8}m/s=\left ( 5.55\times 10^{-7} m\right )\nu\]
We divide both sides of the equation by 5.55 × 10−7 m and get
\[\nu =5.41\times 10^{14}s^{-1}\]
Note how the m units cancel, leaving s in the denominator. A unit in a denominator is indicated by a −1 power—s−1—and read as “per second.”
Exercise \(\PageIndex{1}\)
What is the wavelength (in mm) of light if its frequency is 1.55 × 1010 s−1?
- Answer
-
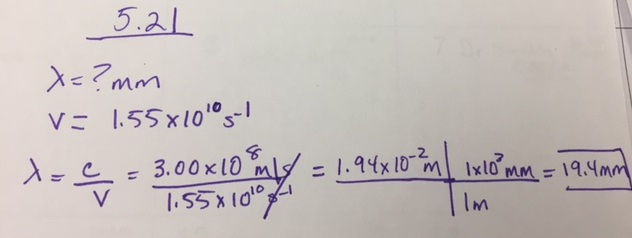
Example \(\PageIndex{2}\)
Calculate the frequency of radiation if its wavelength is 988 nm. Where does this radiation appear in the electromagnetic spectrum?
- Answer
-
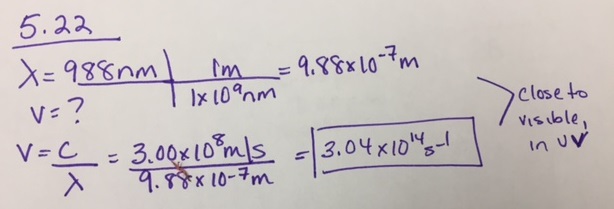
Need More Practice?
- Refer to section 5.E of this OER and work problem #4. Refer to the electromagnetic spectrum to locate the type of radiation.
Contributors
- Emma Gibney (Furman University)


