10.1: The Rate of a Chemical Reaction
- Last updated
- Save as PDF
- Page ID
- 236005
↵
Learning Objectives
- Describe the conditions for successful collisions that cause reactions.
- Describe rate in terms of the conditions of successful collisions.
- Describe how changing the temperature, concentration of a reactant, or surface area of a reaction affects the rate of a reaction.
- Define a catalyst and how a catalyst affects the rate of a reaction.
We know that a chemical system can be made up of atoms (\(\ce{H_2}\), \(\ce{N_2}\), \(\ce{K}\), etc.), ions (\(\ce{NO_3^-}\), \(\ce{Cl^-}\), \(\ce{Na^+}\), etc.), or molecules (\(\ce{H_2O}\), \(\ce{C_{12}H_{22}O_{11}}\), etc.). We also know that in a chemical system, these particles are moving around in random motion. The collision theory explains why reactions occur at this particle level between these atoms, ions, and/or molecules. It also explains how it is possible to speed up or slow down reactions that are occurring.
Collision Theory
The collision theory provides us with the ability to predict what conditions are necessary for a successful reaction to take place. These conditions include:
- The particles must collide with each other.
- The particles must collide with sufficient energy to break the old bonds.
- The particles must have proper orientation.
A chemical reaction involves breaking bonds in the reactants, rearranging the atoms into new groupings (the products), and forming new bonds in the products.
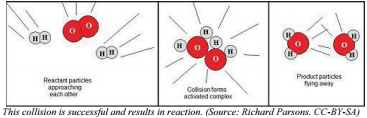
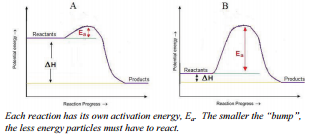
Therefore, a collision must not only occur between reactant particles, but the collision also has to have sufficient energy to break all the reactant bonds that need to be broken in order to form the products. Some reactions need less collision energy than others. The amount of energy that reactant particles must have in order to break the old bonds for a reaction to occur is called the activation energy, abbreviated \(\text{E}_a\). Another way to think of this is to look at an energy diagram, as shown in the figure. Particles must be able to get over the "bump"—the activation energy—if they are going to react. If the reactant particles collide with less than the activation energy, the particles will rebound (bounce off of each other), and no reaction will occur.
Reaction Rate
Chemists use reactions to generate a product for which they have a use. For the most part, the reactions that produce some desired compound are only useful if the reaction occurs at a reasonable rate. For example, using a reaction to produce brake fluid would not be useful if the reaction required 8,000 years to complete the product. Such a reaction would also not be useful if the reaction was so fast that it was explosive. For these reasons, chemists wish to be able to control reaction rates. In some cases, chemists wish to speed up reactions that are too slow or slow down reactions that are too fast. In order to gain any control over reaction rates, we must know the factors that affect reaction rates. Chemists have identified many factors that affect the rate of a reaction.
The rate, or speed, at which a reaction occurs depends on the frequency of successful collisions. Remember, a successful collision occurs when two reactants collide with enough energy and with the right orientation. That means if there is an increase in the number of collisions, an increase in the number of particles that have enough energy to react, and/or an increase in the number of particles with the correct orientation, the rate of reaction will increase.
Effect of Temperature on Rate of Reaction
The rate of reaction was discussed in terms of three factors: collision frequency, the collision energy, and the geometric orientation. Remember that the collision frequency is the number of collisions per second. The collision frequency is dependent, among other factors, on the temperature of the reaction.
When the temperature is increased, the average velocity of the particles is increased. The average kinetic energy of these particles is also increased. The result is that the particles will collide more frequently, because the particles move around faster and will encounter more reactant particles. However, this is only a minor part of the reason why the rate is increased. Just because the particles are colliding more frequently does not mean that the reaction will definitely occur.
The major effect of increasing the temperature is that more of the particles that collide will have the amount of energy needed to have an effective collision. In other words, more particles will have the necessary activation energy.
At room temperature, the hydrogen and oxygen in the atmosphere do not have sufficient energy to attain the activation energy needed to produce water:
\[\ce{O_2} \left( g \right) + \ce{H_2} \left( g \right) \rightarrow \text{No reaction} \nonumber \]
At any one moment in the atmosphere, there are many collisions occurring between these two reactants. But what we find is that water is not formed from the oxygen and hydrogen molecules colliding in the atmosphere, because the activation energy barrier is just too high, and all the collisions are resulting in rebound. When we increase the temperature of the reactants or give them energy in some other way, the molecules have the necessary activation energy and are able to react to produce water:
\[\ce{O_2} \left( g \right) + \ce{H_2} \left( g \right) \rightarrow \ce{H_2O} \left( l \right) \nonumber \]
There are times when the rate of a reaction needs to be slowed down. Lowering the temperature could also be used to decrease the number of collisions that would occur and lowering the temperature would also reduce the kinetic energy available for activation energy. If the particles have insufficient activation energy, the collisions will result in rebound rather than reaction. Using this idea, when the rate of a reaction needs to be lower, keeping the particles from having sufficient activation energy will definitely keep the reaction at a lower rate.
Society uses the effects of temperature on reaction rate every day. Food storage is a prime example of how the temperature effect on reaction rate is utilized by society. Consumers store food in freezers and refrigerators to slow down the processes that cause it to spoil. The decrease in temperature decreases the rate at which food will break down or be broken down by bacteria. In the early years of the 20\(^\text{th}\) century, explorers were fascinated with being the first to reach the South Pole. In order to attempt such a difficult task at a time without most of the technology that we take for granted today, they devised a variety of ways of surviving. One method was to store their food in the snow to be used later during their advances to the pole. On some explorations, they buried so much food that they didn't need to use all of it, and some was left behind. Many years later, when this food was located and thawed, it was found to still be edible.
When milk, for example, is stored in the refrigerator, the molecules in the milk have less energy. This means that while molecules will still collide with other molecules, few of them will react (which means in this case "spoil") because the molecules do not have sufficient energy to overcome the activation energy barrier. The molecules do have energy and are colliding, however, and so, over time, even in the refrigerator, the milk will spoil. Eventually the higher energy molecules will gain the energy needed to react and when enough of these reactions occur, the milk becomes "soured".
However, if that same carton of milk was at room temperature, the milk would react (in other words, "spoil") much more quickly. Most of the molecules would have sufficient energy to overcome the energy barrier at room temperature, and many more collisions would occur. This allows for the milk to spoil in a fairly short amount of time. This is also the reason why most fruits and vegetables ripen in the summer when the temperature is much warmer. You may have experienced this first hand if you have ever bitten into an unripe banana—it was probably sour tasting and might even have felt like biting into a piece of wood! When a banana ripens, numerous reactions occur that produce all the compounds that we expect to taste in a banana. But this can only happen if the temperature is high enough to allow these reactions to make those products.
Effect of Concentration on Rate of Reaction
If you had an enclosed space, like a classroom, and there was one red ball and one green ball flying around the room in random motion, undergoing perfectly elastic collisions with the walls and with each other, in a given amount of time, the balls would collide with each other a certain number of times determined by probability. If you now put two red balls and one green ball in the room under the same conditions, the probability of a collision between a red ball and the green ball would exactly double. The green ball would have twice the chance of encountering a red ball in the same amount of time.
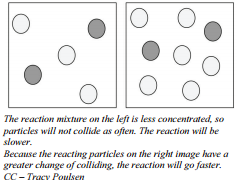 In terms of chemical reactions, a similar situation exists. Particles of two gaseous reactants or two reactants in solution have a certain probability of undergoing collisions with each other in a reaction vessel. If you double the concentration of either reactant, the probability of a collision doubles. The rate of reaction is proportional to the number of collisions per unit time. If one concentration is doubled, the number of collisions will also double. Assuming that the percent of collisions that are successful does not change, then having twice as many collisions will result in twice as many successful collisions. The rate of reaction is proportional to the number of collisions over time; increasing the concentration of either reactant increases the number of collisions, and therefore increases the number of successful collisions and the reaction rate.
In terms of chemical reactions, a similar situation exists. Particles of two gaseous reactants or two reactants in solution have a certain probability of undergoing collisions with each other in a reaction vessel. If you double the concentration of either reactant, the probability of a collision doubles. The rate of reaction is proportional to the number of collisions per unit time. If one concentration is doubled, the number of collisions will also double. Assuming that the percent of collisions that are successful does not change, then having twice as many collisions will result in twice as many successful collisions. The rate of reaction is proportional to the number of collisions over time; increasing the concentration of either reactant increases the number of collisions, and therefore increases the number of successful collisions and the reaction rate.
For example, the chemical test used to identify a gas as oxygen, or not, relies on the fact that increasing the concentration of a reactant increases reaction rate. The reaction we call combustion refers to a reaction in which a flammable substance reacts with oxygen. If we light a wooden splint (a thin splinter of wood) on fire and then blow the fire out, the splint will continue to glow in air for a period of time. If we insert that glowing splint into any gas that does not contain oxygen, the splint will immediately cease to glow—that is, the reaction stops. Oxygen is the only gas that will support combustion, Air is approximately \(20\%\) oxygen gas. If we take that glowing splint and insert it into pure oxygen gas, the reaction will increase its rate by a factor of five, since pure oxygen has 5 times the concentration of oxygen that is in the air. When the reaction occurring on the glowing splint increases its rate by a factor of five, the glowing splint will suddenly burst back into full flame. This test, of thrusting a glowing splint into a gas, is used to identify the gas as oxygen. Only a greater concentration of oxygen than that found in air will cause the glowing splint to burst into flame.
Effect of Surface Area on Rate of Reaction
The very first requirement for a reaction to occur between reactant particles is that the particles must collide with one another. The previous section pointed out how increasing the concentration of the reactants increases reaction rate because it increases the frequency of collisions between particles. It can be shown that the number of collisions that occur between reactant particles is also dependent on the surface area of solid reactants. Consider a reaction between reactant RED and reactant BLUE in which reactant blue is in the form of a single lump. Then compare this to the same reaction where reactant blue has been broken up into many smaller pieces.
 In the diagram, only the blue particles on the outside surface of the lump are available for collision with reactant red. The blue particles on the interior of the lump are protected by the blue particles on the surface. In Figure A, if you count the number of blue particles available for collision, you will find that only 20 blue particles could be struck by a particle of reactant red. In Figure A, there are a number of blue particles on the interior of the lump that cannot be struck. In Figure B, however, the lump has been broken up into smaller pieces and all the interior blue particles are now on a surface and available for collision. In Figure B, more collisions between the blue and red will occur, and therefore, the reaction in Figure B will occur at a faster rate than the same reaction in Figure A. Increasing the surface area of a reactant increases the frequency of collisions and increases the reaction rate.
In the diagram, only the blue particles on the outside surface of the lump are available for collision with reactant red. The blue particles on the interior of the lump are protected by the blue particles on the surface. In Figure A, if you count the number of blue particles available for collision, you will find that only 20 blue particles could be struck by a particle of reactant red. In Figure A, there are a number of blue particles on the interior of the lump that cannot be struck. In Figure B, however, the lump has been broken up into smaller pieces and all the interior blue particles are now on a surface and available for collision. In Figure B, more collisions between the blue and red will occur, and therefore, the reaction in Figure B will occur at a faster rate than the same reaction in Figure A. Increasing the surface area of a reactant increases the frequency of collisions and increases the reaction rate.
Several smaller particles have more surface area than one large particle. The more surface area that is available for particles to collide, the faster the reaction will occur. You can see an example of this in everyday life if you have ever tried to start a fire in the fireplace. If you hold a match up against a large log in an attempt to start the log burning, you will find it to be an unsuccessful effort. Holding a match against a large log will not cause enough reactions to occur in order to keep the fire going by providing sufficient activation energy for further reactions. In order to start a wood fire, it is common to break a log up into many small, thin sticks called kindling. These thinner sticks of wood provide many times the surface area of a single log. The match will successfully cause enough reactions in the kindling so that sufficient heat is given off to provide activation energy for further reactions.
There have been, unfortunately, cases where serious accidents were caused by the failure to understand the relationship between surface area and reaction rate. One such example occurred in flour mills. A grain of wheat is not very flammable. It takes significant effort to get a grain of wheat to burn. If the grain of wheat, however, is pulverized and scattered through the air, only a spark is necessary to cause an explosion. When the wheat is ground to make flour, it is pulverized into a fine powder and some of the powder gets scattered around in the air. A small spark then, is sufficient to start a very rapid reaction which can destroy the entire flour mill. In a 10-year period from 1988 to 1998, there were 129 grain dust explosions in mills in the United States. Efforts are now made in flour mills to have huge fans circulate the air in the mill through filters to remove the majority of the flour dust particles.
Another example is in the operation of coal mines. Coal will of course burn, but it takes an effort to get the coal started; once it is burning, it burns slowly because only the surface particles are available to collide with oxygen particles. The interior particles of coal have to wait until the outer surface of the coal lump burns off before they can collide with oxygen. In coal mines, huge blocks of coal must be broken up before the coal can be brought out of the mine. In the process of breaking up the huge blocks of coal, drills are used to drill into the walls of coal. This drilling produces fine coal dust that mixes into the air; then a spark from a tool can cause a massive explosion in the mine. There are explosions in coal mines for other reasons, but coal dust explosions have contributed to the death of many miners. In modern coal mines, lawn sprinklers are used to spray water through the air in the mine and this reduces the coal dust in the air, and eliminates coal dust explosions.
Effect of a Catalyst on Rate of Reaction
The final factor that affects the rate of the reaction is the effect of a catalyst. A catalyst is a substance that speeds up the rate of the reaction, without being consumed by the reaction itself.
In the reaction of potassium chlorate breaking down to potassium chloride and oxygen, a catalyst is available to make this reaction occur much faster than it would occur by itself under room conditions. The reaction is:
\[2 \ce{KClO_3} \left( s \right) \overset{\ce{MnO_2} \left( s \right)}{\longrightarrow} 2 \ce{KCl} \left( s \right) + 3 \ce{O_2} \left( g \right) \nonumber \]
The catalyst is manganese dioxide and its presence causes the reaction shown above to run many times faster than it occurs without the catalyst. When the reaction has reached completion, the \(\ce{MnO_2}\) can be removed from the reaction vessel and its condition is exactly the same as it was before the reaction. This is part of the definition of a catalyst—that it is not consumed by the reaction. You should note that the catalyst is not written into the equation as a reactant or a product, but is noted above the yields arrow. This is standard notation for the use of a catalyst.
Some reactions occur very slowly without the presence of a catalyst. In other words, the activation energy for these reactions is very high. When the catalyst is added, the activation energy is lowered because the catalyst provides a new reaction pathway with lower activation energy.
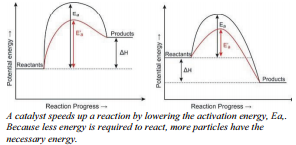 In the figure on the right, the endothermic reaction shows the catalyst reaction in red with the lower activation energy, designated \(\text{E}'_a\). The new reaction pathway has lower activation energy but has no effect on the energy of the reactants, the products, or the value of \(\Delta H\). The same is true for the exothermic reaction. The activation energy of the catalyzed reaction is lower than that of the uncatalyzed reaction. The new reaction pathway provided by the catalyst affects the energy required for reactant bonds to break, and product bonds to form.
In the figure on the right, the endothermic reaction shows the catalyst reaction in red with the lower activation energy, designated \(\text{E}'_a\). The new reaction pathway has lower activation energy but has no effect on the energy of the reactants, the products, or the value of \(\Delta H\). The same is true for the exothermic reaction. The activation energy of the catalyzed reaction is lower than that of the uncatalyzed reaction. The new reaction pathway provided by the catalyst affects the energy required for reactant bonds to break, and product bonds to form.
While many reactions in the laboratory can be increased by increasing the temperature, this is not possible for all of the reactions that occur in our bodies throughout our entire lives. In fact, the body needs to be maintained at a very specific temperature: \(98.6^\text{o} \text{F}\) or \(37^\text{o} \text{C}\). Of course there are times, such as when the body is fighting infection, when the body temperature may be increased. But generally, in a healthy person, the temperature is quite consistent. However, many of the reactions that a healthy body depends on could never occur at body temperature. The answer to this dilemma is catalysts—also referred to as enzymes. Many of these enzymes are made in human cells because human DNA carries the directions to make them. However, there are some enzymes required by the body that are not made by human cells. These catalysts must be supplied to our bodies in the food we eat and are called vitamins.
Reversible Reactions
Typically when we think of a chemical reaction, we think of the reactants getting totally used up so that none are left, and that we end up with only products. Also, we generally consider chemical reactions as one-way events. You may well have learned during earlier science classes that this is one way to distinguish chemical change from physical change—physical changes (such as the melting and freezing of ice) are easily reversed, but chemical changes cannot be reversed (pretty tough to un-fry an egg).
Throughout this chaper, we will see that this isn't always the case. We will see that many chemical reactions are, in fact, reversible under the right conditions. And because many reactions can be reversed, our idea of a reaction ending with no reactants left, only products, will need to be modified.
Here are some examples of reactions that can be reversed:
| 1. |
Nitrogen dioxide, \(\ce{NO_2}\), a reddish-brown gas, reacts to form colorless dinitrogen tetroxide, \(\ce{N_2O_4}\) : \(\ce{2NO_2(g) \rightarrow N_2O_4(g)}\) But the reaction can also go the other way—dinitrogen tetroxide also readily breaks down to form nitrogen dioxide: \(\ce{N_2O_4(g) \rightarrow 2NO_2(g)}\) We typically write a reaction that can go in both directions by using a double arrow (which will sometimes appear as ↔ in these online notes): \(\ce{2NO_2(g) \leftrightarrow N_2O_4(g)}\) Because the reaction continues in both directions at the same time, we never run out of either \(\ce{NO_2}\) or \(\ce{N_2O_4}\) . \(\ce{NO_2}\) is continually being used up to form \(\ce{N_2O_4}\), but at the same time \(\ce{N_2O_4}\) is forming more \(\ce{NO_2}\) |
|---|
| 2. |
When hydrogen gas is passed over heated iron oxide, iron and steam are produced:
When we have a reversible reaction written in this way, we need to be able to distinguish between which way the reaction is headed. As written above in Reaction (3), we would say that in the forward reaction, iron oxide and hydrogen gas, the reactants, produce the products iron and steam. During the reverse reaction, iron reacts with steam to produce the products iron oxide and hydrogen gas. It is important to understand the terminology, and to use the terms correctly. Does it matter which way we write our reversible reaction? It can also be written as \(\ce{3Fe(s) + 4H_2O(g) \leftrightarrow Fe_3O_4(s) + 4H_2(g)}\) Now iron and steam are reactants of the forward direction, and iron oxide and hydrogen gas would be the reactants of the reverse direction. |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
Summary
- The collision theory explains why reactions occur between atoms, ions, and molecules.
- In order for a reaction to be effective, particles must collide with enough energy, and have the correct orientation.
- With an increase in temperature, there is an increase in energy that can be converted into activation energy in a collision, and that will increase the reaction rate. A decrease in temperature would have the opposite effect.
- With an increase in temperature, there is an increase in the number of collisions.
- Increasing the concentration of a reactant increases the frequency of collisions between reactants and will, therefore, increase the reaction rate.
- Increasing the surface area of a reactant (by breaking a solid reactant into smaller particles) increases the number of particles available for collision and will increase the number of collisions between reactants per unit time.
- A catalyst is a substance that speeds up the rate of the reaction without being consumed by the reaction itself. When a catalyst is added, the activation energy is lowered because the catalyst provides a new reaction pathway with lower activation energy.
Vocabulary
- Catalyst - A substance that speeds up the rate of the reaction without being consumed by the reaction itself.
- Surface area to volume ratio - The comparison of the volume inside a solid to the area exposed on the surface.
Further Reading/Supplemental Links
- Activation Energy: http://www.mhhe.com/physsci/chemistr...sh/activa2.swf
- learner.org/resources/series61.html The learner.org website allows users to view streaming videos of the Annenberg series of chemistry videos. You are required to register before you can watch the videos, but there is no charge. The website has one video that relates to this lesson called Molecules in Action.
- www.vitamins-guide.net
- en.Wikipedia.org/wiki
- Observing molecules during chemical reactions helps explain the role of catalysts. Dynamic equilibrium is also demonstrated. Molecules in Action (www.learner.org/vod/vod_window.html?pid=806)
- Surface science examines how surfaces react with each other at the molecular level. On the Surface (www.learner.org/vod/vod_window.html?pid=812)

