27.1: Solid-Liquid Systems - Eutectic Points
- Page ID
- 238683
A phase diagram for two immiscible solids and the liquid phase (which is miscible in all proportions) is shown in Figure \(\PageIndex{1}\). The point labeled “e2” is the eutectic point, meaning the composition for which the mixture of the two solids has the lowest melting point. The four main regions can be described as below:
- Two-phase solid
- Solid (mostly A) and liquid (A and B)
- Solid (mostly B) and liquid (A and B)
- Single phase liquid (A and B)
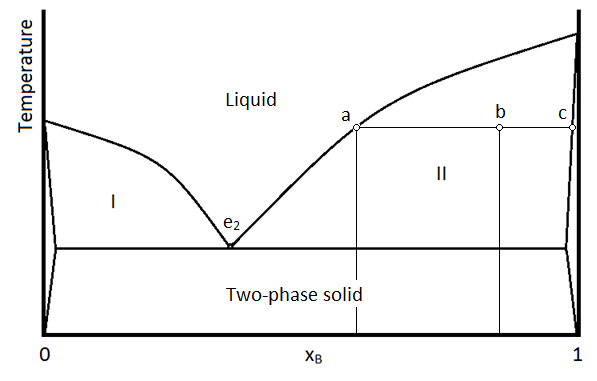
The unlabeled regions on the sides of the diagram indicate regions where one solid is so miscible in the other, that only a single phase solid forms. This is different than the “two-phase solid” region where there are two distinct phases, meaning there are regions (crystals perhaps) that are distinctly A or B, even though they are intermixed within on another. Region I contains two phases: a solid phase that is mostly compound A, and a liquid phase which contains both A and B. A sample in region II (such as the temperature/composition combination depicted by point b) will consist of two phases: 1 is a liquid mixture of A and B with a composition given by that at point a, and the other is a single phase solid that is mostly pure compound B, but with traces of A entrained within it. As always, the lever rule applies in determining the relative amounts of material in the two phases.
In the case where the widths of the small regions on either side of the phase diagram are negligibly small, a simplified diagram with a form similar to that shown in Figure \(\PageIndex{2}\) can be used. In this case, it is assumed that the solids never form a single phase! The tin-lead system exhibits such behavor.

Another important case is that for which the two compounds A and B can react to form a third chemical compound C. If the compound C is stable in the liquid phase (does not decompose upon melting), the phase diagram will look like Figure \(\PageIndex{3}\).
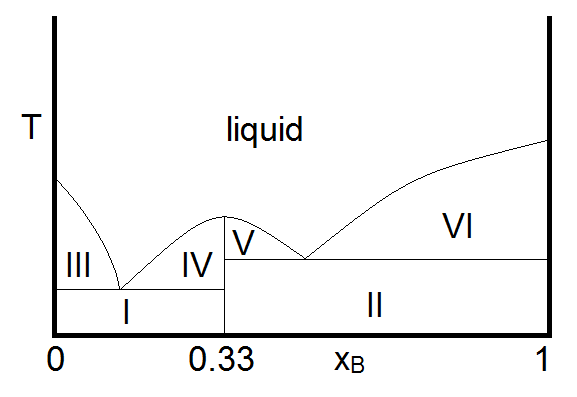
In this diagram, the vertical boundary at \(X_B = 0.33\) is indicative of the compound \(C\) formed by \(A\) and \(B\). From the mole fraction of \(B\), it is evident that the formula of compound \(C\) is \(A_2B\). The reaction that forms compound C is
\[2 A + B \rightarrow C\]
Thus, at overall compositions where \(X_B < 0.33\) , there is excess compound A (B is the limiting reagent) and for \(X_B \) there is an excess of compound \(B\) (\(A\) is now the limiting reagent.) With this in mind, the makeup of the sample in each region can be summarized as
- Two phase solid (A and C)
- Two phase solid (C and B)
- Solid A and liquid (A and C)
- Solid C and liquid (A and C)
- Solid C and liquid (C and B)
- Solid B and liquid (C and B)
- liquid. Single phase liquid (A and C or C and B, depending on which is present in excess)
Zinc and Magnesium are an example of two compounds that demonstrate this kind of behavior, with the third compound having the formula \(Zn_2Mg\) (Ghosh, Mezbahul-Islam, & Medraj, 2011).
Incongruent Melting
Oftentimes, the stable compound formed by two solids is only stable in the solid phase. In other words, it will decompose upon melting. As a result, the phase diagram will take a lightly different form, as is shown in Figure \(\PageIndex{4}\).
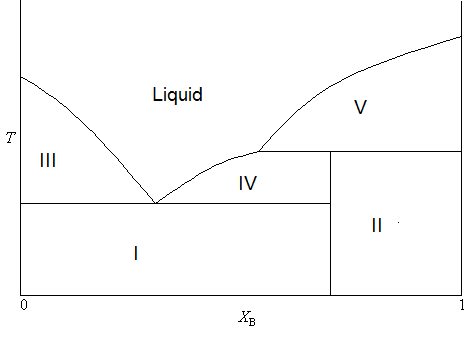
In this diagram, the formula of the stable compound is \(AB_3\) (consistent with \(X_B < 0.75\)). But you will notice that the boundary separating the two two-phase solid regions does not extend all of the way to the single phase liquid portion of the diagram. This is because the compound will decompose upon melting. The process of decomposition upon melting is also called incongruent melting. The makeup of each region can be summarized as
- Two phase solid (A and C)
- Two phase solid (C and B)
- Solid A and liquid (A and B)
- Solid C and liquid (A and B)
- Solid B and liquid (A and B)
There are many examples of pairs of compounds that show this kind of behavior. One combination is sodium and potassium, which form a compound (\(Na_2K\)) that is unstable in the liquid phase and so it melts incongruently (Rossen & Bleiswijk, 1912).
Contributors
Patrick E. Fleming (Department of Chemistry and Biochemistry; California State University, East Bay)


